The Class

5 quizzes (lowest one dropped)

2 midterms

Integration

There are two methods. Don’t think of them as rules.

There are infinitely many integrals that cannot be integrated. For example $\int \frac{e^x}{x} dx$ and $\int \frac{x}{\ln x} dx$.

Substitution

Example (#26):

$\int \sin ^{10} x \cos ^3 (x) dx$

$\int \sin^{10} x \cos ^2 (x) \cos (x) dx$

$\int \sin^{10} x \left( 1-\sin^2(x) \right) \cos (x) dx$

$u = \sin x$

$du = \cos x$

$\int u^{10} (1-u^2) du$

$\int u^{10} dx - \int u^{12} du$

Example:

$\int \frac{\ln x}{x} dx$

Let $z = \ln x$

Then $dz = \frac{1}{x} dx$

$\int z dz = \frac{z^2}{2} = \frac{1}{2} \ln (x)^2 + C$

Example:

$\int \frac{dx}{x-1}$

Let $u = x-1$

$du = dx$

$\int \frac{du}{u} = \ln u + C = \ln (x-1) + C$

Example:

$\int \frac{dx}{2x+1}$

$\frac{1}{2} \int \frac{d(2x)}{2x+1}$

Example:

$\int \frac{dx}{\sqrt{2x+1} } dx$

Let $2x+1 = u$

$du = 2 dx \implies dx = \frac{1}{2} du$

$\frac{1}{2} \int \frac{du}{\sqrt{u} } = \frac{1}{2} \frac{u^{\frac{1}{2}}}{\frac{1}{2}} = \sqrt{2x + 1} + C$

Example:

$\int \frac{\sin^{-1} x}{\sqrt{1-x^2} } dx$

Let $\sin ^{-1} x = u$

$du = \frac{dx}{\sqrt{1+ x^2} }$

$\int d du = \frac{u^2}{2} = \frac{\sin ^{-1} x ^2}{2} + C$

Example:

$\int \frac{tan^{-1} x}{1+x^2} dx$

Example:

$\int x^2 e^{3x^3} dx$

Let $t = 3x^3$

$dt = 9x^2 dx$

$x^2 dx = \frac{1}{9} dt$

$\frac{1}{9} \int e^t dt = \frac{1}{9} e^t = \frac{1}{9} e^{3x^2} + C$

By Parts

Definition: $(u v) ‘ = v * u’ + u * v’$

$\frac{d}{dx}(u v) = v \frac{d}{dx} u + u \frac{d}{dx} v$

$\frac{d(uv)}{dx} = v \frac{du}{dx} + u \frac{dv}{dx}$

$d(uv) = v du + u dv$

$\int d (uv) = \int v du + \int u dv$

$uv = \int v du + \int u dv$

$\int u dv = uv - \int v du$

What should be $u$ and $dv$?

L	Logarithmic Functions
I	Inverse Trigonometric Function
A	Algebraic Functions
T	Trigonometric Functions
E	Exponential Functions

(Not a rule, but is helpful)

Example:

$\int \ln x dx$

$u = \ln x \implies du = \frac{dx}{x}$

$dv = dx \implies v =x$

$\int \ln x dx = x \ln x - \int x \frac{dx }{x} = x \ln x - \int dx = x \ln x - x + C$

Example:

$\int x \ln x dx$

$u = \ln x \implies du = \frac{dx}{x}$

$dv = x dx \implies v = \frac{x^2}{2}$

$= \frac{x^2}{2} \ln x - \frac{1}{2} \int x^2 \frac{dx}{x} = \frac{x^2}{2} \ln x - \frac{1}{2} \ln x dx = \frac{x^2}{2} \ln x - \frac{1}{2} \frac{x^2}{2} = \frac{x^2}{2} \left( \ln x - \frac{1}{2} \right) + C$

Example:

$\int x^2 e^{5x} dx$

$u = x^2 \implies du = 2x dx$

$dv = e^{5x} dx \implies v = \frac{1}{5} e^{5x}$

$\int x^2 e^{5x} dx = \frac{1}{5} x^2 e^{5x} - \frac{2}{5} \int x e^{5x} dx$

Second round:

$u = x \implies du = dx$

$dv = e^{5x} dx \implies v = \frac{1}{5} e^{5x}$

$= \frac{1}{5} x^2 e^{5x} - \frac{2}{5}\left( \frac{1}{5}x^{5x} - \frac{1}{5}\int e^{5x} dx \right)$

$= \frac{1}{5} x^2 e^{5x} - \frac{2}{25}x e^{5x} + \frac{2}{125} e^{5x}$

$= \frac{1}{5} e^{5x} \left( x^2 - 2x + \frac{2}{25} \right) + C$

Example:

$\int x \sin x dx$

$u = x \implies du = dx$

$ dv = \sin x dx \implies v = - \cos x$

$\int x \sin x dx = -x \cos x + \int \cos x dx$

$= - x \cos x + \sin x + C$

First quiz on Wednesday.

Example:

$\int \frac{\ln x}{x} dx$

$u = \ln x \implies du = \frac{dx}{x}$

$dv =\frac{dx}{x} \implies v = \ln x$

$I = \int \frac{\ln x}{x} dx = \left( \ln x \right)^2 - \int \frac{\ln x}{x} dx$

Solve for I

$2I = \left( \ln x \right) ^{2}$

$\therefore I = \frac{1}{2} \left( \ln x \right) ^2 + C$

Example:

$\int e^x \sin x dx$

$u = e^{x} \implies du = d^x dx$

$dv = \sin x dx \implies v = -\cos x$

$\int e^x \sin x dx = -ex \cos x + \int e^x \cos x dx$

Lets do this again. When you do it again, stick to your choice of u and dv (otherwise, you will be left with the $\int e^x \sin x dx = \int e^x \sin x dx$).

$u = e^x \implies du = e^x dx$

$dv = \cos x dx \implies v = \sin x dx$

$= -e^x \cos x + \left( e^x \sin x - \int e^x \sin x dx \right)$

$= e^x \sin x - e^x \cos x - \int e^x \sin x dx$

$I = e^x \sin x - e^x \cos x - I$

$\therefore I = \frac{1}{2} e^x \left( \sin x - \cos x \right) + C$

Example (on your own):

$\int e^{2x} \cos \frac{x}{3} dx$

Example:

$\int \frac{\ln x}{x^2} dx$

We can do this both by subtitiution and by parts

By Parts:

$u = \ln x \implies du = \frac{dx}{x}$

$dv = \frac{dx}{x^3} \implies v= -\frac{1}{2x^2}$

$\int \frac{\ln x}{x^2} dx = -\frac{1}{2x^2} \ln x + \frac{1}{2} \int \frac{dx}{x^3}$

By Substitution:

$- \int \frac{\ln \frac{1}{x}}{x^2} dx$

Let $u = \frac{1}{x} \implies du = -\frac{dx}{x^2}$

$= - \int u \ln u du$

You can do the rest by parts

Example:

• Do not pay attention to constants – they are irrelevant!
• We only care about the structure

$\int x e^{x^2} dx$ By Substitution Example:

$\int x^2 e^x dx$ By parts Example:

$u = x^2 \implies du = 2x dx$

$dv = e^x dx \implies v = e^x$

Example: $\int x^2 e^{x^2} dx$ By Parts (do on your own)

Example: $\int t^n e^t dt$

$u = t^n \implies du = ut^{u-1}$

$dv = e^t dt \implies v = e^t$

$= t^n e^t - u \int t^{u-1} e^t dt$

This is valid for all $n \ge 0$

Example:

$\int \sin ^n x dx = \int \sin^{n-1} x \sin x dx$

$u = \sin^{n-1} x \implies du = \left( n-1 \right) \sin^{n-2} x * \cos x$

$dv = \sin x dx \implies v = - \cos x$

$=-\cos x \sin^{n-1} x + \left( n-1 \right) \int \cos ^2 x \sin ^{n-2} x dx$

$=-\cos x \sin^{n-1} x + \left( n-1 \right) \left( \int \sin ^{n-2} x dx - \int \sin^u x dx \right)$

$I =- \cos x \sin^{n-1} x + \left( u-1 \right) \int \sin^{n-2} x dx - n-1) - I$

$\left( 1+ \left( n-1 \right) \right) I = n I =-\cos x \sin^{n-1} x + \left( n+1 \right) \int \sin^{n-2} x dx$

$I = -\frac{1}{n} \cos x \sin^{n-1} x + \frac{n-1}{n} \int \sin ^{n-2} x dx$ for all $n \ge 1$

Let’s now do this the traditional way

Recall $\cos^2 + \sin^2 x = 1$ and $\cos^2 x - \sin^2 x = \cos 2x$

$\int \sin^2 x dx = \frac{1}{2} \int \left( 1-\cos(2x) \right) dx$

$\int \sin^2 x dx = \frac{1}{2} x -\frac{1}{4} \sin 2x + C$

Example:

$\int \frac{\cos x \sqrt{x} }{\sqrt{x} } dx$

$u = \sqrt{x}$

$du = \frac{1}{2\sqrt{x}}$

Example:

$\int \frac{\sin \sqrt{x}}{\sqrt{x} } dx$

Substitute $z= \sqrt{x} \implies dz = \frac{1}{2\sqrt{x} } dx$

$= 2 \int \sin z dz$

$= - 2 \cos \sqrt{x} + C$

Example:

$\int \frac{x\cos\sqrt{1-2x} }{\sqrt{1-x^2} } dx$

Integration by Partial Fraction

$\frac{P(x)}{Q(x)}$, where both $P(x)$ and $Q(x)$ are polynomials. Such that $\deg [Q(x)] > \deg [P(x)]$ ($\deg$ means the degree)

There are four distinct cases:

Case 1:

$Q(x)$ is a product of distinct linear factors

$Q(x) = (x+b_1)(x+b_2) … (x+b_u)$

Then, $\frac{P(x)}{Q(x)} = \frac{A_1}{x+b_1} + \frac{A_2}{x+b_2} + … + \frac{A_u}{x+b_u}$ where $A_1,\ A_2,\ …,\ A_u$ to be found.

Example:

$\frac{x^2 + 2x - 1}{x(2x-1)(x+2)} = \frac{A}{x} + \frac{B}{2x-1} + \frac{C}{x+2}$

$x^2 + 2x - 1 = A(2x-1)(x+2) + Bx (x+2) + Cx(2x-1)$

And solve for A, B, and C.

Case 2:

$Q(x)$ is a product of linear factor, some of which are repeated.

That is, $Q(x)$ has $x+b$ repeated $r$ times i.e. $\left( x+b \right) ^r$

Example:

$\frac{x^3 - x + 1}{(x+1)x^2 (x-1)^3} = \frac{A}{x+1}+ \frac{B}{x} + \frac{C}{x^2} + \frac{D}{x-1} + \frac{E}{(x-1)^2} + \frac{F}{(x-1)^3}$

Case 3:

$Q(x)$ contains irreducible quadratic factors (none of which are repeated). That is, $Q(x)$ has factors $ax^2+bx+c$, where $b^2-4ac <0$ (that is, we have no real roots).

Example:

$\frac{x^3+1}{(x-2)(x^2+1)(x^2+x+4)} = \frac{A}{x-2} + \frac{Bx+C}{x^2+1} + \frac{Dx+E}{x^2+x+4}$

Case 4:

$Q(x)$ has some repeated irreducible quadratic factors. That is $(ax^2+bx+c)^r$.

Example:

$\frac{x^3+x^2+1}{x(x-1)(x^2+x+1)(x^2+1)^3} = \frac{A}{x} + \frac{B}{x-1} + \frac{Cx+D}{x^2+x+1} + \frac{Ex+F}{x^2 + 1} + \frac{Gx+H}{(x^2+1)^2} + \frac{Ix+J}{(x^2+1)^3}$

Example:

$\frac{1}{x^6 - x^3}= \frac{1}{x^3(x^3-1)} = \frac{1}{x^3(x-1)(x^2+x+1)}$

$= \frac{A}{x} + \frac{B}{x^2} + \frac{C}{x^3} + \frac{D}{x-1} + \frac{Ex+F}{x^2+x+1}$

Example:

$\frac{1}{x+x^4} = \frac{1}{x(1-x^3)} = \frac{1}{x(1-x)(1+x+x^2)}$

$=\frac{A}{x} + \frac{B}{1-x} + \frac{Cx+D}{1+x+x^2}$

Example:

$\frac{x^2+1}{(x-1)^2(2x^2+1)(3x^2+2x+1)^3}$

$= \frac{A}{x-1} + \frac{B}{(x-1)^2} + \frac{Cx+D}{2x^2+1} + \frac{Ex+F}{3x^2+2x+1} + \frac{Gx+H}{(3x^2+2x+1)^2} + \frac{Ix+J}{(3x^2+2x+1)^3}$

$\frac{x^2-1}{(x-1)(x^2+2x+2)} = \frac{A}{x-1} + \frac{Bx+C}{x^2+2x+2}$

Full Solution Example (#68 on handout): Expect this kind of question on the final

$\int \frac{10}{(x+1)(x^2+4)} dx$

$\frac{1}{(x+1)(x^2+4)} = \frac{A}{x+1} + \frac{Bx+C}{x^2+4}$

$10 = A(x^2+4) + (x+1)(Bx+C) = Ax^2 + 4A + Bx^2 + Cx + Bx + C$

$0 = A+B \implies A=-B$

$0=C+B \implies C+B=0$

$10 = 4A+C \implies C-4B=10$

$A=2$

$C=-B=2$

$B=-2$

$\int \frac{2}{x+1} dx + \int \frac{-2x+2}{x^2+4} dx$ (substitution)

$= 2 \ln (x+1) - 2 \left( \int \frac{x dx}{4+x^2}- \int \frac{dx}{4+x^2} \right)$

$= 2 \ln (x+1) - 2 \left( \int \frac{x dx}{4+x^2}- \frac{1}{4} \int \frac{dx}{1+\left( \frac{x}{2} \right) ^2} \right)$

$= 2 \ln (x+1) - \ln u + \tan^{-1} \left( \frac{x}{2} \right)$

$= 2 \ln (x+1) - \ln (4+x^2) + \tan ^{-1} \left( \frac{x}{2} \right) + C$

For another example, do #71 on handout.

Example:

$\int \frac{3x^2-2x+3}{x(x^2+1)}$

$\frac{3x^2-2x+3}{x(x^2+1) = \frac{A}{x}+ \frac{Bx+C}{x^2}}$

$3x^2 - 2x + 3 = Ax^2 + A + Bx^2 + Cx$

$3=A+B \implies B = 0$

$C=-2$

$A=3$

$= \int \frac{3}{x} dx + \int -\frac{2}{x^2+1} dx$

$= 3 \ln x - 2 \tan^{-1}(x) dx$

You don’t always have to jump to partial fractions, however. Here is an example:

$\int \frac{dx}{x^4-x} dx = \int \frac{dx}{x(x^3-1)}$

$= \int \frac{dx}{x(x-1)(x^2+x+1)} dx$

$\frac{1}{x(x-1)(x^2+x+1)} = \frac{A}{x}+\frac{B}{x-1}+\frac{Cx+D}{x^2+x+1}$

$1 = A(x-1)(x^2-1)(x^2+x+1) + Bx(x^2+x+1) + (Cx+D)\left( x \right) (x-1)$

$1 = Ax^3 - A + Bx^3 + Bx^2 + Bx + (Cx^2 + Dx)(x-1)$

$1 = Ax^3 - A + Bx^3 + Bx^2 + Bx + Cx^3-Cx^2+Dx^2-Dx$

$0 = A+B+C \implies B+C=1$

$0 = B-C+D \implies B-C+D=0$

$0 = B-D \implies B=D$

$1 = -A \implies A=-1$

$B = \frac{1}{3}$

$D = \frac{1}{3}$

$C = \frac{2}{3}$

$= -\ln x + \frac{1}{3} \ln (x-1) + \int \frac{\frac{2}{3}x + \frac{1}{3}}{x^2+x+1} dx$

$= -\ln x + \frac{1}{3} \ln (x-1) + \frac{1}{3}\int \frac{2x + 1}{x^2+x+1} dx$

In this case, $2x+1$ cancels with substitution. However, if this isn’t the case, you would need to complete the square.

$= - \ln x + \frac{1}{3} \ln (x-1) + \frac{1}{3} \ln (x^2+x+1)$

$= \frac{1}{3} \ln (x^3 - 1) - \frac{1}{3} x^3$

$= \frac{1}{3} \ln \frac{x^3-1}{x^3}$

Example:

$\int \frac{dx}{x^4 - x}= \int \frac{dx}{x^4 \left( 1-\frac{1}{x^3} \right) }$

Let $z = 1- \frac{1}{x^3}$

$dz = \frac{3}{x^3} dx$

$= \frac{1}{3} \int \frac{dz}{z}$

$= \frac{1}{3} \ln \left( \frac{x^3-1}{x^3} \right)$

Example:

$\int \frac{x+1}{(x-2)(x^2+3)} dx$

$\frac{x+1}{(x-2)(x^2+3)} = \frac{A}{x-1}+\frac{Bx+C}{x^2+3}$

$x+1 = Ax^2 + 3A + Bx^2 - Bx + Cx - C$

$0 = A+B \implies A=-B \implies A=\frac{1}{2},\ B=-\frac{1}{2}$

$1 = -B + C$

$1 = 3A- C \implies C = 1-A = \frac{1}{2}$

$I = \frac{1}{2} \int \frac{dx}{x-1} + \int \frac{-\frac{1}{2}x+\frac{1}{2}}{x^2+3} dx$

$I = \frac{1}{2} \ln (x-1) - \frac{1}{2} \int \frac{x-1}{x^2+3} dx$

$I = \frac{1}{2} \ln (x-1) - \frac{1}{2} \left( \int \frac{x}{3+x^2}dx - \int \frac{dx}{3+x^2} \right)$

$I = \frac{1}{2} \ln (x-1) - \frac{1}{2} \left( \int \frac{x}{3+x^2}dx - \frac{1}{3}\int \frac{dx}{1+\left( \frac{x}{\sqrt{3} } \right) ^2} \right)$

Now do substitution with both integrals ($u = x^2+3$ and $z = \frac{x}{\sqrt{3} }$ respectively)

$\frac{1}{2} \ln (x-1) - \frac{1}{4} \ln (3+x^2) + \frac{1}{2\sqrt{3} } \tan ^{-1} \left( \frac{x}{\sqrt{3} } \right) +C$

Example

$\int \frac{e^{\frac{1}{x}}}{x^3} dx$

$z = \frac{1}{x} \implies dz = -\frac{1}{x^2} dx$

$\int z e^z (-dz)$

$u = e^{\frac{1}{x}} \implies du = e^{\frac{1}{x}} \left( -\frac{1}{x^2} dx \right)$

$dv = \frac{dx}{x^3} \implies v = -\frac{1}{2} x^{-2}$

$-\frac{1}{2} x^{-2} e^{\frac{1}{x}} + \int \frac{1}{2}x^{-2} e^{\frac{1}{x}} \left( \frac{1}{x^2} dx\right)$

DNF

Improper Integrals

$\int_{1}^{3} \frac{dx}{x} = \ln x \mid _{-1}^{3}$

We cannot do this because you cannot do a log of a negative number.

This makes sense because we cannot divide by zero (in the integral).

$\int_{0}^{\infty} e^x dx$

Type 1: Infinite Integrals

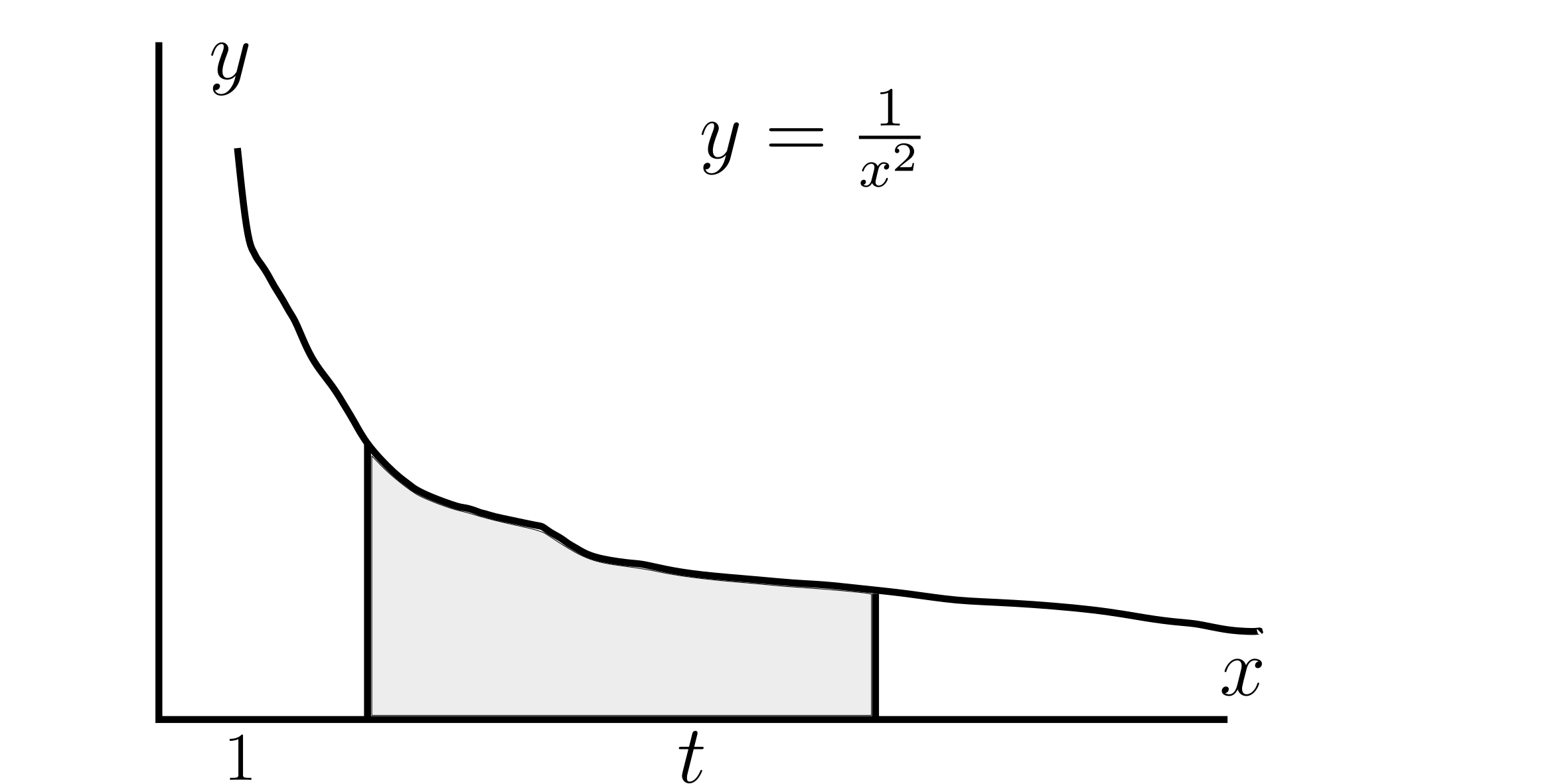
Consider infinite region under $g=\frac{1}{x^2}$ above x-axis and to the right from the line $x$.

$\int_{1}^{\infty} \frac{1}{x^2}dx$

To evaluate this integral, we use the following:

$\int_{1}^{\infty} \frac{Ax}{x^2} = \lim_{t \to \infty} \int_{1}^{t} \frac{dx}{x^2}$

$= \lim_{t \to \infty} \left( -\frac{1}{x} \right) \mid _{1}^{t}$

$=\lim_{t \to \infty} - \frac{1}{t} + \frac{1}{1} = 1$

This converges to 1.

The improper integral $\int_{a}^{\infty} f(x) dx$ and $\int_{-\infty}^{b} f(x) dx$ are called convergent if the corresponding limits exists as finite number and divergent if the limit does not exist.

$\int_{-\infty}^{\infty} f(x) dx = \int_{-\infty}^{a} f(x) dx + \int_{a}^{\infty} f(x) dx$

(Usually $a=0$) which brings two cases (a) and (b). If any of them are divergent, then $\int_{-\infty}^{\infty} f(x) dx$ is divergent.

Example:

$\int_{0}^{\infty} \tan^{-1} x dx$

Zero is okay, but $\infty$ is not.

Example:

Determine the convergence and divergence

$\int_{1}^{\infty} \frac{dx}{x}$ this is divergent (but any power greater than 1 is convergent)

$\lim_{t \to \infty} \int_{1}^{t} \frac{dx}{x}$

$= \lim_{t \to \infty} \ln t - \ln 1 = \infty$ diverges

Example:

$\int_{-\infty}^{0} xe^x dx = \lim_{a \to -\infty} \int_{a}^{0} xe^x dx$

$\int xe^x dx$

$u = x \implies du = dx$

$dv = e^x dx \implies v=e^x$

$\int xe^x dx = xe^x - \int e^x dx = xe^x - e^x$

$= \lim_{a \to -\infty} \left( xe^x - e^x \right) \mid _{a}^{0}$

$= \lim_{a \to \infty} \left( -1 - \left( ae^a - e^a \right) \right)$

$= \lim_{a \to \infty} [e^a - ae^a - 1]$

L’Hopital’s Rule:

$= \lim_{a \to \infty} [e^a - \frac{a}{e^{-a}} - 1]$

$= \lim_{a \to \infty} [e^a - \frac{1}{e^{-a} \times -1} - 1]$

$= \lim_{a \to \infty} [0 - 0 - 1] = -1$ converges

Example:

$\int_{-\infty}^{\infty} \frac{1}{1+x^2}dx$

$\int_{-\infty}^{0} \frac{1}{1+x^2} dx + \int_{0}^{\infty} \frac{1}{1+x^2} dx$

$= \lim_{t \to -\infty} \tan^{-1} x \mid {t}^{0} + \lim{z \to \infty} \tan^{-1} x \mid_{0}^{z}$

$= \frac{\pi}{2} + \frac{\pi}{2} = \pi$

Example:

For what values of $b$ is the integral $\int_{1}^{\infty} \frac{dx}{x^p}$?

Recall that $\int_{1}^{\infty} \frac{dx}{x^2} = 1$

And that $\int_{1}^{\infty} \frac{dx}{x} = \infty$ so it diverges.

So now we have to investigate $p>1$ and $p<1$. Lets consider the case when $p>1$.

$\int_{1}^{\infty} \frac{dx}{x^p} = \lim_{b \to \infty} \int_{1}^{b} \frac{dx}{x^p} = \lim_{b \to \infty} \frac{x^{-p+1}}{-p+1} \mid _{1}^{b}$

$= \frac{1}{1-p} \lim_{b \to \infty} x^{1-p} \mid _{1}^{b}$

$= \frac{1}{1-p} \lim_{b \to \infty} \left( \frac{1}{b^{p-1}}-1 \right)$

Now consider when $p>1$. In that case, $p-1>0$ and $b^{p-1}$ goes to $\infty$ if $b$ goes to $\infty$ and therefore converges to $\frac{1}{p-1}$.

Now, what happens when $p<1$? In that case, $\frac{1}{b^{p-1}}$ goes to $\infty$ as $b$ goes to $\infty$ and the integral diverges.

Type 2: Discontinuous Integrands

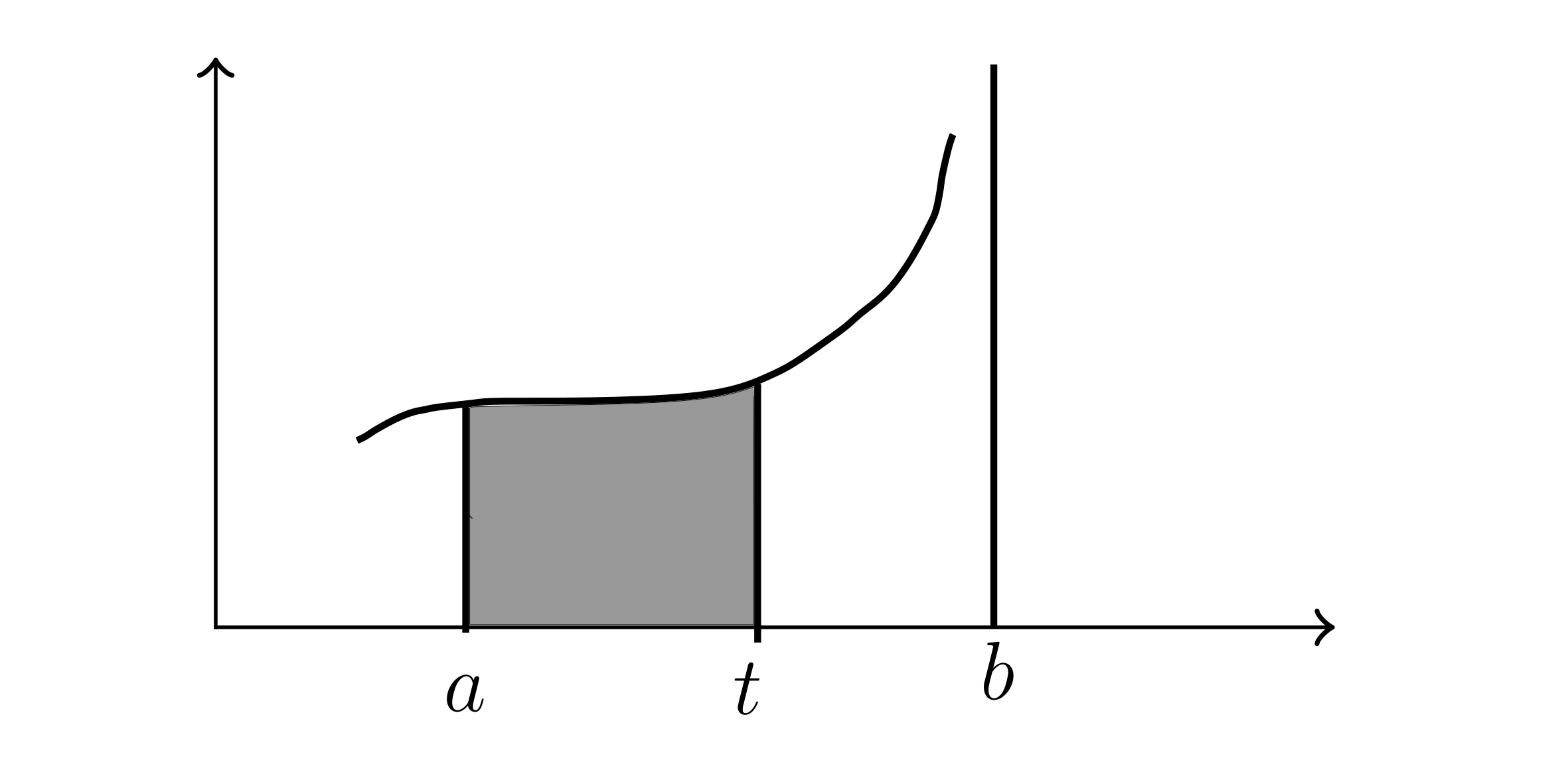
Let $f(x)$ be continuous positive on $[a,\ b]$ (i.e has disc).

At $x=b$ let $S$ be the unbounded region. The shaded area between $a$ and $t$ is $A(t) = \int_{a}^{t} f(x) dx$

If $A(t)$ approaches some definite number $A$ as $t$ goes to $b^{-}$ (approaches from the negative), then the area of the region $S$ is $A$ and write:

$\int_{a}^{b} f(x) dx = \lim_{t \to b^{-}} \int_{a}^{t} f(x) dx$

Case a:

$f(x)$ is continuous on $[a,\ b]$ and discontinuous at $a=b$, then $\int_{a}^{b} f(x) dx = \lim_{t \to b^{-}} \int_{a}^{t} f(x) dx$

Case b:

$f(x)$ is continuous on $[a,\ b]$ and discontinuous at $x=a$.

$\int_{a}^{b} f(x) dx = \lim_{t \to a^{+}} \int_{t}^{b} f(x) dx$

Case c:

$f(x)$ is continuous on $[a,\ b]$ and discontinuous at $x=c$, where $a<c<b$.

$\int_{a}^{b} f(x) dx = \int_{a}^{c} f(x) dx + \int_{c}^{b} f(x) dx$

$= \lim_{t \to c^{-}} \int_{a}^{t} f(x) dx + \lim_{t \to c^+} \int_{t}^{b} f(x) dx$

Example:

Find $\int_{2}^{5} \frac{dx}{x-2} = \lim_{t \to 2^+} \int_{t}^{5} \frac{dx}{\sqrt{x-2}}$

$\lim_{t \to 2^+} \int_{t}^{5} \frac{d(x-2)}{\sqrt{x-2}} = \lim_{t \to 2^+} \frac{(x-2)^{\frac{1}{2}}}{\frac{1}{2}} \mid _{t}^{5}$

$= 2 \lim_{t \to 2^+} \left( 3^{\frac{1}{2}} - (t-2)^{\frac{1}{2}} \right) = 2\sqrt{3}$ converges!

---

$\int_{0}^{\frac{\pi}{2}} \sec x dx = \int_{0}^{\frac{\pi}{2}} \frac{1}{\cos x} dx$

$= \lim_{t \to \frac{\pi}{2}} \int_{0}^{t} \frac{dx}{\cos x}$

$= \lim_{t \to \frac{\pi}{2}} \ln \left( \frac{1}{\cos x}+ \tan x \right) \mid _{0}^t$

$= \lim_{t \to \left( \frac{\pi}{2} \right) ^-} \left( \ln \left( \frac{1}{\cos t} + \frac{\sin t}{\cos t} \right) - \ln 1 \right)$

$= \infty$ therefore it diverges

$\int \frac{dx}{\cos x} = \int \frac{\cos x dx}{\cos ^2 x} = \int \frac{\cos x dx}{1 - \sin x}$

Let $z = \sin x \implies dz = \cos x dx$

$= \int \frac{dz}{1-z^2} = \int \frac{dz}{(1-z)(1+z)} = \frac{1}{2} \int \left( \frac{1}{1-z}+ \frac{1}{1+z} \right) dz$

$= \frac{1}{2} \left( \ln (1+z) - \ln (1-z) \right) = \frac{1}{2} \ln \left( \frac{1+z}{1-z} \right)$

$\frac{1}{2} \ln \left( \frac{1+\sin x}{1-\sin x} \right)$

$= \frac{1}{2} \ln \left( \frac{\left( 1+\sin x \right) ^2}{\cos ^2 x} \right)$

$= \ln \left( \sec x + \tan x \right)$

Example:

$\int_{0}^{3} \frac{dx}{x-1} = \int_{0}^{1} \frac{dx}{x-1} + \int_{1}^{3} \frac{dx}{x-1}$

Doing the first part:

$\int_{0}^{1} \frac{dx}{x-1} = \lim_{t \to 1^-} \int_{0}^{t} \frac{dx}{x-1}$

$= \lim_{t \to 1^-} \ln (x-1) \mid {0}^{t} = \lim{t \to 1^-} \left( \ln \mid t-1 \mid - \ln \mid -1 \mid \right) = - \infty$ Diverges!

Don’t need to check the other one, because if one diverges, the entire integral diverges.

So $\int_{0}^{3} \frac{dx}{x-1}$ diverges!

Be careful! Just solving the integral doesn’t work. You have to handle improper integral.

Example:

$\int_{0}^{1} \ln x dx = \lim_{z \to 0^+} \int_{z}^{1} \ln x dx$ (can only do this integral by parts)

Recall that $\int \ln x dx = \int 2 \ln x - x$

$= \lim_{z \to 0^+} \left( x \ln x - x \right) \mid {z}^1 = \lim{z \to 0^+} \left( \left( 0-1 \right) - \left( z \ln z - z \right) \right)$

$= \lim_{z \to 0^+} \left( 0-z \ln z - 1 \right)$ This is $o \times \infty$ so we need to use L’Hopital’s rule

$z \ln z = \frac{\ln z}{\left( \frac{1}{z} \right) } =L’= \frac{\frac{1}{z}}{\frac{-1}{z^2}} = -z$

$= -1$

The geometric representation of the result asymptotically goes to -1.

Example:

$\int_{1}^{\infty} \frac{dy}{\left( 4y-3 \right)^{\frac{1}{2}}}$

Let $z = 4y-3 \implies dz = 4 dy$

$\frac{1}{4} \int_{1}^{\infty} \frac{dz}{\sqrt{z}} = \frac{1}{2} \sqrt{z} = \frac{1}{2} \sqrt{4y-3}$

$= \lim_{t \to \infty} \frac{1}{2} \sqrt{4y-3} \mid {1}^{t} = \frac{1}{2} \lim{t \to \infty} \left( \sqrt{4t+3} -1 \right) = \infty$ Diverges!

Example:

$\int_{0}^{1} \frac{dt}{\sqrt{1-t ^{2}}}= \lim_{z \to 1^-} \int_{0}^{z} \frac{dt}{\sqrt{1-t^2}}$

$= \lim_{z \to 1^-} \sin^{-1} t \mid {0}^z = \lim{z \to 1^-} \left( \sin^{-1} z - 0 \right)$

$\lim_{z \to 1^{-1}} \sin ^{-1} z = \frac{\pi}{2}$ Converges

$t= \sin \alpha \implies dt \cos \alpha d \alpha$

$\int \frac{\cos \alpha d \alpha}{\sqrt{1- \sin^2 \alpha}} = \int \frac{\cos \alpha d\alpha}{\cos \alpha} = \sin ^{-1} t$

What if we say $t = \cos \alpha$?

$\int \frac{-\sin \alpha d\alpha}{\sqrt{1-\cos^2 \alpha}} = - \int \frac{\sin ^2 \alpha d \alpha}{\sin \alpha} = - \int d \alpha = -\alpha = -\cos ^{-1} t + C$

$\sin ^{-1} t + \cos ^{-1} t = \frac{\pi}{2}$

$\sin ^{-1} t = \frac{\pi}{2} - \cos ^{-1} t$

Next quiz tomorrow:

• Improper integrals

Numerical Integration

Trapezoidal Rule

n - number of rectangles

$\int_{a}^{b} f(x) dx = ?$ Numerical Approximation of this Definite Integral

$T_n = \frac{R_n + L_n}{2}$ This is the trapezoidal rule.

This means that if $n=4$ then you will have 5 terms.

For k number of rectangles:

$L_k = \Delta x \left( f(x_1) + f(x_2) + … + f(x_{k-2}) + f(x_{k-1}) \right)$

$R_k = \Delta x \left( f(x_2) + f(x_3) + … + f(x_{k-2}) + f(x_{k-1}) + f(x_k) \right)$

Example:

$\int_{0}^{2} e^x dx = e^x \mid _{0}^2 = e^2 - e^0 = e^2 - 1 \approx 6.389056$

For $n=4$:

$\Delta x = \frac{b-a}{n} = \frac{2-0}{4} = \frac{1}{2}$

$T_4 = \frac{\Delta x}{2} \left( f(x_1) + 2f(x_2)+2f(x_3) + 2f(x_4) + f(x_5) \right)$

$= \frac{1}{4} \left( f(0) + 2f(\frac{1}{2}) + 2f(1) + 2f\left( \frac{3}{2} \right) +f(2) \right)$

$= \frac{1}{4} \left( 1+2e^{0.5} + 2e + 2e^{1.5} + e^2 \right)$

$\approx 6.52161$

Simpsons Rule

• Going to be on the midterm and final (trapezoidal rule is not)

For $n=2$:

$\int_{a}^{b} f(x) dx \approx \frac{\Delta x}{3}\left( f(x_1)+4f(x_2)+f(x_3) \right)$

For $n=4$:

$\int_{a}^{b} f(x) dx \approx \frac{\Delta x}{3} \left( f(x_1)+4f(x_2)+2f(x_3)+4f(x_4)+f(x_5) \right)$

For $n=6$

$\int_{a}^{b} f(x) dx \approx \frac{\Delta x}{3} \left( f(x_1) + 4f(x_2) + 2f(x_3) + 4f(x_4) + 2f(x_5) + 4f(x_6) + f(x_7) \right)$

Example:

$\int_{0}^{2} e^x dx = e^x \mid _{0}^2 = e^2 - e^0 = e^2 - 1 \approx 6.389056$

For $n=4$:

$S_4 = \frac{\Delta x}{3}\left( f(x_1) + 4f(x_2) + 2f(x_3) + 4f(x_4) + f(x_5) \right)$

$\frac{1}{6} \left( f(0) + 4f(0.5) + 2f(1) + 4f(1.5) + f(2) \right)$

$= \frac{1}{6} \left( 1+4e^{0.5} + 2e + 4e^{1.5}+e^2 \right)$

$\approx 6.39121$ (much better than the trapezoidal approximation)

Any polynomial of a third degree gives the exact integral.

$\int_{1}^{3} \left( x^3 + x-1 \right) dx = \left( \frac{x^4}{4}+\frac{x^{2}}{2}-x \right) \mid _{1}^3 = 22$

$\Delta x = \frac{1}{2}$

$S_4 = \frac{\Delta x}{3} \left( f(x_1) + 4f(x_2) + 2f(x_3) + 4f(x_4) + f(x_5) \right)$

$S_4 = \frac{1}{6} \left( f(1) + 4f(1.5) + 2f(2) + 4f(2.5) + f(3) \right) = 22$

Example:

$\int_{0}^{1} \frac{dy}{1+y^2} = \frac{\pi}{4}$

Try with $n=6$.

Rectilinear Motion

Vectors: have both magnitude and direction

• Can be negative (which means the opposite direction)

Scalers: just have magnitude

• Only positive

Distance is always $= \int_{a}^{b} \mid \vec{v}(t) \mid dt = \int_{a}^{b} \sqrt{f_1^2 (t) + f _2^2(t) + f _3^2 (t)} dx$

Direction is a scaler and displacement is a vector.

Consider a spring that does not deform. If you pull it down and let it oscillate, eventually it will reach the starting point and stop. At that time, the displacement is 0, but the distance is not.

$S = \int_{a}^{b} v(t) dt$

We need to solve for $v(t) = 0$. Say $t=c$ is the solution.

On the time interval, there is some instance $t=c$, when the object has $v=0$, i.e. returns (change its direction). Therefore, we write:

$\text{Total Distance} = \mid \int_{a}^{c} v(t) dt \mid + \mid \int_{c}^{b} v(t) dt \mid$

One of these is going to be negative. So we need to pick a point on $a \le t<c$ ($p_1$) and $c<t\le b$ ($p_2$).

If $v(p_1) > 0$, then it moves in positive

If $v(p_2) < 0$, then it moves in negative.

(Or you can just take the absolute value of both)

Example:

$v(t) = \cos t e^{\sin t}$ from $t=0$ to $t=\pi$

Find displacement:

$\text{Displacement} = \int_{0}^{\pi} \cos t e^{\sin t} dt = e^{\sin t} \mid _{0}^{\pi}$

$\int e^{u}du = e^{u}$

$= e^{\sin \pi} - e^{\sin 0} = e^{-1} - 1 = \frac{1}{e} - 1$

Displacement is always less than or equal to distance.

Distance: $= \mid \int_{0}^{\frac{\pi}{2}} \cos t e^{\sin t} dt \mid + \mid \int_{\frac{\pi}{2}}^{\pi} \cos t e^{\sin t} dt \mid$

$= \mid e^{\sin t} \mid _{0}^{\frac{\pi}{2}} \mid + \mid e^{\sin t} \mid _{\frac{\pi}{2}}^{\pi} \mid$

$= \mid e^{\sin \frac{\pi}{2}} - e^{ \sin 0} \mid + \mid e^{\sin \pi} - e ^{\sin \frac{\pi}{2}} \mid$

$= e- 1- 1 + e = 2e - 2 = 2(e-1)$

Example:

$v(t) = \ln \frac{t}{2}$ on $[1,\ 4]$

$v(t) = \ln \frac{t}{2} = 0 \implies \ln t - \ln 2 = 0$

$\ln t = \ln 2 \implies t = 2$

$\text{Total Distance} = \mid \int_{0}^{2} \left( \ln \frac{t}{2} \right) dt \mid + \mid \int_{2}^{4} \ln \left( \frac{t}{2} \right) dt \mid$

$= \mid \left( t \ln t - t \ln 2\right) _{0}^{2} \mid + \mid \left( t \ln t - t - t \ln 2 \right) _{2}^{4} \mid$

$= \mid (-2 - 2) - (-1 - \ln 2) \mid + \mid (-4) - (-2) \mid$

$= \mid -2 + 1 + \ln 2 \mid + \mid -2 - 4 \ln 2 \mid$

$= \mid \ln 2 - 1 \mid + \mid 4 \ln 2 - 2 \mid = 1 - \ln 2 + 4 \ln 2 - 2$

$= \ln 8 - 1 \approx 1.08$

$\text{Displacement} = \int_{1}^{4} v(t) dt$

Parametrization

Distance is Space

The notion of vector-valued function.

Recall that $\int x dt = xt + C$ and $\int \left( ax^{2}+bx+c da \right) = \frac{a^2}{2}x^2 + (bx+c)a + C$

Two vectors are the same if their magnitude and direction are the same.

Assume we have a function $\vec{p}(t) = (x(t),\ y(t))$ or $\vec{p}(t) = (x(t),\ y(t),\ z(t))$

Then functions $x(t)$ and $y(t)$, and $z(t)$ are components of vector $\vec{p}(t)$. A function $\vec{p}(t)$ continuous and is differentiable if each each component is continuous and differentiable. In that case, $\vec{p}^{\prime}(t) = (x^{\prime}(t),\ y^{\prime}(t),\ z^{\prime}(t))$.

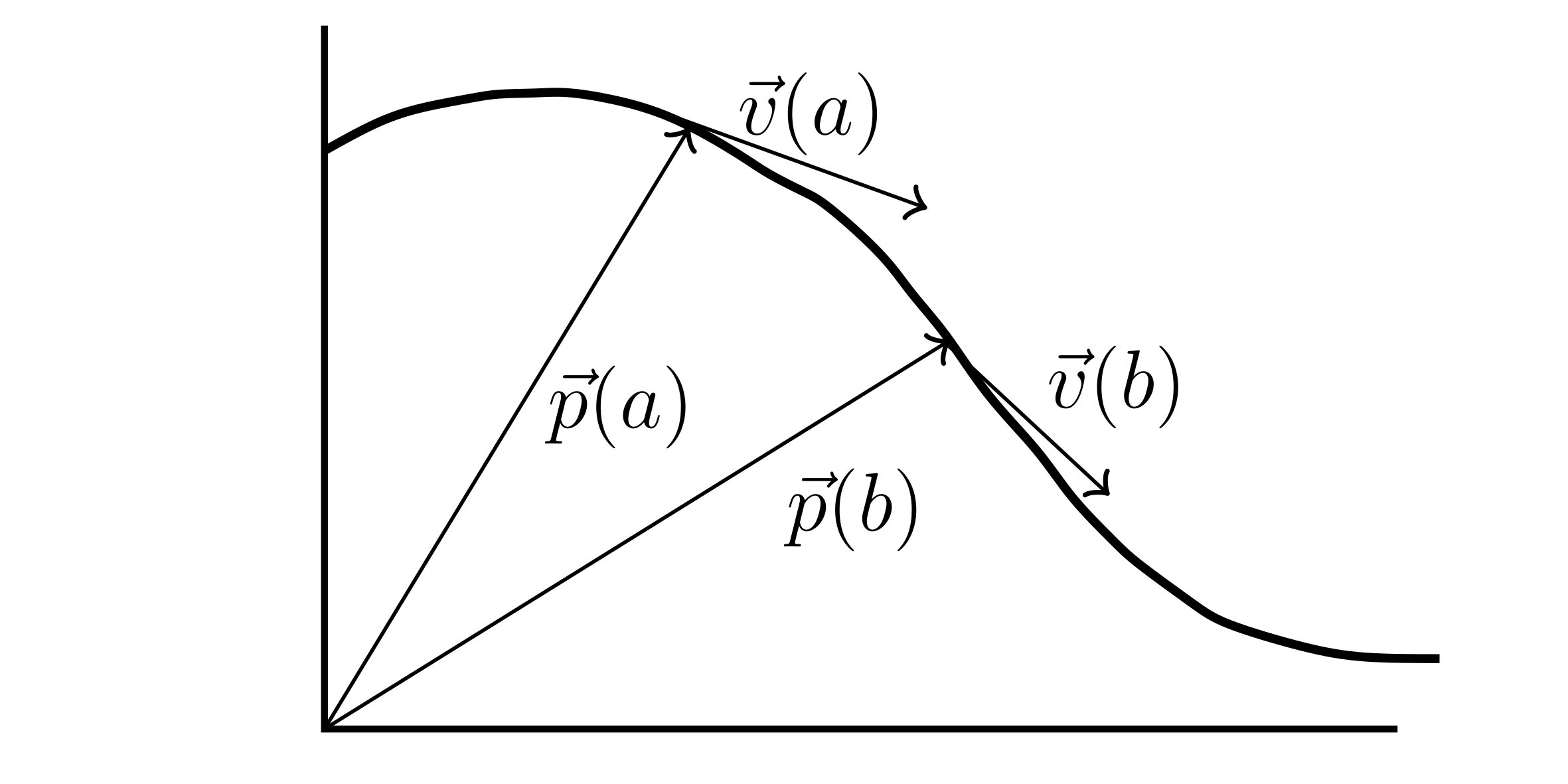
Suppose the position or position vector of the object is given at time $t$.

As: $\vec{p}(t) = (x(t),\ y(t))$

Then, the velocity, which is always tangent to the curve alone which the object is moving, will be:

$\vec{v}(t) = \vec{p}^{\prime}(t) = (x^{\prime}(t),\ y^{\prime}(t))$

If $\vec{v}(t)$ of the object is continuous on the interval $[a,\ b]$, then the displacement of the object between the times $t=a$ and $t=b$ is given by:

$\vec{p}(b) - \vec{p}(a) = \int_{a}^{b} \vec{v}(t) dt$

$\frac{d\vec{p}(t)}{dt} = \vec{v}(t) \implies \int d \vec{p}(t)$

$\vec{p}(b) - \vec{p}(a) = \vec{p}(t) \mid {a}^{b} = \int{a}^{b} \vec{v}(t) dt$

Example:

A particle velocity is given by $\vec{v}(t) = \left( e^{t},\ \sqrt{2},\ -e^{-t} \right) \frac{m}{s}$. What is the displacement of the particle between $t=0$ and $t=1$ second?

$\vec{p}(1) - \vec{p}(0) = \text{Displacement} = \int_{0}^{1} \vec{v}(t)dt$

$\int_{0}^{1} \left( e^{t},\ \sqrt{2},\ -e^{-t} \right) dt = \left( e^{t},\ \sqrt{2}t,\ e^{-t} \right) \mid _{0}^{1}$

$= (e,\ \sqrt{2},\ e^{-1}) - (1,\ 0,\ 1) = (e-1,\ \sqrt{2},\ e^{-1}-1)m$

The magnitude of the displacement.

Therefore, the magnitude of the displacement is $\mid \text{Displacement vector} \mid = \mid (e-1,\ \sqrt{2},\ e^{-1}-1) \mid = \sqrt{(e-1)^{2}+(\sqrt{2})^{2} + \left( e^{-1}-1 \right)^2 }$

Distance:

If $\vec{v}(t)$ is continuous on $[a,\ b]$, then the distance traveled by the object by the object between $t=a$ and $t=b$ is given by:

$\text{Distance} = \int_{a}^{b} \mid \vec{v}(t) \mid dt$

Distance from previous example:

$\int_{0}^{1} \mid \vec{v}(t) dt = \int_{1}^{1} \mid \left( e^{t},\ \sqrt{2},\ -e^{-t} \right) \mid dt$

$= \int_{0}^{1} \sqrt{\left( e^{t} \right) ^{2} + (\sqrt{2})^2 + \left( -e^{-t} \right) ^2 } dt$

$= \int_{0}^{1} \sqrt{e^{2t} + 2 + e^{-2t}} dt$

$= \int_{0}^{1} \sqrt{\left( e^{t}+e^{-t} \right) ^{2}} dt$

$= \int_{0}^{1} \left( e^{t}+e^{-t} \right) dt$

$= \left( e^{t} - e^{-t} \right) \mid _{0}^{1} = \left( e-e^{-1} \right) - (1-1) = e-e^{-1} m$

Note: since $e+e^{-1}-3 > 0$, the distance is always greater than the magnitude of the displacement.

Displacement: $\sqrt{\left( e-e^{-1} \right) ^{2} - 2\left( e+e^{-1}-3 \right) }$

Distance: $e-e^{-1}$

Example:

$\vec{v}(t) = (3 \sin(2\pi t),\ 3 \cos(2\pi t),\ 4t)$ on $[0,\ 2]$

Find the displacement.

$\text{Displacement} = \int_{0}^{2} \vec{v}(t) dt = \int_{0}^{2} (3 \sin (2\pi t),\ 3 \cos (2\pi t),\ 4t) dt$

$= \left( \frac{3}{2\pi} (-\cos (2\pi t)),\ \frac{3}{2\pi} \sin (2\pi t),\ 2t^2 \right) \mid _{0}^{2}$

$= \left( -\frac{3}{2\pi},\ 0,\ 8 \right) - \left( -\frac{3}{2\pi},\ 0,\ 0 \right)$

$= (0,\ 0,\ 8)$

Magnitude of displacement:

$\sqrt{0^{2}+0^{2}+8^2 } = 8$

Find the distance:

$\text{Distance} = \int_{0}^{2} \mid \vec{v}(t) \mid dt = \int_{0}^{2} \mid \left( 3\sin(2\pi t),\ 3 \cos (2\pi t),\ 4t \right) dt$

$= \int_{0}^{2} \sqrt{9\sin ^2(2\pi t) + 9 \cos ^2 (2\pi t) + 16 t^2} dt$

$= \int_{0}^{2} \sqrt{9+16t^2} dt$

$= 3 \int_{0}^{2} \sqrt{1+\left( \frac{4t}{3} \right) ^{2}} dt$

Let $z=\frac{4t}{3}$

$dz = \frac{4}{3}dt \implies dt = \frac{3}{4}dz$

$= \frac{3}{4} \int \sqrt{1+z^{2}} dz$

$= \frac{3}{4} (z \frac{\sqrt{z^{2}+1} }{2} + \frac{1}{2} \ln (z+\sqrt{z^2+1}))$

$= \frac{3}{8} \left( z \sqrt{z^{2}+1} + \ln(z+\sqrt{z^2+1} \right)$

$= \frac{9}{8} \left( \frac{4t}{3}\sqrt{\frac{16t^2}{9}+1} + \ln \left( \frac{4t}{3}+ \sqrt{\frac{16t^2}{9}+1} \right) \right) \mid _{0}^{2} \approx 10.46$

Example:

$\vec{p}(t) = \left( \sin (3t),\ \cos (3t),\ 2t ^{\frac{3}{2}} \right)$ on $[0,\ \pi]$

Displacement: $\vec{p}(\pi) - \vec{p}(0)$

Distance: $\int_{0}^{\pi} \mid \vec{v}(t) \mid dt$

$\vec{v}(t) = \vec{p}^{\prime}(t) = \left( 3 \cos (3t),\ -3 \sin 3t,\ 3t ^{\frac{1}{2}} \right)$

$= \int_{0}^{\pi} \mid \left( 3 \cos (3t),\ -3 \sin(3t),\ 3 t ^{(\frac{1}{2})} \right) dt$

$= \int_{0}^{\pi} \sqrt{9\cos ^{2}(3t) + 9 \sin ^{2} (3t) + 9t} dt$

$= \int_{0}^{\pi} \sqrt{9+9t} dt$

$= 3 \int_{0}^{\pi} \sqrt{1+t}dt$

$= 3 \frac{(1+t)^{\frac{3}{2}}}{\left( \frac{3}{2} \right) } \mid _{0}^{\pi} = 2 (1+t) ^{\left( \frac{3}{2} \right) } \mid _{0}^{\pi}$

$= 2 \left( \left( 1+\pi \right) ^{\left( \frac{3}{2} \right) }- 1 \right)$

Example:

$\vec{v}(t) = (3+4t,\ 5-7t,\ 11t)$ on the interval $[-3,\ 7]$

Displacement: $\int_{-3}^{7} \vec{v}(t) dt$

Distance: $\int_{-3}^{7} \mid (3+4t,\ 5-7t,\ 11t) \mid dt$

$= \int_{-3}^{7} \sqrt{(3+4t)^{2}+(5-7t)^2+ 2t ^{2}}dt$

Example:

$\vec{p}(t) = (-t,\ t,\ 3)$ on interval $[0,\ \frac{\pi}{4}]$

---

Next Monday is the last quiz before the midterm.

• Midterm: 10:00-11:30

---

Arc Length

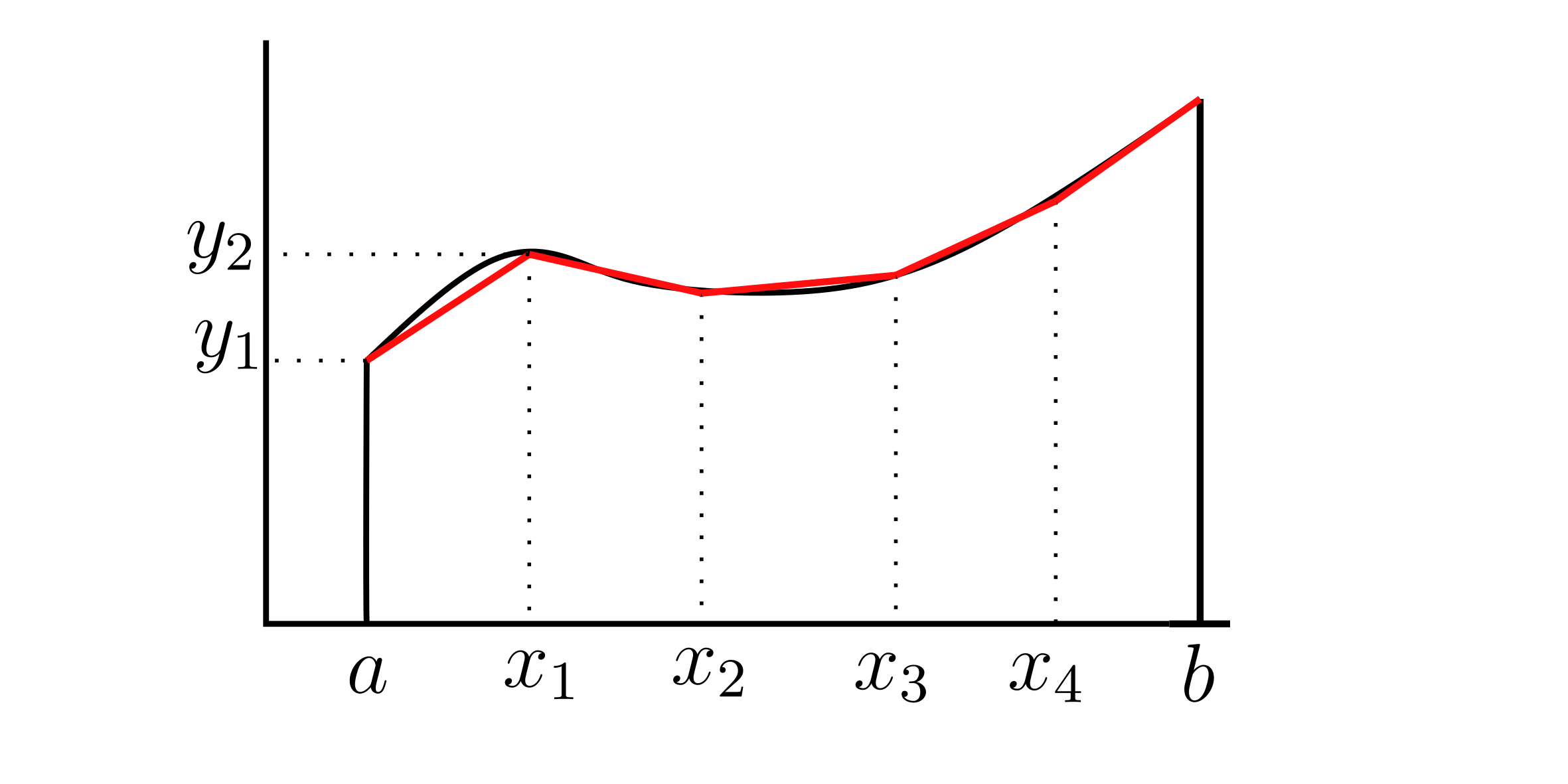
Inscribed polygon in the graph above

We define the length L of the curve C given by equation $y=f(x)$ on $a\le x\le b$ as the limit of the inscribed polygon (if the limit exists).

$L = \lim_{n \to \infty} \sum_{i=1}^{n} \mid P_{i-1},\ P_i \mid$ (The difference of the two points)

$\Delta x$ is always the same. If we let $\Delta y_i = y_i - y_{i-1}$ then $\mid P_{i-1},\ P_i \mid = \sqrt{\Delta x^{2} + \Delta y_i ^{2}} = \sqrt{\left( x_i - x_{i-1} \right) ^{2} + \left( y_i - y_{i-1} \right) ^{2}}$.

$\Delta y_i = f^{\prime}(x_i^*)$, therefore we have:

$\mid P_{i-i},\ P_i \mid = \sqrt{(\Delta x)^2 + (\Delta x)^2 f ^{\prime}(x_i^\star)^2} = \sqrt{1 +f^{\prime}(x_i^*)^2} \Delta x$

Then $L = \lim_{n \to \infty} \sum_{i=1}^{n} \mid P_{i-1},\ P_i \mid$

$= \lim_{n \to \infty} \sum_{i=1}^{n} \sqrt{1+f^{\prime}(x_i^*)^2} \Delta x = \int_{a}^{b} \sqrt{1+\left( f^{\prime}(x) \right) ^{2}} dx$

Riemann Sum:

$\int_{a}^{b} f(x) dx = \lim_{n \to \infty} \sum_{i=1}^{n} f(x_i) \Delta x$ Say that $\sin ^2 x = 1 + \left( y^{\prime} \right) ^{2}$

$y^{\prime} = \sin ^2 x - 1$

$y = \int \left( \sin ^2 - 1 \right) dx$

Example:

Find the arc length of the curve $y = x^2 - \frac{\ln (x)}{8}$ for $1\le x\le 2$

$L = \int_{1}^{3} \sqrt{1+ (y^{\prime})^2} dx$

$y^{\prime} = 2x - \frac{1}{8x} \implies \left( y^{\prime} \right)^{2} = \left( 2x - \frac{1}{8x} \right)^{2} = 4x^{2}-\frac{1}{2}+\frac{1}{64x^2}$

$\left( 2x + \frac{1}{8x} \right) ^{2} = 1 + 4x^2 - \frac{1}{2} + \frac{1}{64x^2} = 4x^2 + \frac{1}{2} + \frac{1}{64x^2}$

$= \int_{1}^{3} \sqrt{\left( 2x+\frac{1}{8x} \right) ^{2}} dx = \int_{1}^{3} \left( 2x+\frac{1}{8x} \right) dx$

$= \left( x^{2} + \frac{1}{8}\ln x \right) \mid _{1}^{3} = 8 + \frac{\ln 3}{8} \approx 8.1373$

Example:

Find L if $x(y) = \frac{e^y + e^{-y}}{2} = \cosh (y)$ for $0\le y\le \ln 3$ $L = \int_{0}^{\ln 3} \sqrt{1+ \left( x’^2 \right) } dy$

$x^{\prime} = \frac{e^2-e^{-y}}{2} \implies (x’)^2 = \left( \frac{e^y-e^{-y}}{2} \right) ^{2}$

$1+(x’)^2 = 1 + \frac{e^{2y}-2+e^{-2y}}{4}$

$= \frac{e^{2y}+2+e^{-2y}}{4} = \left( \frac{e^{y}+e^{-y}}{2} \right) ^{2}$

$L = \int_{0}^{\ln 3} \sqrt{\left( \frac{e^y+e^{-y}}{2} \right) ^{2}} dy = \frac{4}{3}$

Example:

Length of arc defined by $f(x)= \frac{x^3}{12}+\frac{1}{x}$ on the interval $[1,\ 2]$. This equals $\frac{13}{12}$

Example:

Length of arc defined by $g(x)=\ln (\sin x)$ on the interval $[\frac{\pi}{4},\ \frac{\pi}{2}]$.

$L = \int_{\frac{\pi}{4}}^{\frac{\pi}{2}} \sqrt{1 + \left( \left( \ln (\sin x) \right) ‘ \right) ^{2}}$

$\left( \ln \sin x \right)’ = \frac{\cos x}{\sin x} = \cot x$

$(\ln \sin x)’ ^{2} = \cot ^2 x$

$1+\cot ^2 x = \csc ^2 x$

$L = \int_{\frac{\pi}{4}}^{\frac{\pi}{2}} \csc x dx$

$= \int \frac{dx}{\sin x} = \int \frac{\sin x}{\sin ^2 x} dx = \int \frac{\sin x}{1- \cos x} dx$

$z = \cos x$

$dz = - \sin x dx$

$= - \int \frac{dz}{1-z^2} = - \int \frac{dx}{(1-z)(1+z)}$

$= \ln (\csc x - \cot x)$

Example: $\int_{1}^{3} x^{3} dx$

$\Delta x = \frac{b-a}{n}$

Left-hand side:

$x_i = 1+\frac{2i}{n}$

Volumes of Revolution

Postulates:

• Never awkward shapes – only volumes of revolution
• If you can invert the function, the problem can be solved by either method (it’s just preference/ease)
• Axis of integration has nothing to do with shell/disk

Do the following integral by using $\int_{1}^{3} … dy$ : $y=x^2+1$

Disk Method

Consider a pile of CD disks.

$V= \lim_{n \to \infty} \sum_{i=1}^{n} A_i(x) dx = \int_{a}^{b} A(x) dx$

Example:

Find the volume of the shape obtained by rotating $y=\sqrt{x}$ across the x axis from from $x=0$ to $x=1$.

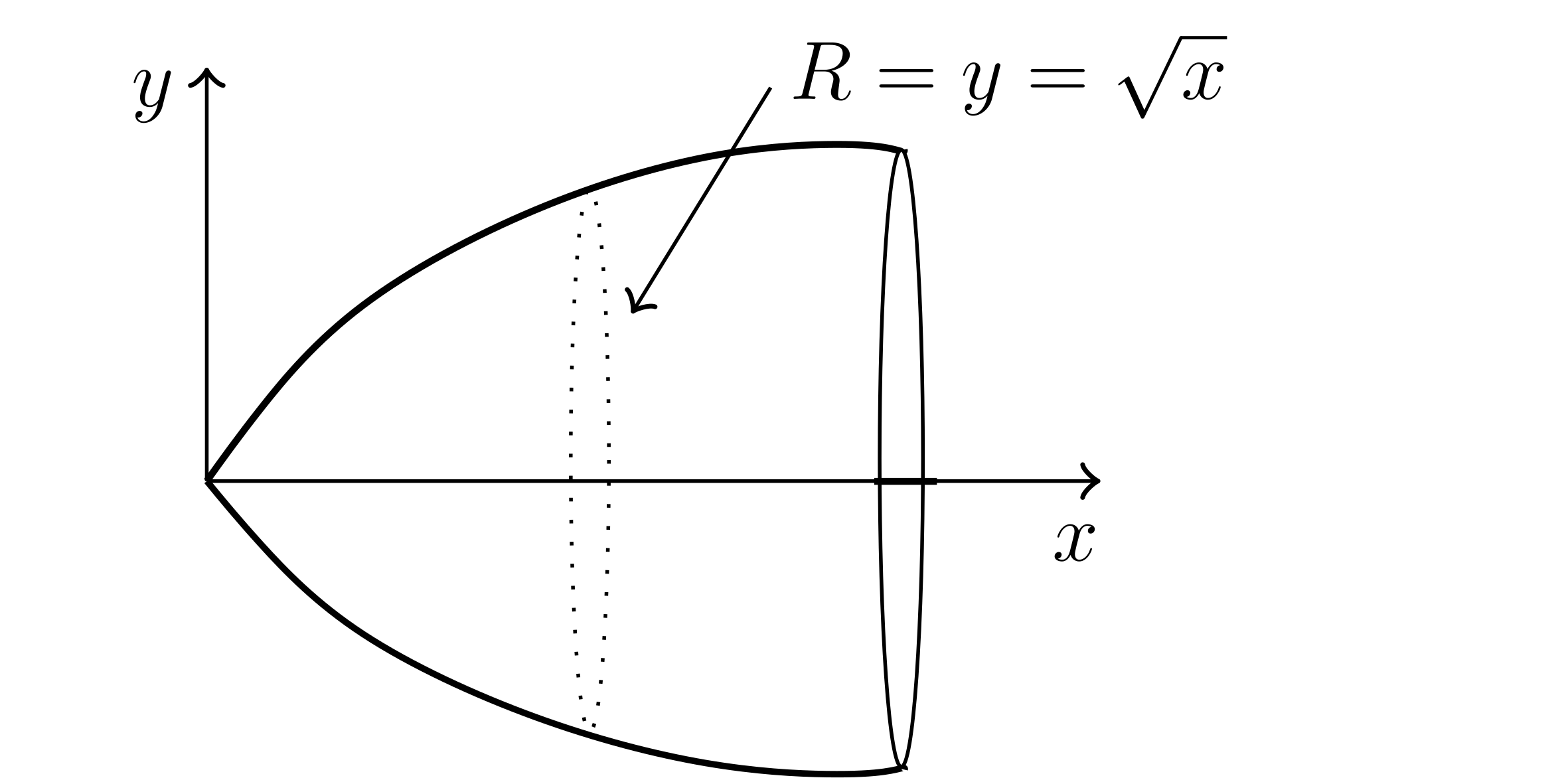
$V^{\text{Disk}} = \int_{0}^{1} A(x) dx$

$A(x) = \pi R^{2}$

$A(x) = \pi \left( \sqrt{x} \right) ^{2} = \pi x$

$V = \int_{0}^{1} \pi x dx = \pi \frac{x^2}{2} \mid _{0}^{1} = \frac{\pi}{2}$

Example

Find $v$, rotating $y=x^2$, $y=8$, $x=0$ above the y-axis.

$A(y) = \pi R^{2} = \pi x^2$

$x = ^{3} \sqrt{y} = y^{\frac{1}{3}}$

$V = \int_{0}^{8} A(y) dy = \pi \int_{0}^{8} y^{\frac{2}{3}}dy$

$= \pi \frac{y^{\frac{5}{3}}}{\frac{5}{3}} \mid _{0}^{8}$

$= 96 \frac{\pi}{5}$

Washer

Example:

$y=x,\ y=x^2$ about x-axis.

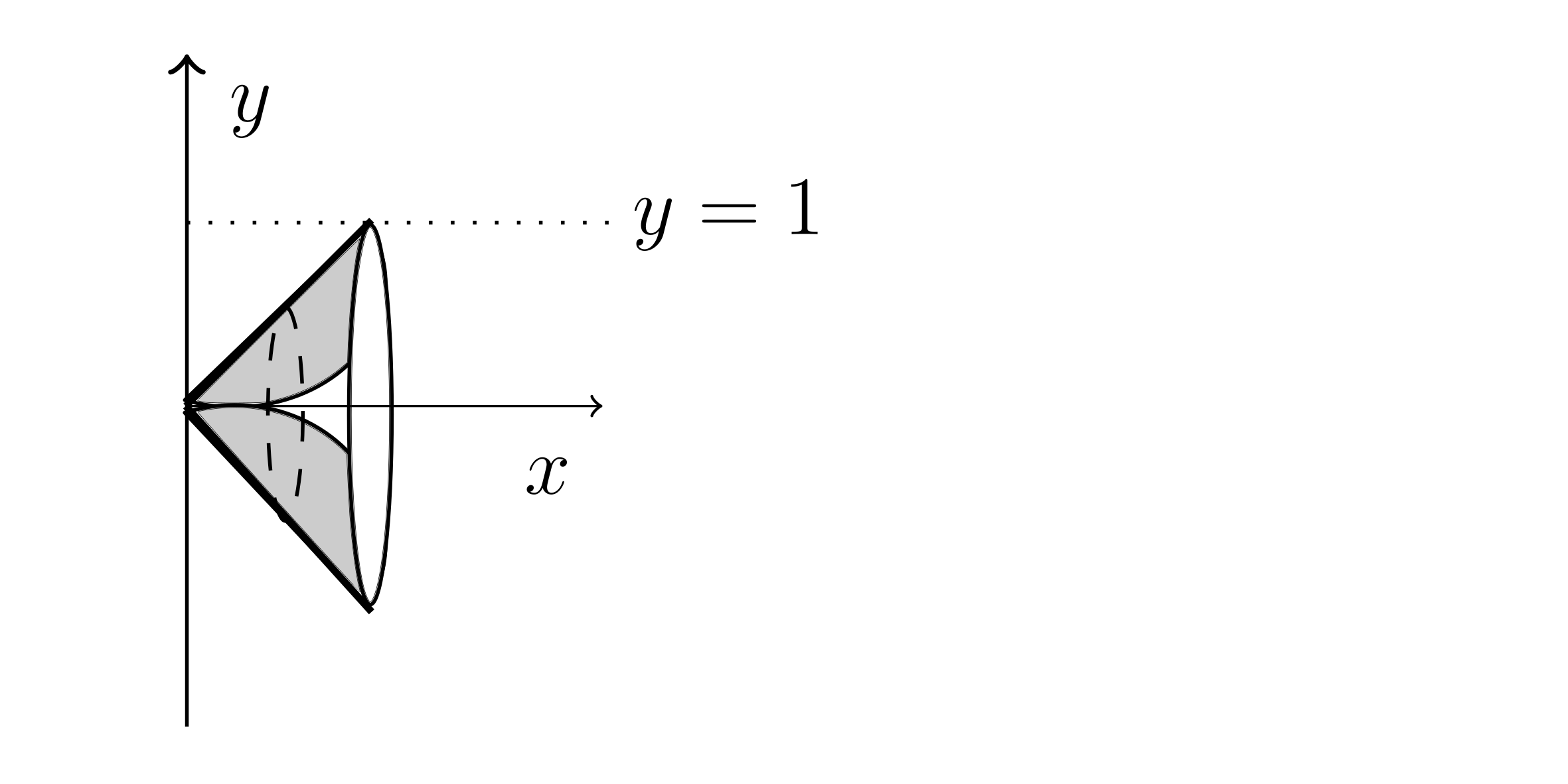
$y_1 = y_2 \implies x=x^2 \implies x_0 = 0,\ x=1$

$V^{\text{Disk}} = V^{\text{Washer}} = \int_{0}^{1} A(x) dx$

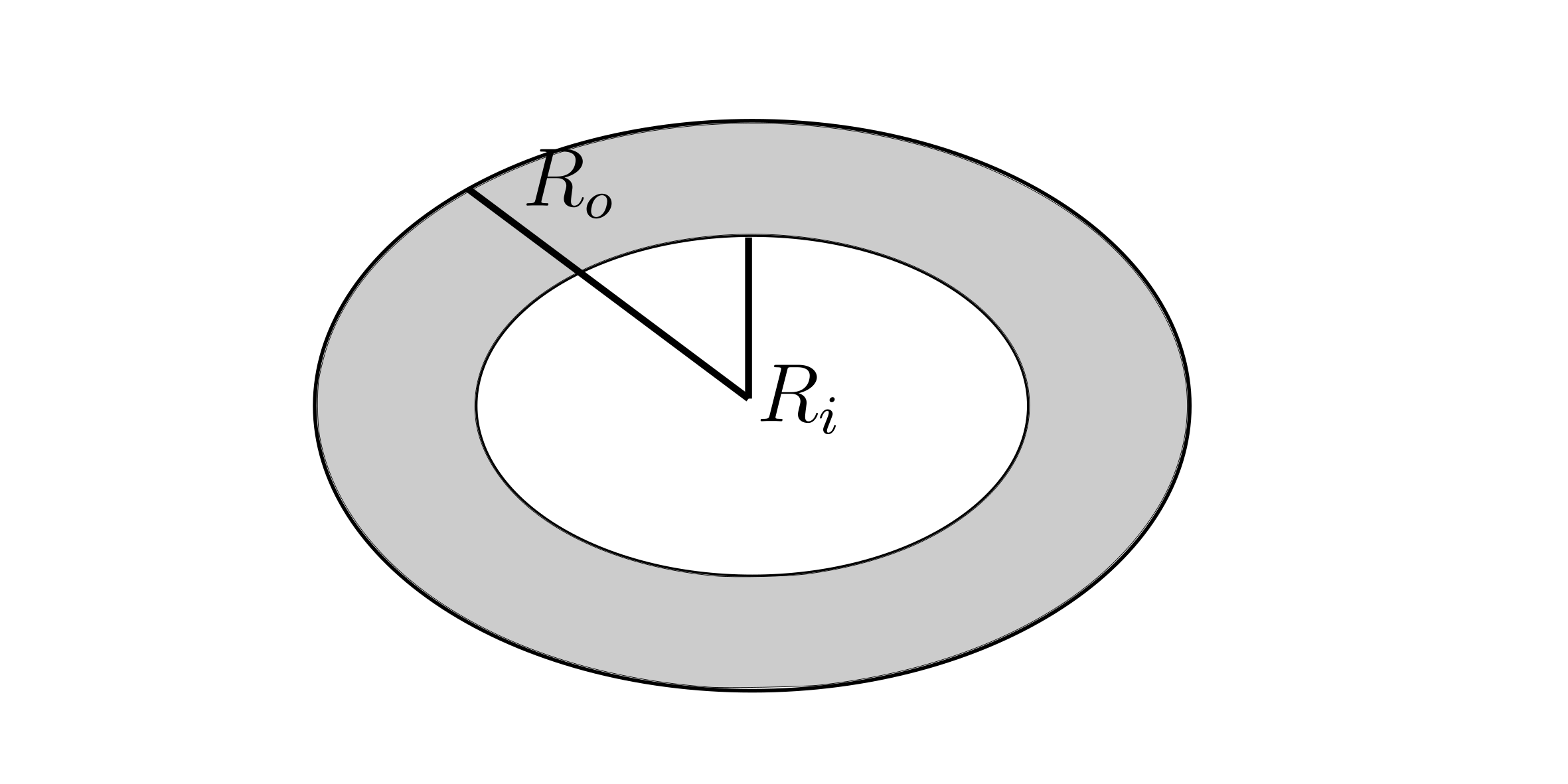
$R_o = y_1 = x$

$R_i = y_2 = x^2$

$A(x) = \pi R _o^2 - \pi R _i^2 = \pi \left( R _o^2 - r _i^2 \right)$

$= \pi \left( x^2 - x^4 \right)$

$V = \int_{0}^{1} \left( x^2 - x^4 \right) dx = \pi \left( \frac{x^3}{3} - \frac{x^5}{5} \right) \mid _{0}^{1}$

$= \pi \left( \left( \frac{1}{3} - \frac{1}{5} \right) -0 \right) = \frac{2\pi}{15}$

Example:

$y=x,\ y=x^2$ rotated around $y=2$

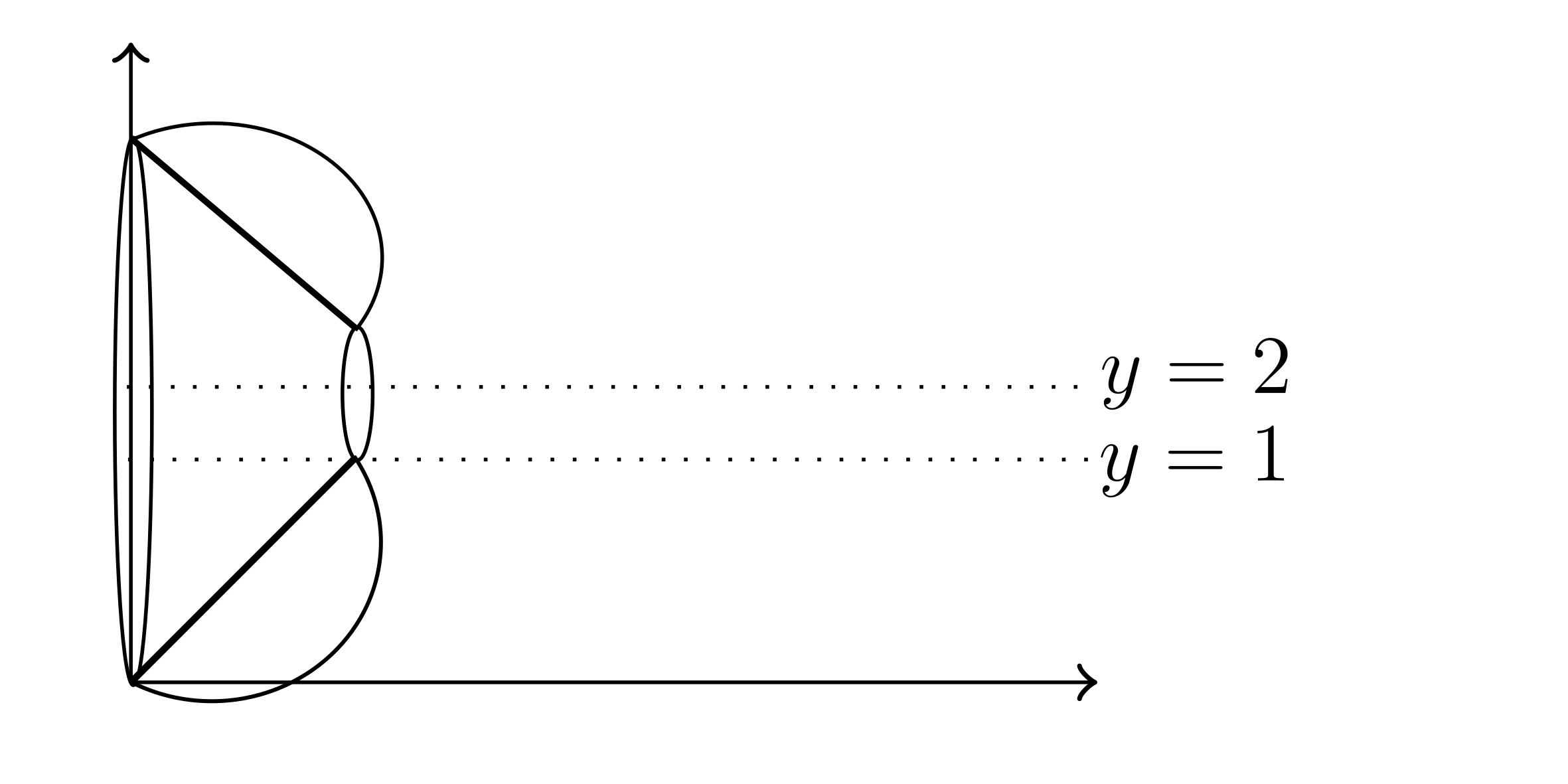
$V^{\text{Washer}} = \int_{0}^{1} A(x) dx$

$A(x) \pi \left( R _o^2 - r _i^2 \right)$

$R_o = 2- y_1 = 2- x^2$

$R_i = 2-y_2 = 2 - x$

$V^{\text{Disk}} = \pi \int_{0}^{1} \left( 2-x^2 \right)^2 - \left( 2-x \right)^2 dx = \frac{8\pi}{15}$

Example (same one, but rotated differently):

$y=x,\ y=x^2$ rotated around $x=-1$

$V^{\text{Disk}} = \int_{0}^{1} A(y) dy$

$R_o = x_1 - (-1) = \sqrt{y} +1$

$R_i = x_2 - (-1)= y +1$

$\pi \int_{0}^{1} \left( \sqrt{y} +1 \right) ^{2} - \left( y+1 \right) ^{2} dy = \frac{\pi}{2}$

Example (same, rotated differently):

$y=x,\ y=x^2$ rotating around $x=3$

$V^{\text{Disk}} = \int_{0}^{1} A(y) dy$

$R_o = \text{axis} - \text{var} = 3 - x_1 = 3-y$

$R_i = \text{axis} - \text{var} = 3 - x_2 = 3-\sqrt{y}$

Shell Method

Different methods of volumes of revolution.

$V_i = A(x_i) h = A(x_i) f(x)$

$V_i - 2\pi x_i \Delta x f(x_i)$

$V = \lim_{n \to \infty} \sum_{i=1}^{n} 2\pi x_i \Delta x f(x_i)$

$\int_{a}^{b} 2\pi x f(x) dx = \int_{a}^{b} 2\pi R h dx$

Example:

$V^{\text{Shell}} = \int_{a}^{b} 2\pi R h dx$

$V^{\text{Shell}} = \int_{a}^{b} 2\pi f(x) dx$

Or, if we are going around the y axis:

$V^{\text{Shell}} = \int_{a}^{b} 2 \pi R h dy$

Example:

Find the volume obtained by rotating about y-axis, the region bounded by $y=2x^2 - x^3$ and $y=0$ (the x-axis). Note, you cannot get the inverse of that function

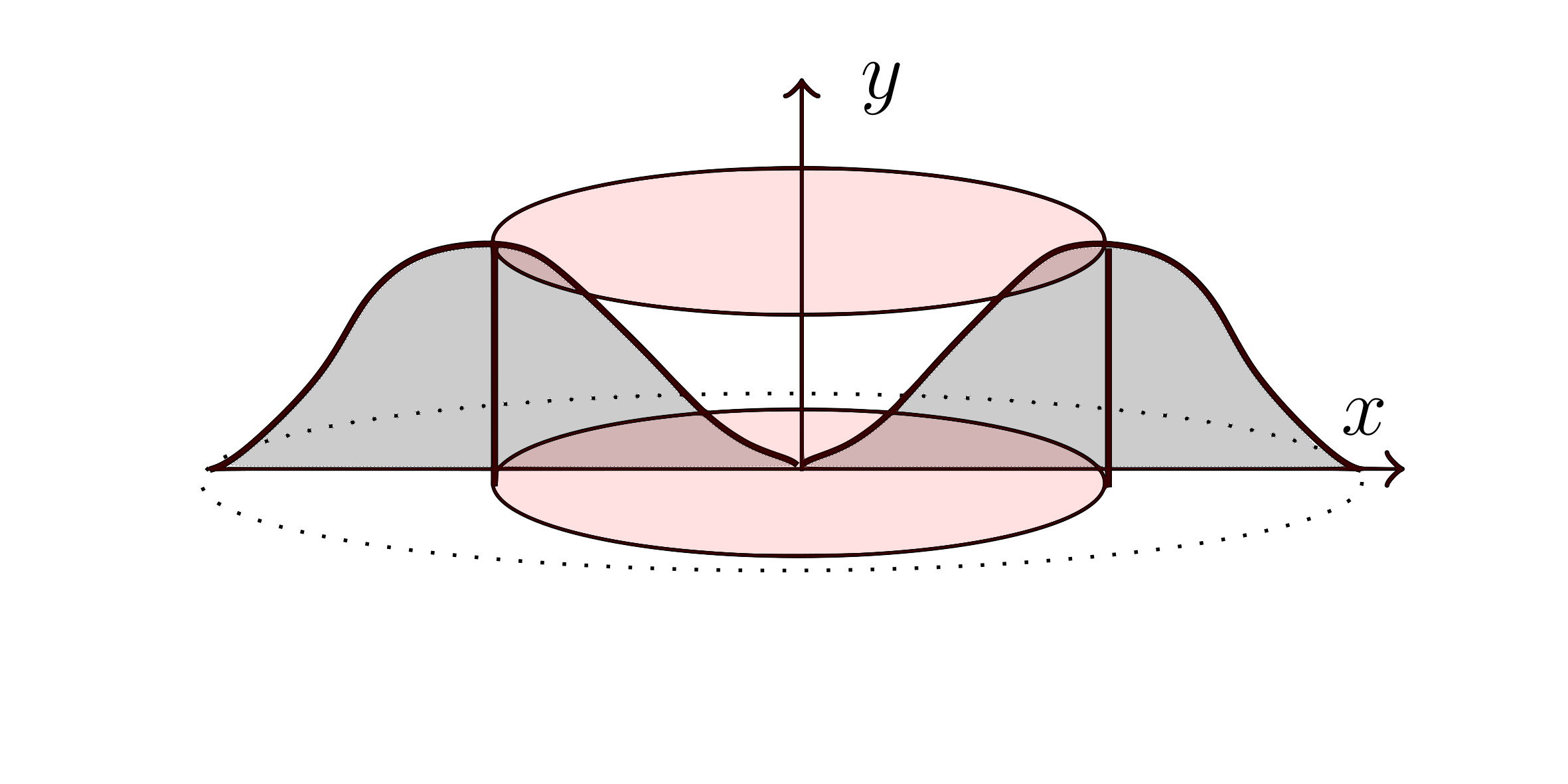
The red is the elemental shell.

$y =0 = 2x^2 - x^3$

$x^2 (2-x) = 0$

$\therefore x = 0,\ x=2$

$V^{\text{Shell}} = \int_{0}^{2} 2\pi R h = dx$

$h = y = 2x^2 - x^3$

$V^{\text{Shell}} = \int_{0}^{2} 2\pi x\left( 2x^2 - x^3 \right) dx = \frac{16\pi}{5}$

Can we do this using the disk method?

• It’s a lot harder because you need to get a $R_i$ and $R_o$.

You can use disk method with this, however, it is overly complicated.

Example:

$y=x$ and $y=x^2$ about y-axis

$V^{\text{Shell}} = \int_{0}^{1} 2 \pi R h dx$

$h(x) = y^{\text{top}} - y^{\text{bottom}}$

$V^{\text{Shell}} = \int_{0}^{1} 2 \pi x (x-x^2) dx$

$= 2\pi \int_{0}^{1} (x^2 - x^3) dx = 2\pi \left( \frac{x^3}{3}-\frac{x^4}{4} \right) \mid _{0}^{1}$

Now let’s use disk method:

$V^{\text{Disk}} = \int_{0}^{1} A(y) dy$

$A(y) = \pi \left( R _{o}^2 - R _{i}^2 \right)$

$R_o = \sqrt{y}$

$R_i = y$

$= \int_{0}^{1} \pi \left( y-y^2 \right) dy$

$= \frac{\pi}{6}$

Example:

$y=x$ and $y=x^2$ about the x-axis

Disk method:

$V^{\text{Disk}} = \int_{0}^{1} A(x) dx$

$A(x) = \pi \left( R _o^{2} - R _i^2 \right)$

$V^{\text{Disk}} = \int_{0}^{1} \pi \left( x^2 - x^4 \right)$

$= \pi \left( \frac{x^3}{3}- \frac{x^5}{5} \right) \mid _{0}^{1} = \frac{2\pi}{15}$

Shell method:

$y=x \implies x^{\text{Left}} = y$

$y=x^2 \implies x^{\text{Right}} = \sqrt{y}$

$V^{\text{Shell}} = \int_{0}^{1} 2 \pi R h dy$

$R = y$

$h(y) = x^{\text{Right}} - x^{\text{Left}} = \sqrt{y} -x$

$V^{\text{Shell}} = \int_{0}^{1} 2 \pi y\left( \sqrt{y} -y \right) dy$

$= 2\pi \int_{0}^{1} \left( y^{\frac{3}{2}} - y^{2} \right) dy$

$= 2\pi \left( \frac{y^{5}2}{\frac{5}{2}} - \frac{y^3}{3} \right) \mid _{0}^{1}$

$= \frac{2\pi}{15}$

Example:

$y=x$ and $y=x^2$ about $y=2$

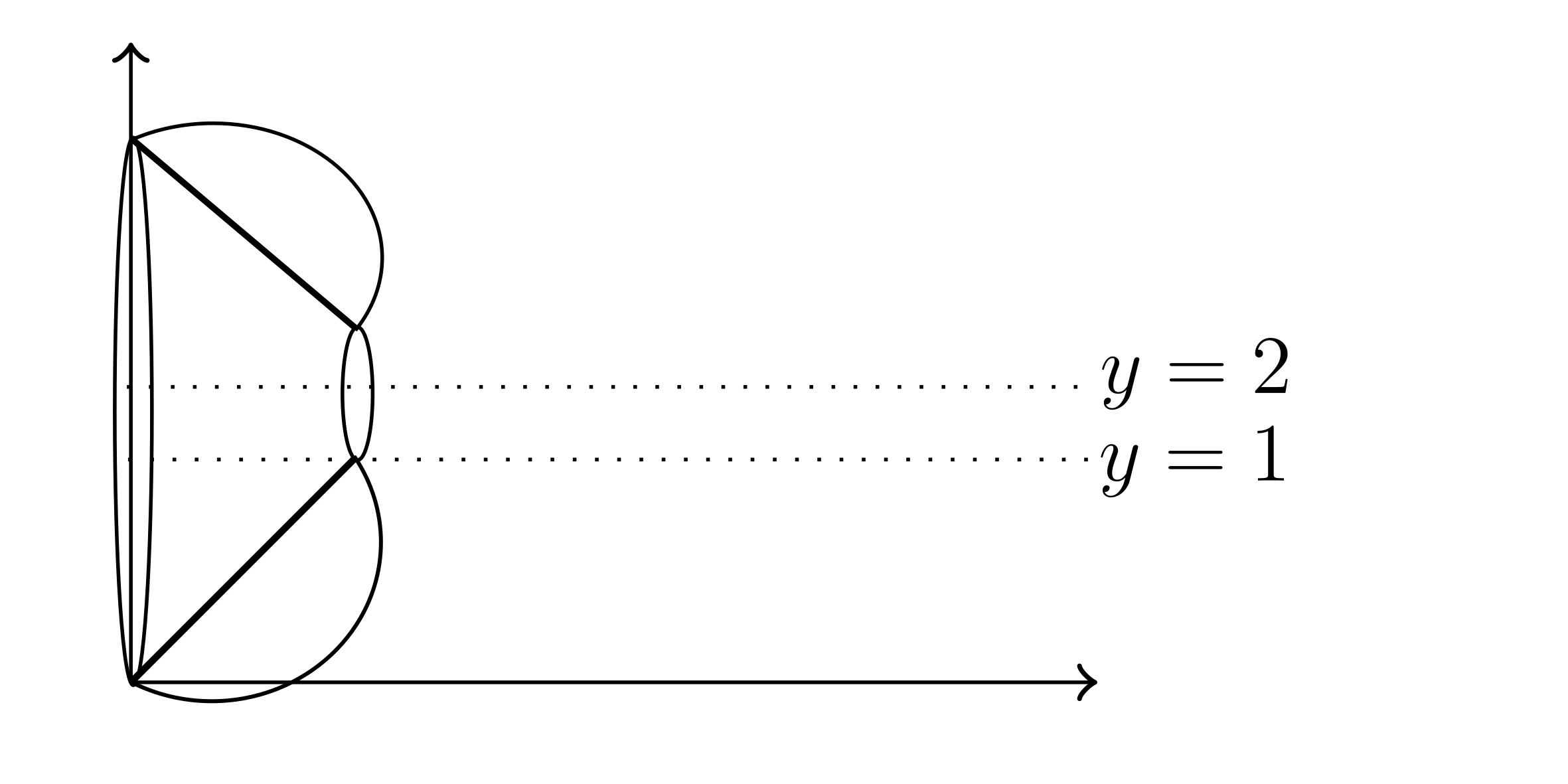
$V^{\text{Shell}} = \int_{0}^{1} 2 \pi R h dy$

$R = \left( 2-y \right)$

$h(y) = \sqrt{y} - y$

$= 2\pi \int_0^1 \left( 2-y \right) \left( \sqrt{y} -y \right) dy$

$= 2\pi \int_{0}^{1} \left( 2\sqrt{y} -2y-y^{\frac{3}{2}}+y^{2} \right) dy$

$= \frac{8\pi}{15}$

Example:

$y = \sin x$ about y-axis on $[0,\ \pi]$

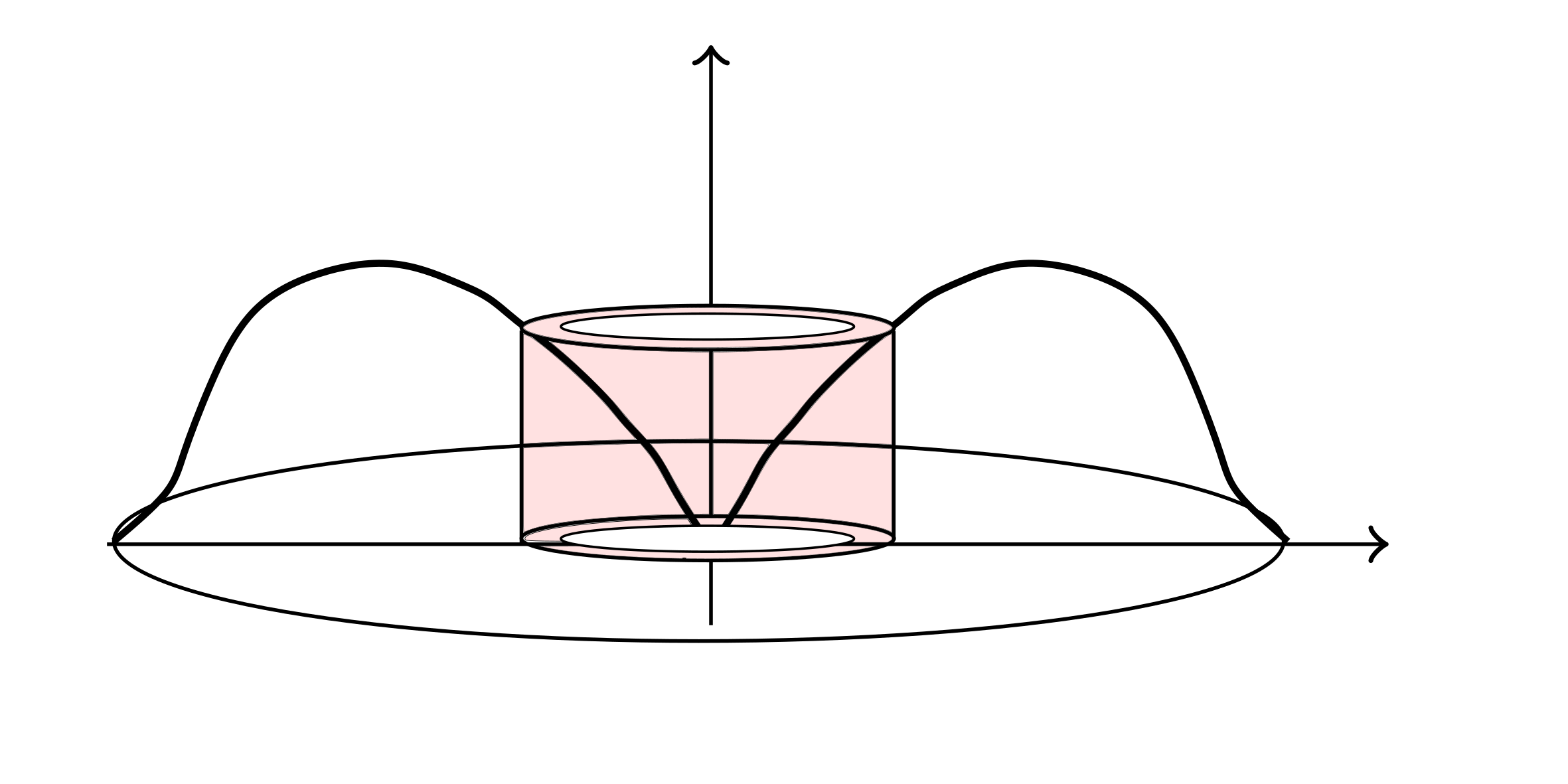
$V^{\text{Shell}} = \int_{0}^{\pi} 2\pi R h dx$

$R = x$

$h= \sin x$

$= 2\pi \int_{0}^{\pi} x \sin x dx = 2\pi^{2}$

Disk method

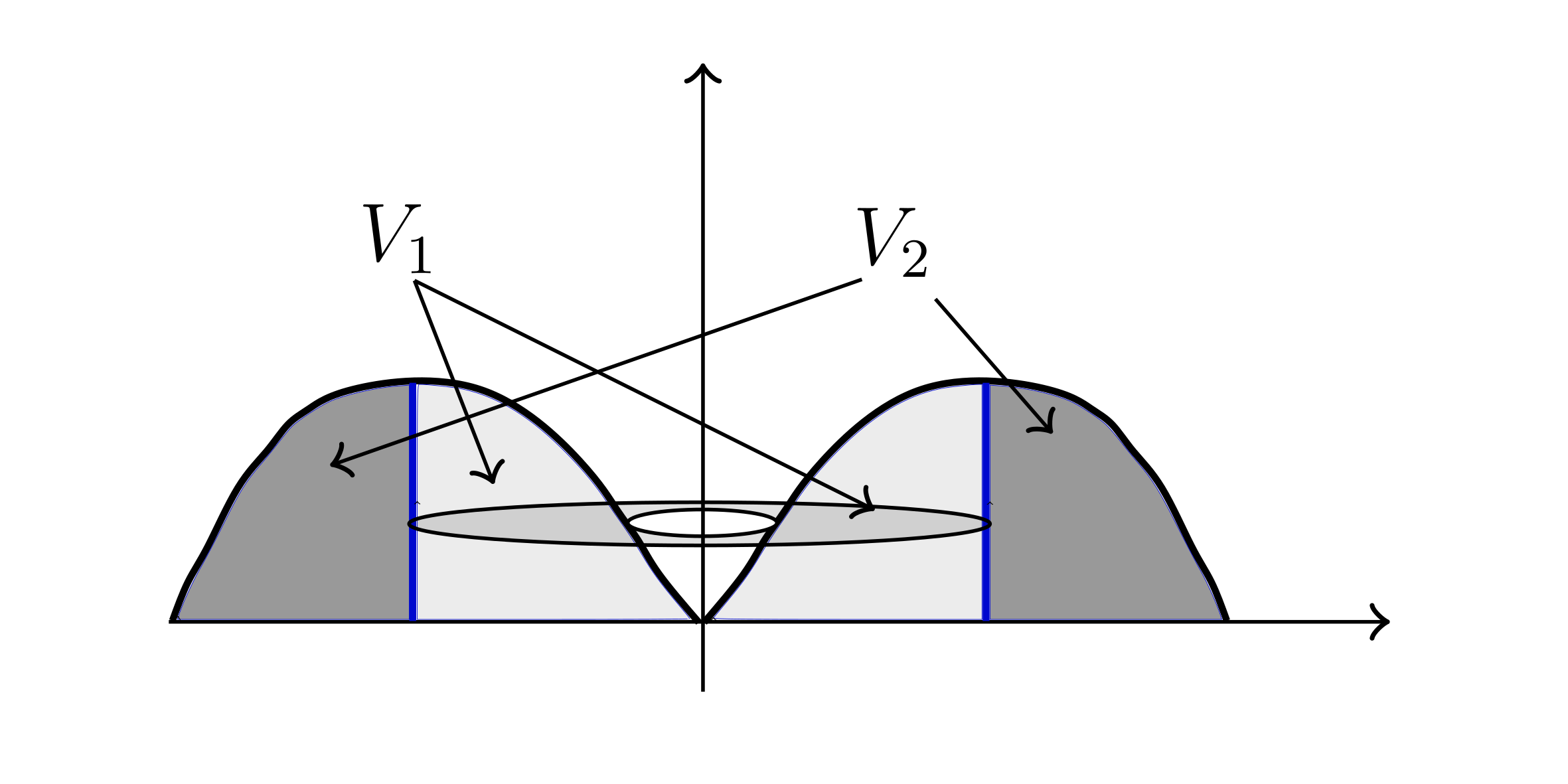
$V^{\text{Disk}} = V_1 + V_2$

$V_1 = \int_{0}^{1} A(y) dy$

$A(y) = \pi \left( R _o^2 - R _i^2 \right)$

$R_o = \frac{\pi}{2}$

$R_i = \sin ^{-1} y$

$A(y) = \pi \left( \left( \frac{\pi}{2} \right) ^{2} - \left( \sin ^{-1} y \right) ^{2} \right)$

$V = \pi \int_{0}^{1} \left( \left( \frac{\pi}{2} \right) ^{2} - \left( \sin ^{-1}y \right) ^2 \right) dy + V_2$

$V_2 = \int_{0}^{1} A(y) dy$

$A(y) = \pi \left( R _o^2 - R _i ^2 \right)$

$= \pi \int_{0}^{1} \left( \left( \pi - \sin ^{-1}y \right) ^{2} - \left( \frac{\pi}{2} \right) ^{2} \right)dy$

$V^{\text{Disk}} = \pi \int_{0}^{1} - \left( \sin ^{-1}y \right) ^{2} + \pi^2 - 2 \pi \sin ^{-1} y + \left( \sin ^{-1} \right) ^{2} dy$

$= \pi \int_{0}^{1} \pi^{2} - 2\pi \sin ^{-1}y dy$

$= \pi \left( \pi ^2 y - 2 \pi y \sin ^{-1} y - 2\pi \sqrt{1-y^2} \right) \mid _{0}^1$

Mass and Density

Area and density. If we have a 2D region on an xy-plane, we will assume that the density is constant in each cross-sectional line segment perpendicular to x- or y-axis. For each fixed x, it is $\delta_{\text{area}}\left( x \right)$.

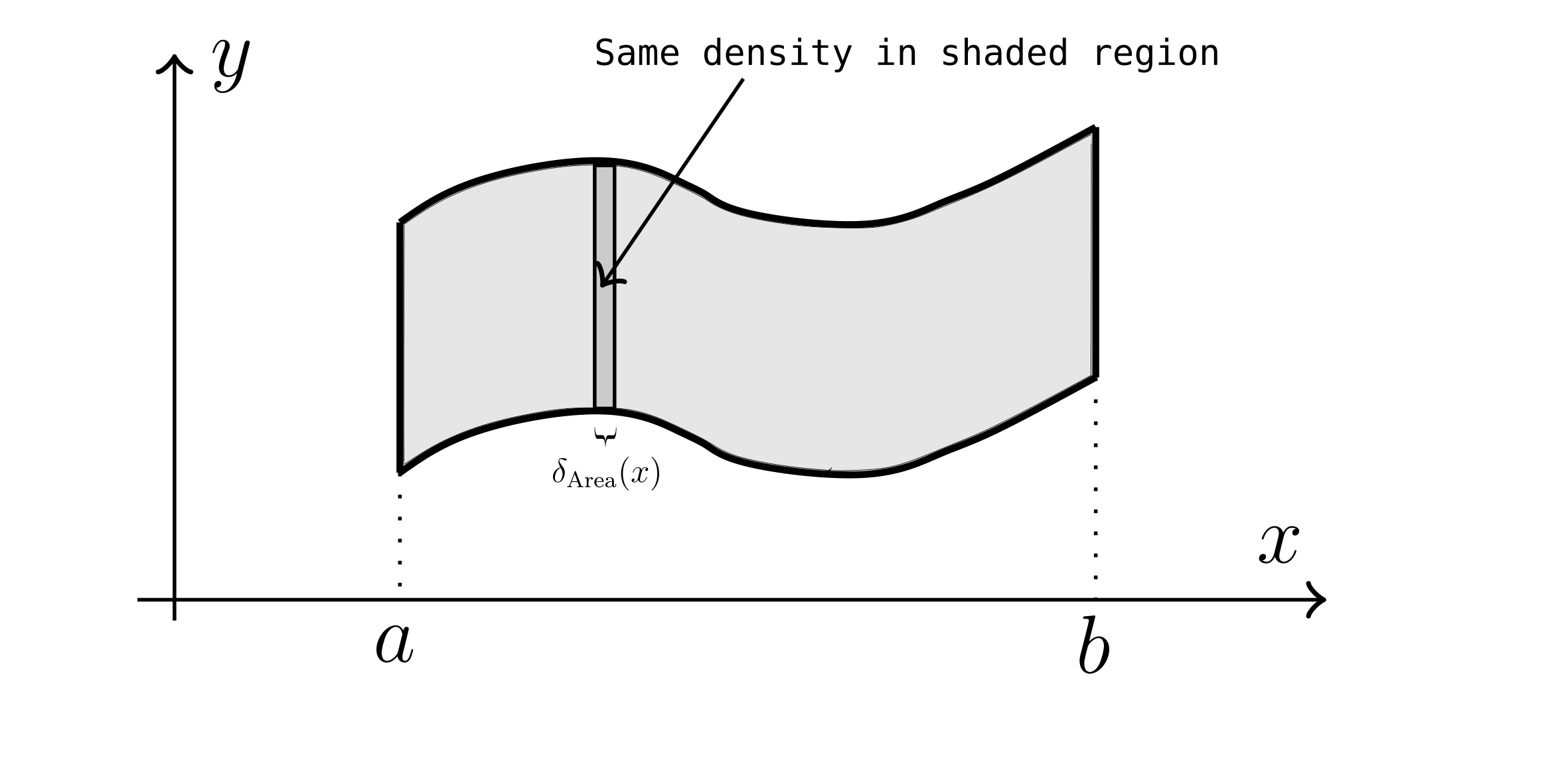
If we know the function $h(x)$, which is the height of the cross-sectional line segment in the region. Then the infinitesimal area of the cross-section (or infinitesimal thin rectangle) is $dA = h(x) dx$ and infinitesimal mass is $\delta = \frac{m}{v}$.

$\delta _{\text{Area}} = \frac{m}{A}$

$d m = \delta _{\text{Area}} (x) dA$

Total mass $M = \int_{a}^{b} dm = \int _{a}^{b} \delta _{\text{Area}}(x) dA = \int _{a}^{b} \delta _{\text{Area}}(x) h(x) dx$.

Example:

A thin plate occupies region in xy-plane below the line $y=2-x$.

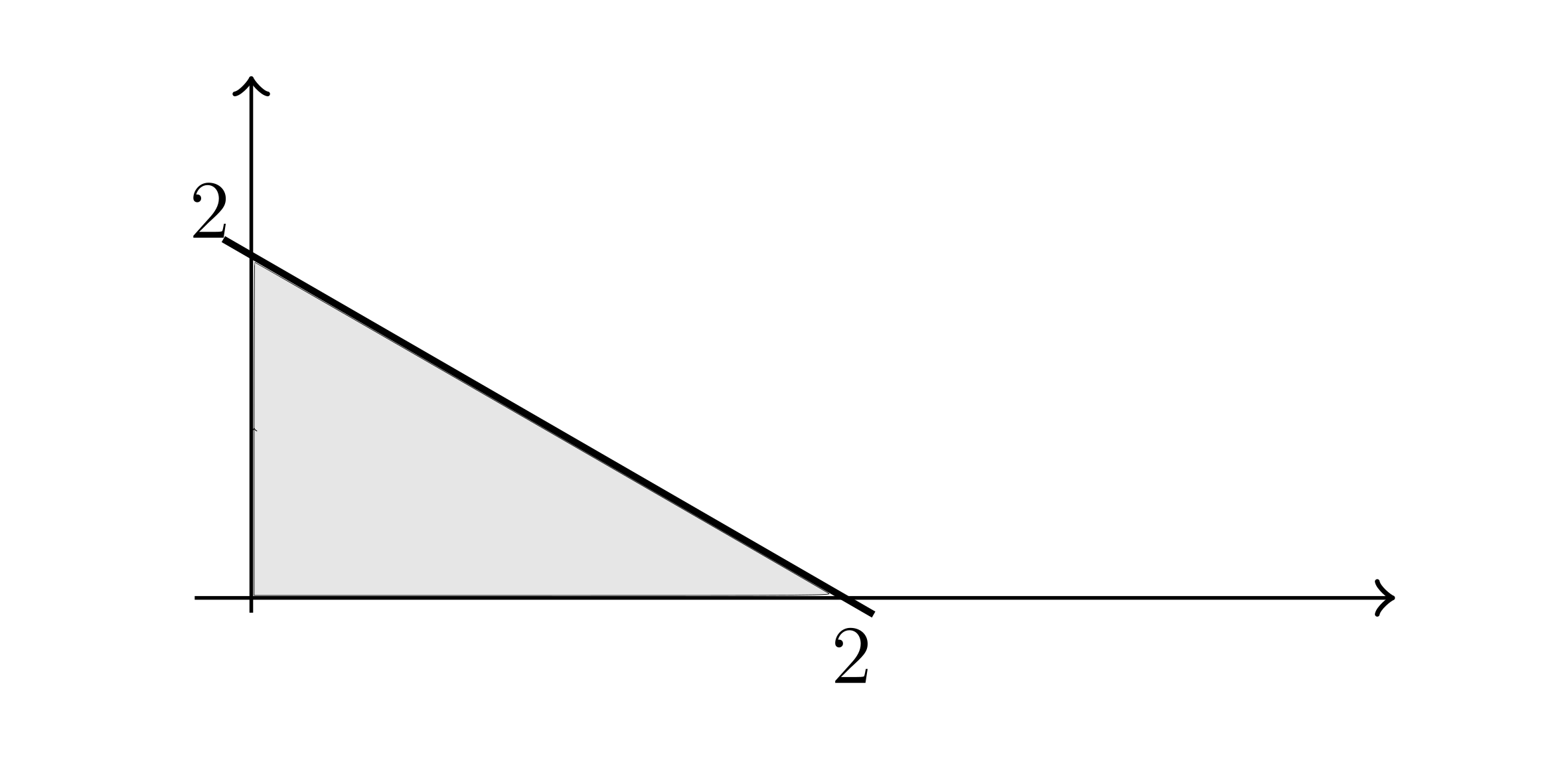
Let the area-density be $\delta _{\text{Area}}(y) = e^{-y} \frac{\text{kg}}{\text{m}^{2}}$

Find m.

$m = \int_{0}^{2} \delta _{\text{Area}} (y) dA = \int _{0}^{2} e^{-y}h(y) dy$

$h(y) = x^R - x^L = \left( 2-y \right) - 0 = 2 - y$

$m = \int_{0}^{2} e^{-y}(2-y) dy$

$m = -2 (e^{-2}-1) - \int_{0}^{2} y e^{-y} dy = e^{-2}+1 \text{kg}$

Example:

• Expect this type of problem on the exam

$y=2x-6$

$\delta _{\text{Area}}(x) = x^2 + 1$

$m = \int_{0}^{3} \delta _{\text{Area}}h(x) dx$

$h(x) = y^T - y^B$

$m= \int_{0}^{3} \left( x^2 + 1 \right) \left( 0 - \left( 2x-6 \right) \right) dx = \frac{45}{2}$

Example:

$\delta _{\text{Area}} (y) = y^{\frac{3}{2}} + 2$

$y= \sqrt{x} \implies x = y^2$

$x=4$

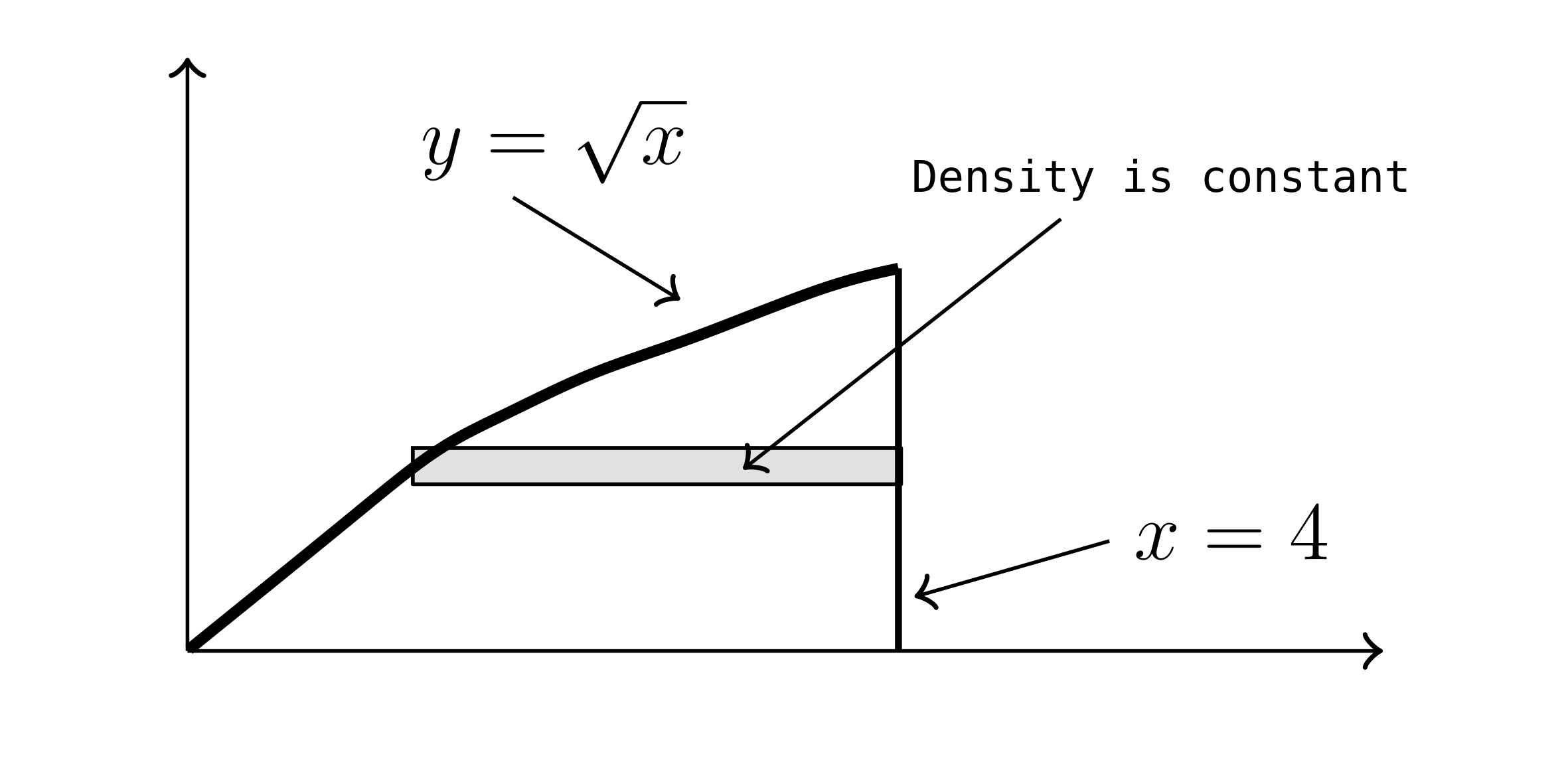
$m = \int_{0}^{2} \delta _{\text{Area}}(y) h(y) dy$

$h(y) = x^R - x^L = 4 - y^2$

$m = \int_{0}^{2} \left( y^{\frac{3}{2}} + 2\right) \left( 4-y^2 \right) dy$

$m \approx 14.689 \text{ kg}$

Example:

$y = \sqrt{x}$

$y = x^2$

$\delta _{\text{Area}} (y) = y^{2} + 1$

$m = \int_{0}^{1} \left( y^{2}+1 \right) \left( \sqrt{y} -y^2 \right) dy$

Moments and Center of Mass

“Give me a lever long enough and a fulcrum on which to place it, and I shall move the world.” - Archimedes

Archimedes experimentally discovered that rod will balance it.

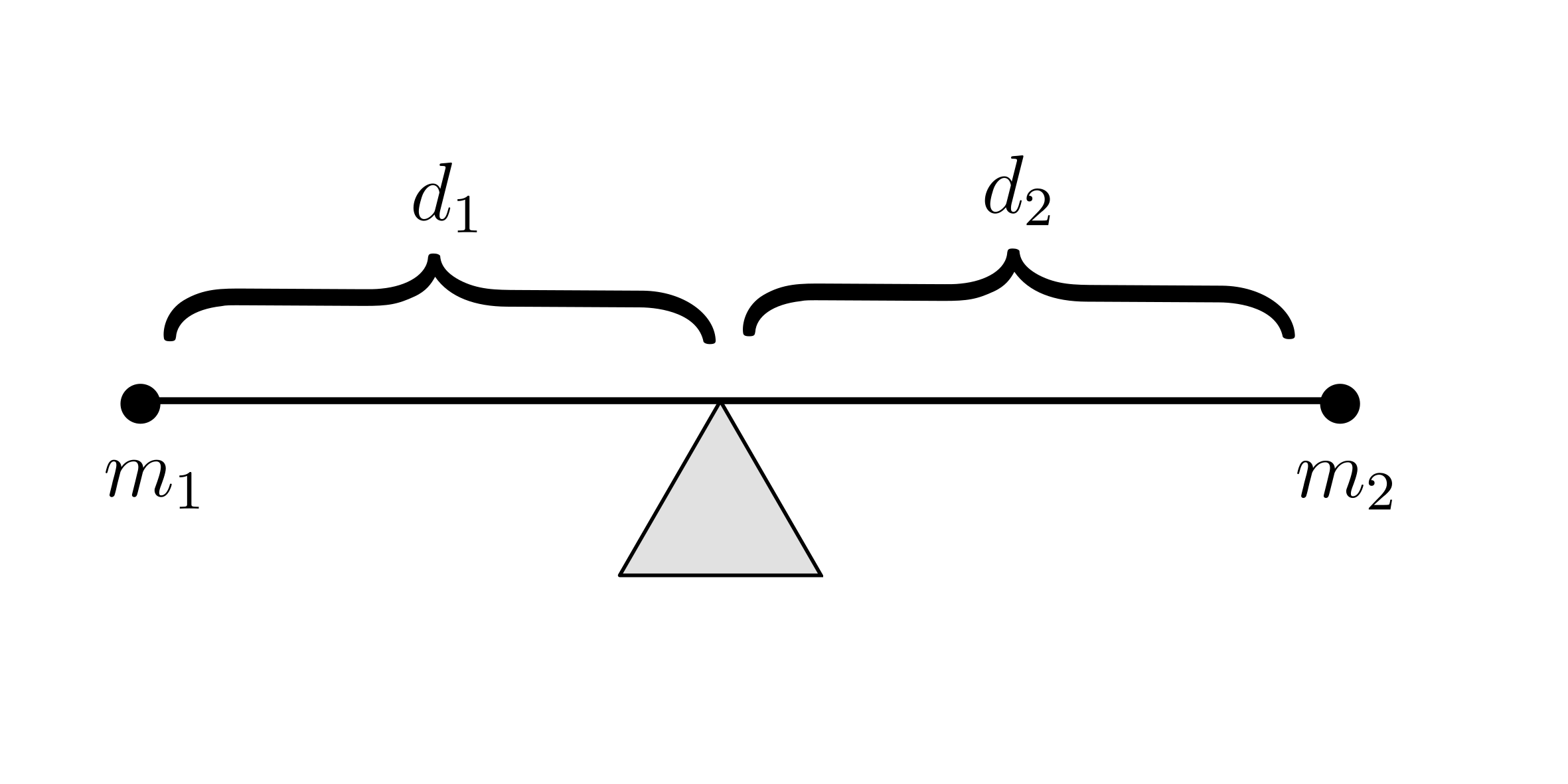
$m_1d_1 = m_2d_2$

Now suppose that rod lied along the x-axis.

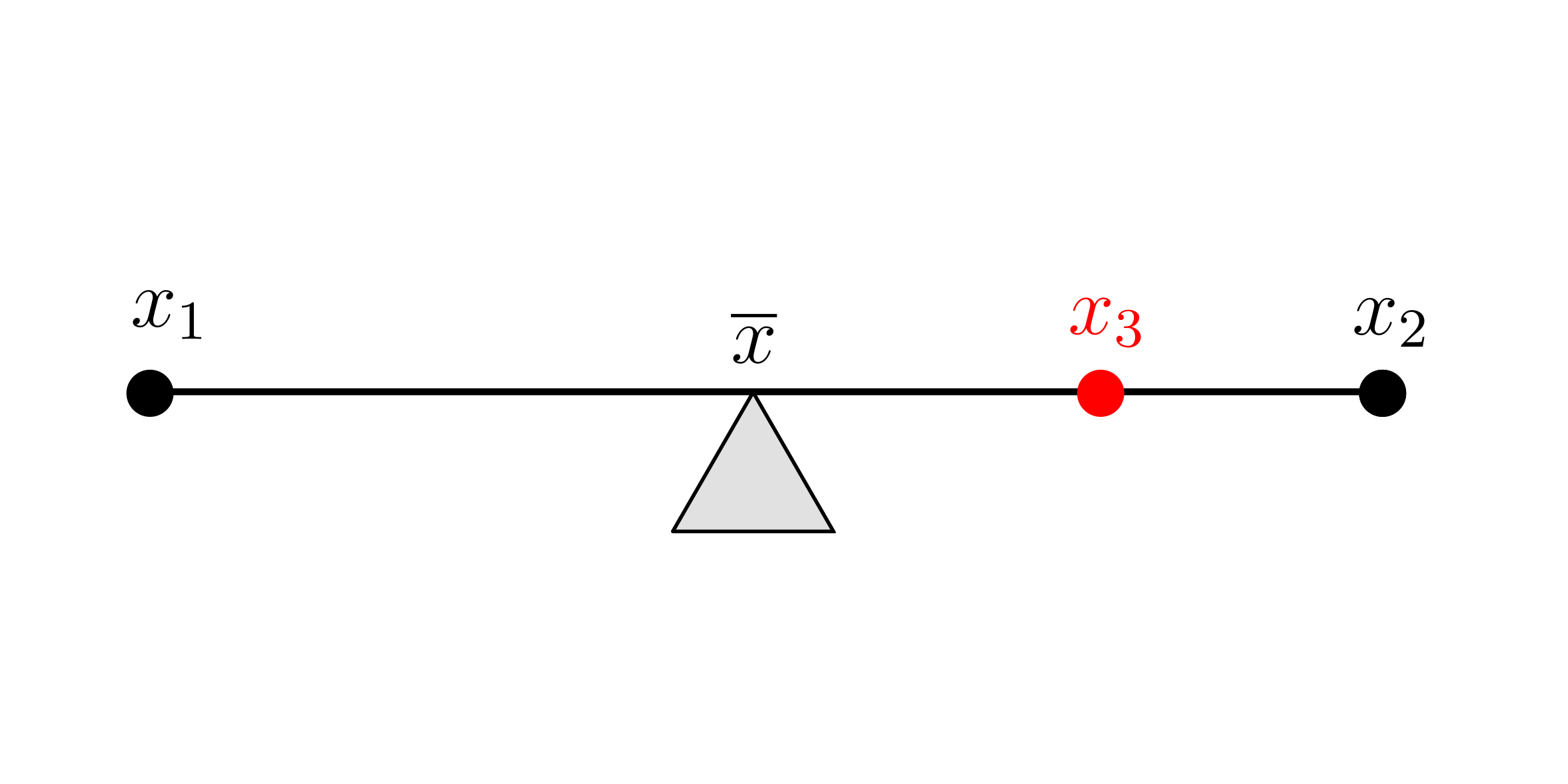
$d_1 = \bar{x} - x_1$

$d_2 = x_2 - \bar{x}$

$m_1d_1 = m_2 d_2 \implies m_1 \left( \bar{x} - x_1 \right) = m_2 \left( x_2 - \bar{x} \right)$

$= m_1 \bar{x} - m_1 x_1 = m_2 x_2 - m_2 \bar{x}$

$= \bar{x} \left( m_1 + m_2 \right) = m_1 x_1 + m_2 x_2$

$= \bar{x} = \frac{m_1x_1 + m_2 x_2}{m_1 + m_2}$

Or with the third point:

$m_1 (\bar{x} - x_1) = m_2 \left( x_2 - \bar{x} \right) + m_3 \left( x_3 - \bar{x} \right)$

$m_1 \bar{x} - m_1 x_1 = m_2 x_2 - m_2 \bar{x} + m_3 x_3 - m_3 \bar{x}$

$\bar{x} = \frac{m_1 x_1 + m_2 x_2 + m_3 x_3}{m_1 + m_2 + m_3}$

Where $m_1 x_1$ and $m_2x_2$ are called the moments of the masses $m_1$ and $m_2$ with respect to the origin. The equation suggests that the center of mass $\bar{x}$ is obtained by adding the moments and dividing by the total mass $m = m_1 + m_2 + …$.

To generalize for a system of $n$ particles with masses $m_1,\ m_2,\ …,\ m_n$ located at the points $x_1,\ x_2,\ …,\ x_n$ on the x-axis it can similarly be shown that the center of mass of the system is given by

$\bar{x} = \frac{\sum_{i=1}^{n} m_i x_i}{\sum_{i=1}^{n} m_i} = \frac{M_x}{M}$ where

$M = \sum_{i=1}^{n} m_i$ is the total mass of the system and

$M_x = \sum_{i=1}^{n} m_i x_i$ is the sum of the moments of the system.

Suppose we have a 1D object, laid along the x-axis between $x=a$ and $x=b$ with a continuous density $\delta _l (x)$. Then the x-component of the moment is

$M_x = \int_{a}^{b} x dm$

$M_x = \lim_{n \to \infty} \sum_{i=1}^{n} x_i m_i = \lim_{n \to \infty} \sum_{i=1}^{n} x_i \Delta m_i = \int_{a}^{b} x dm$

$dm = \delta_{L}(x) dx$

$dm = \delta _{\text{Area}} (x) dA = \delta _{\text{Area}} (x) h(x) dx$

$= \int_{a}^{b} x \delta_L (x) dx$

$M = \int_{a}^{b} dm$

$= \int_{a}^{b} \delta _{l}(x) dx$

$\bar{x} = \frac{M _x}{M} = \frac{\int _{a}^{b} x \delta _L (x) dx }{\int _{a}^{b} \delta _L (x) dx }$

We can only work with 2D because 3D requires multi-variable calculus. However, if the shape is symmetrical, we can in Calculus 2.

Consider a flat plate:

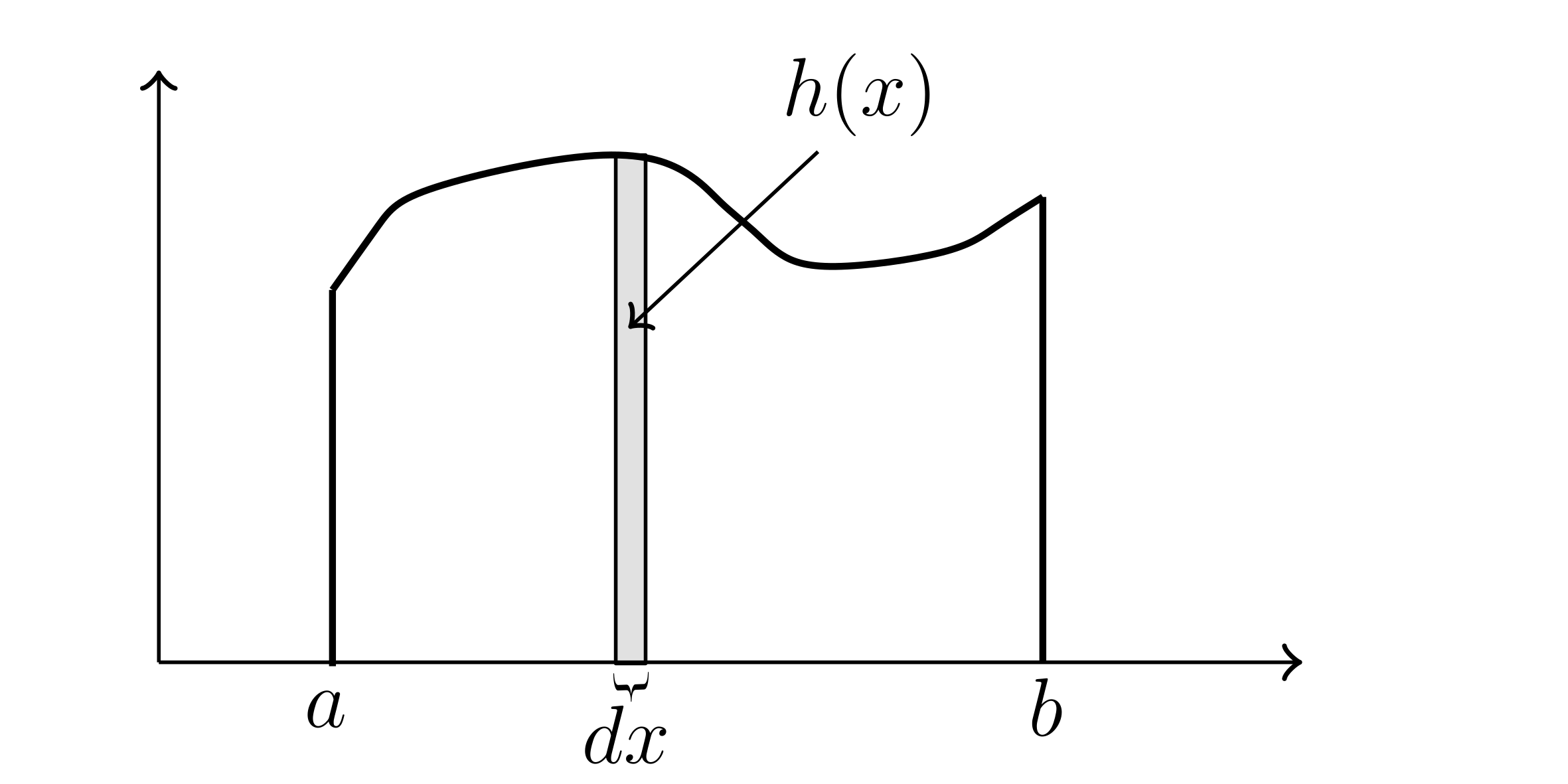
Consider plate with density $\delta _{\text{Area}}(x)$. We wish to locate center of mass of this plate. If we assume we have a function $f(x)$ which gives height of the cross section of the object, then we know that infinitesimally wide vertical slab has a mass given by:

$d m = \delta _{\text{Area}} (x) dA = \delta _{\text{Area}}(x) h(x) dx = \delta _{\text{Area}}(x) f(x) dx$

In addition, the contribution of this slab of mass to the $x$-component of the moment will be $x dm = x \delta _{\text{Area}}(x) f(x) dx$ and the x-component of the moment is:

$M_x = \int_{x=a}^{x=b} x dm = \int_{a}^{b} x \delta _{\text{Area}}(x) f(x) dx$

The total mass of the object is $M = \int_{a}^{b} d m = \int_{a}^{b} \delta _{\text{Area}}(x) f(x) dx$

If we have a plate on the xy plane, lying between lines $x=a$ and $x=b$ under graph $y=f(x)$ and above graph $y=g(x)$

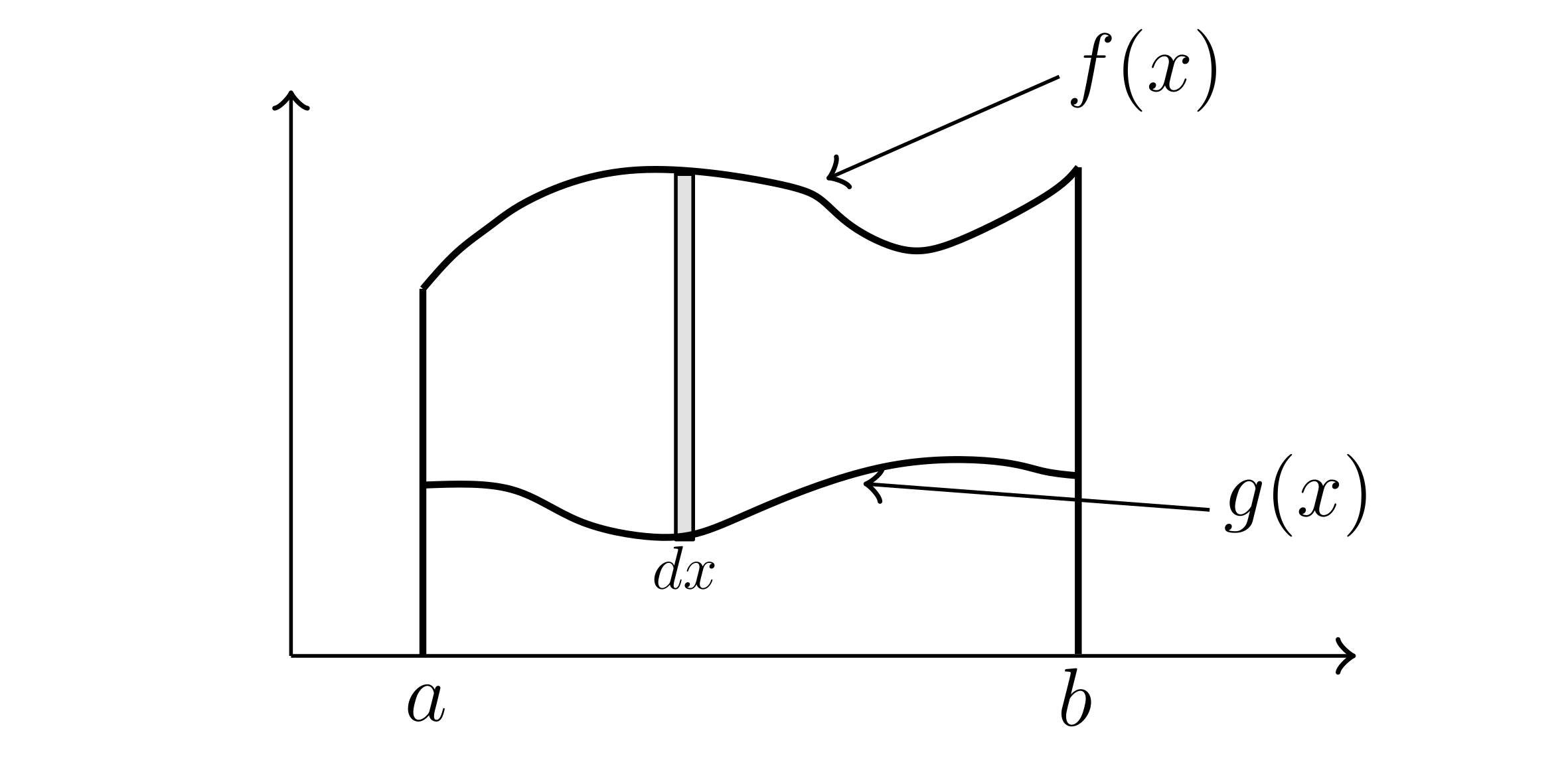
$f(x) \ge g(x)$ on $[a,\ b]$

Then the total mass is

$M = \int _{a}^{b} \delta _{\text{Area}}(x) h(x) dx$

$dA = h(x) dx$

$M = \int_{a}^{b} \delta _{\text{Area}}(x) \left( f(x) - g(x) \right) dx$

The x-component is:

$M_x = \int_{a}^{b} x \delta _{\text{Area}}(x) \left( f(x) - g(x) \right) dx$

$\bar{x} = \frac{\int _{a}^{b} x\delta _{\text{Area}}(x) \left( f(x) - g(x) \right) dx}{\int _{a}^{b} \delta _{\text{Area}}(x) \left( f(x) - g(x) \right) dx }$

As far as y-component of the moment, we have:

$M_y = \int_{a}^{b} \frac{f(x) + g(x)}{2} \delta_{\text{Area}}(x) \left( f(x) - g(x) \right) dx$

$M = \int_{a}^{b} \delta _{\text{Area}}(x) \left( f(x) - g(x) \right) dx$

Example:

The region is bounded by $y=x^2$, above $y=1$, and $x=2$.

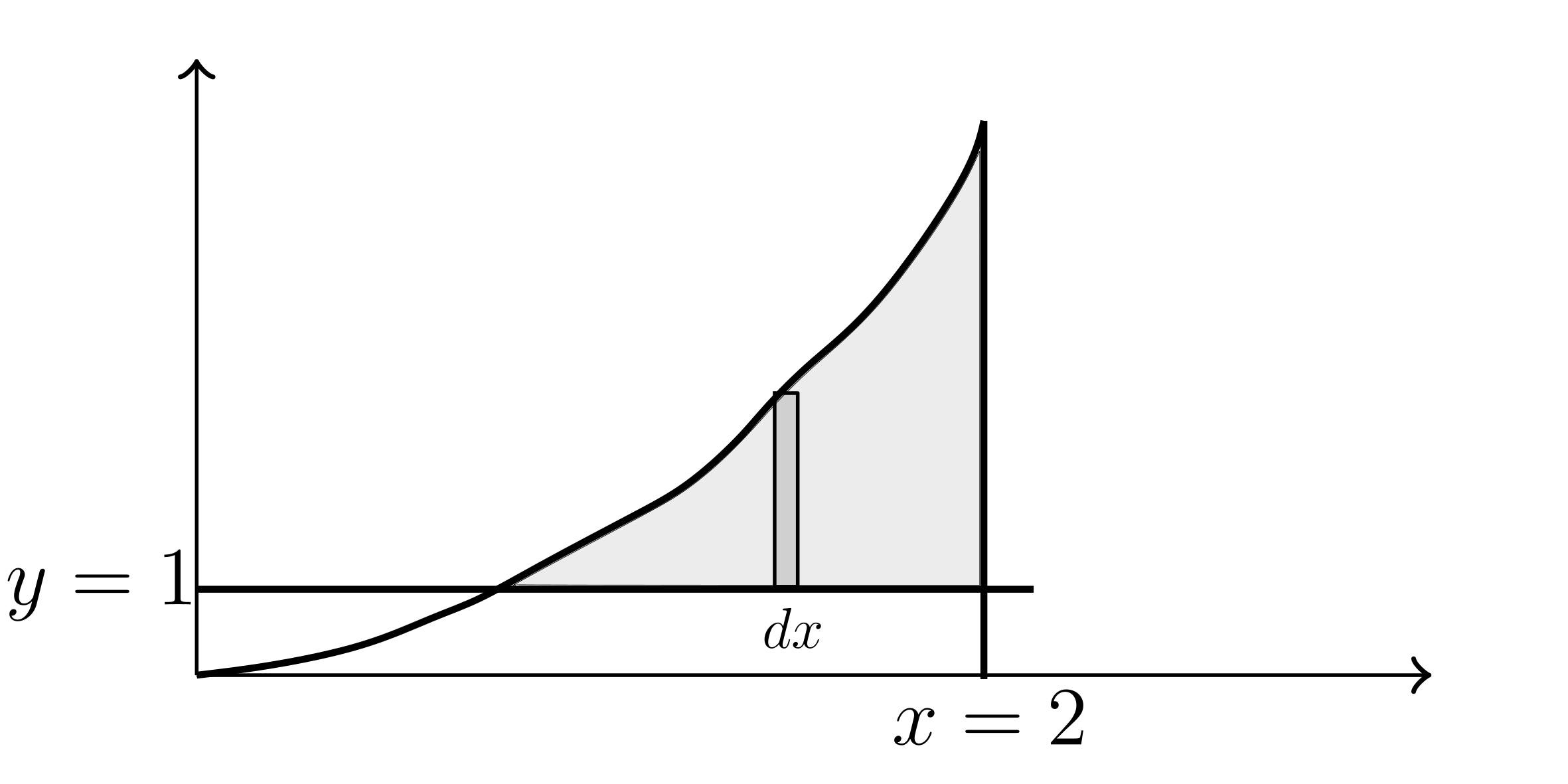
Find the center of mass of the plate if $\delta _{\text{Area}}(x) = x$.

$M = \int \delta _{\text{Area}}(x) dA$

$dA = h(x) dx$

$dA = \left( y^T - y^B\right) dx = \left( x^{2}-1 \right) dx$

$M = \int_{0}^{2} x \left( x^2 - 1 \right) dx = \frac{9}{4}$

$M_x = \int_{1}^{2} x \delta _{\text{Area}}(x) \left( x^{2}-1 \right) dx$

$M_x = \int_{1}^{2} x x \left( x^2 - 1 \right) dx = \frac{58}{15}$

$M_y = \int_{1}^{2} \frac{x^2 + 1}{2} \delta _{\text{Area}}(x) \left( x^2 - 1 \right) dx$

$M_y = \int_{1}^{2} \frac{x^4-1}{2}x dx = \frac{9}{2}$

Thus, $\bar{x} = \frac{M_x}{M} = \frac{\frac{58}{15}}{\frac{9}{4}} \approx 1.7185$

$\bar{y} = \frac{M_y}{M} = \frac{\frac{9}{2}}{\frac{9}{4}} = 2$

For the exam, you only need to setup the integral, you don’t need to solve it.

Example:

$f(x) = x$, $g(x) = x^{2}$, $\delta _{\text{Area}}(x) = 2x + 1$

$M = \int _{0}^{1} \delta _{\text{Area}}(x) h(x) dx = \int _{0}^{1} (2x+1) \left( f(x) - g(x) \right) dx$

$M = \int_{0}^{1} (2x+1)(x^2-x) dx = \frac{1}{3}$

$M_x = \int _{0}^{1} x \delta _{\text{Area}}(x) h(x) dx = \int _{0}^{1} x (2x+1) \left( x^{2} - x \right) dx = \frac{11}{60}$

$M_y = \int_{0}^{1} \frac{f(x) + g(x)}{2} \delta _{\text{Area}}(x) \left( f(x) - g(x) \right) dx$

$M_y = \int_{0}^{1} \frac{x+x^2}{2}(2x+1) \left( x-x^2 \right) dx = \frac{3}{20}$

$\overline{x} = \frac{M_x}{M} = \frac{\int_{0}^{1} x(2x+1)(x-x^2) dx}{\int_{0}^{1} (2x+1)(x-x^2) dx}$ (This is all that’s required in the exam).

$\overline{y} = \frac{M_y}{M} = \frac{\int_{0}^{1} \frac{x+x^2}{2} (2x+1)\left( x-x^2 \right) dx }{\int_{0}^{1} (2x+1)\left( x-x^2 \right) dx }$

Example:

Find the center of mass for $f(x) = 3x+5$, $g(x) = x-3$, $x=-4$ (redundant), $\delta _{\text{Area}}(x) = x^{2}+3$.

$M_x = \int_{-4}^{3} x(x^2+3)((3x+5)-(x+3)) dx$

$M_x = \int_{-4}^{3} x\left( x^{2}+3 \right) \left( 2x+8 \right) dx$

$M = \int_{-4}^{3} \left( x^{2}+3 \right) \left( 2x+8 \right) dx$

$M_y = \int_{-4}^{4} \frac{4x+2}{2} \left( x^{2}+3 \right) \left( 2x+8 \right) dx$

$\overline{x} = \frac{M_x}{M} = \frac{\int_{-4}^{3} x \left( x^2+3 \right) (2x+8) dx}{\int_{-4}^{3} \left( x^2+3 \right) \left( 2x+8 \right) dx}$

$\overline{y} = \frac{\int_{-4}^{3} \left( 2x+1 \right) \left( x^2 + 3 \right) \left( 2x+8 \right) dx }{\int_{-4}^{3} \left( x^2+3 \right) \left( 2x+8 \right) dx}$

Work and Energy

We will focus on work done by emptying fluid.

Consider a spring force:

Hooke’s Law:

$F_{\text{Spring}} = -kx$ (Case of stretching)

$F _\text{Compression} = kx$ (Case of compression)

Example:

What is the work done by emptying fluid from this container:

You have water filling up this container up to 10 feet.

$\delta _{\text{Water}} = 62.4 \frac{\text{lb}}{\text{ft}^{2}}$

Find the work ($W$) done to empty this container.

$dV = A(t) dz = 8 (20) dz = 160 dz$

$dm = \delta dV$

$dF = g dm = g \delta _{\text{Water}} dv$

$dF = g \delta _{\text{Water}} 160 dz$

$W = dF \times \text{Distance} = \left( 30-z \right) dF$

$W = \int_{0}^{10} \left( 30-z \right) dF = \int_{0}^{10} \left( 30-z \right) g \delta _{\text{Water}} 160 dz$

$W = \int_{0}^{10} \left( 30-z \right) g (62.4) (160) dz$ (All you need to get to on the exam)

Example:

$\delta _{\text{Water}} = 62.4 \frac{\text{lb}}{\text{ft}^2}$

Consider the cone below:

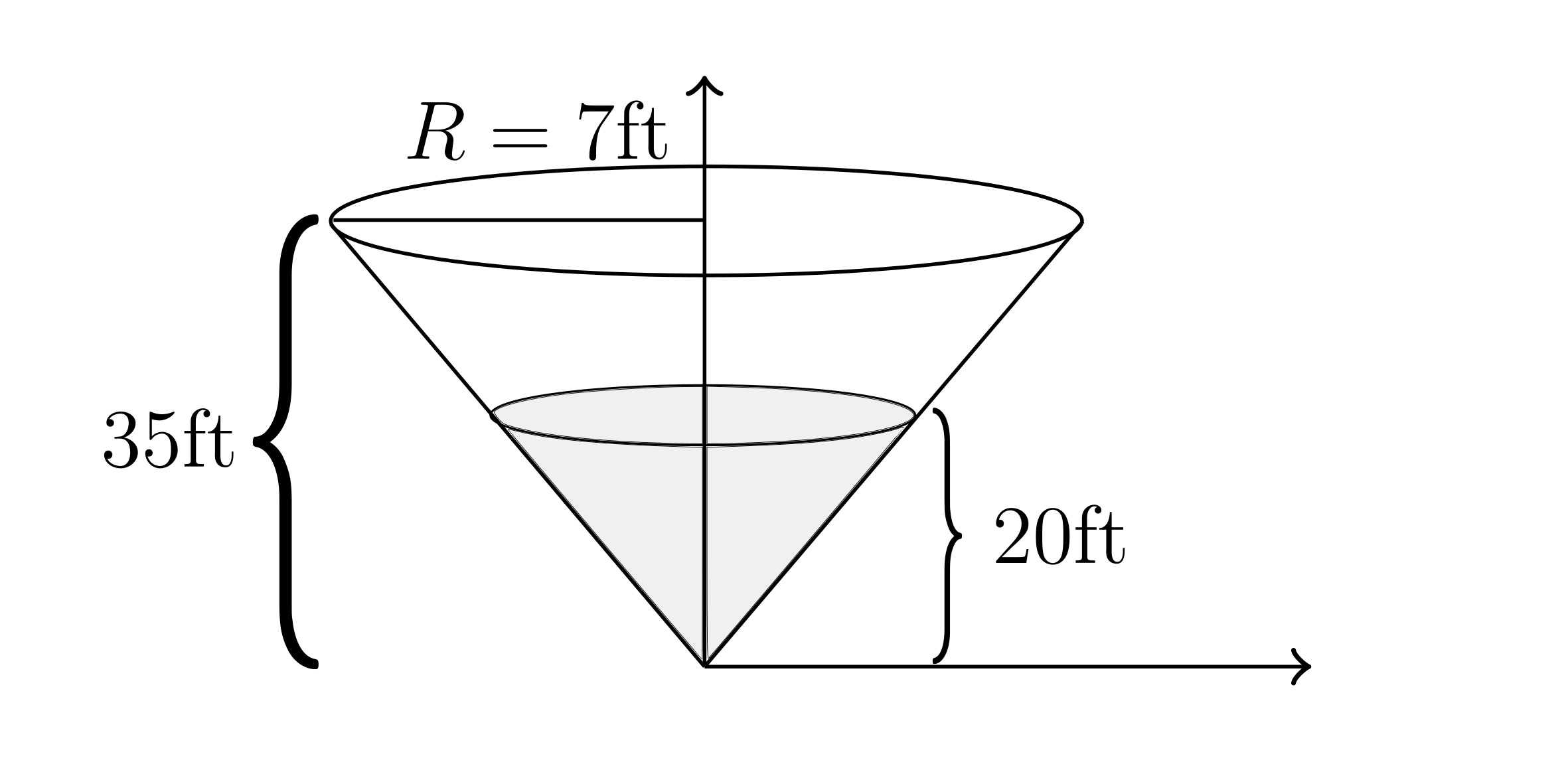
$dV = A(y) dy$

$A(y) = \pi R(y)^2$

Consider a cross-section of the cone:

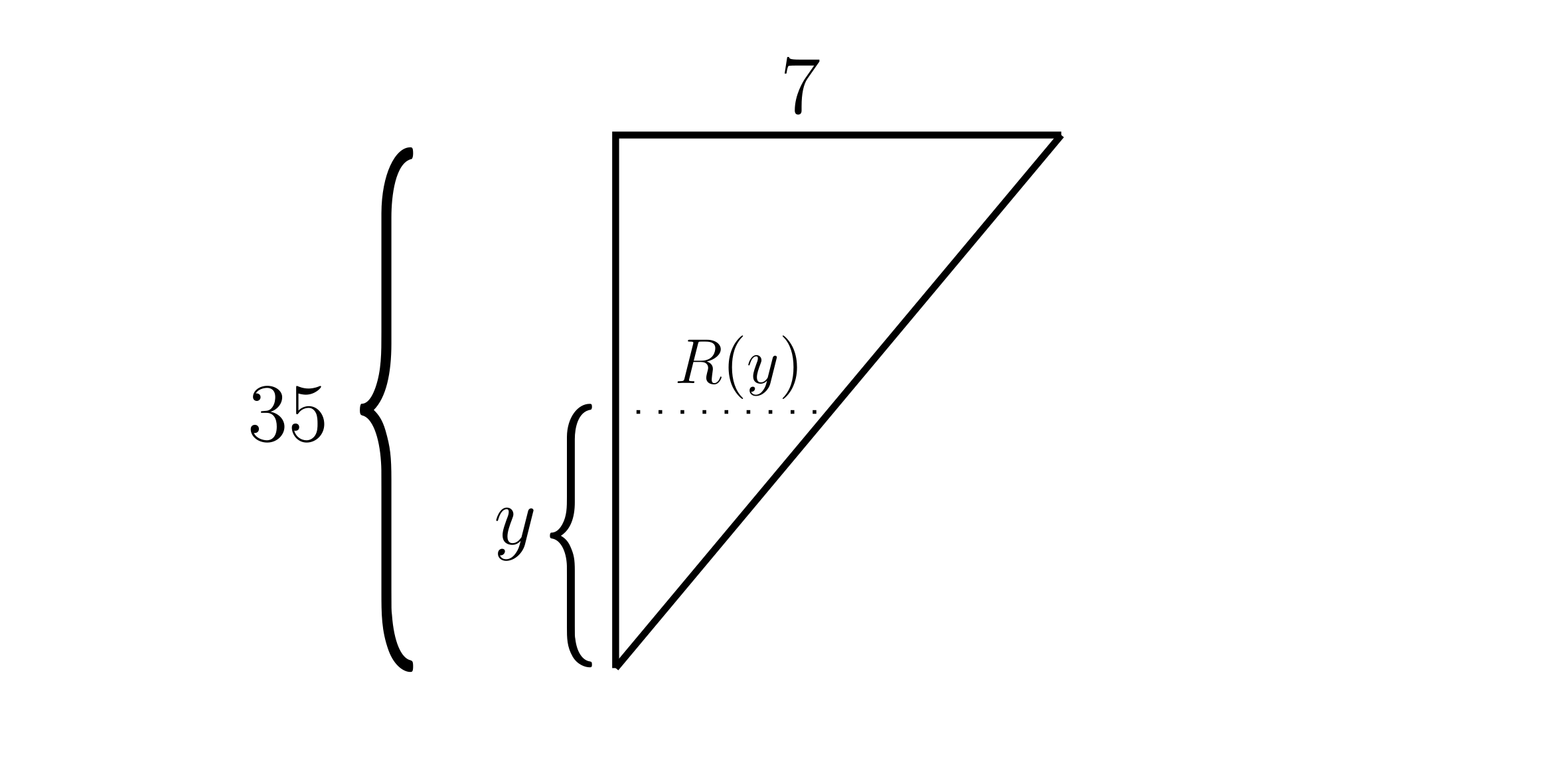
$\frac{R}{y} = \frac{7}{35}$ (because they are similar triangles)

$\therefore R = \frac{7y}{35}$

$A(y) = \pi \left( \frac{7y}{35} \right)^{2}$

Hence $dV = \pi \left( \frac{y}{5} \right) ^{2} dy$

$dF = g dm \implies dF = g \delta _{\text{Water}} dV$

$dF = g (62.4) \pi \left( \frac{y}{5} \right)^{2} dy$

$w = \int_{0}^{20} \left(35-y \right) dF$

$w = \int_{0}^{20} \left( 35-y \right) g (62.4) \pi \left( \frac{y}{5} \right)^{2} dy$

---

Exam 1:

• 10:00am - 11:30am
• 7 Questions
  • #1 - Partial Fractions
  • #1 - Integration: Substitution or By Parts
  • #2 - Improper Integral: Does it converge (if so, give value) or diverge?
  • #3 - Approximate integral via Simpsons Rule (n=4)
  • #4 - Distance and/or Displacement (evaluate) and magnitude
  • #5 - Volume with hint of method (setup only!)
  • #6 - Center of Mass: shifted axis. Shade the region. Find points of intersection. Suppose a thin metal plate. (setup only!)
    • Mass of the plate
    • X chord of center of mass
    • Y chord of center of mass
  • #7 - Work (setup only!)

---

Exam 1 Review

Rotate $y=x^2 +3$, $y=1$, $x=0$, $x=3$ about $x=-2$ using the shell method.

• We used the shell method instead of disk method because disk method would be in two steps.

Approximating Polynomials

Consider this first-order approximation on a second-order function:

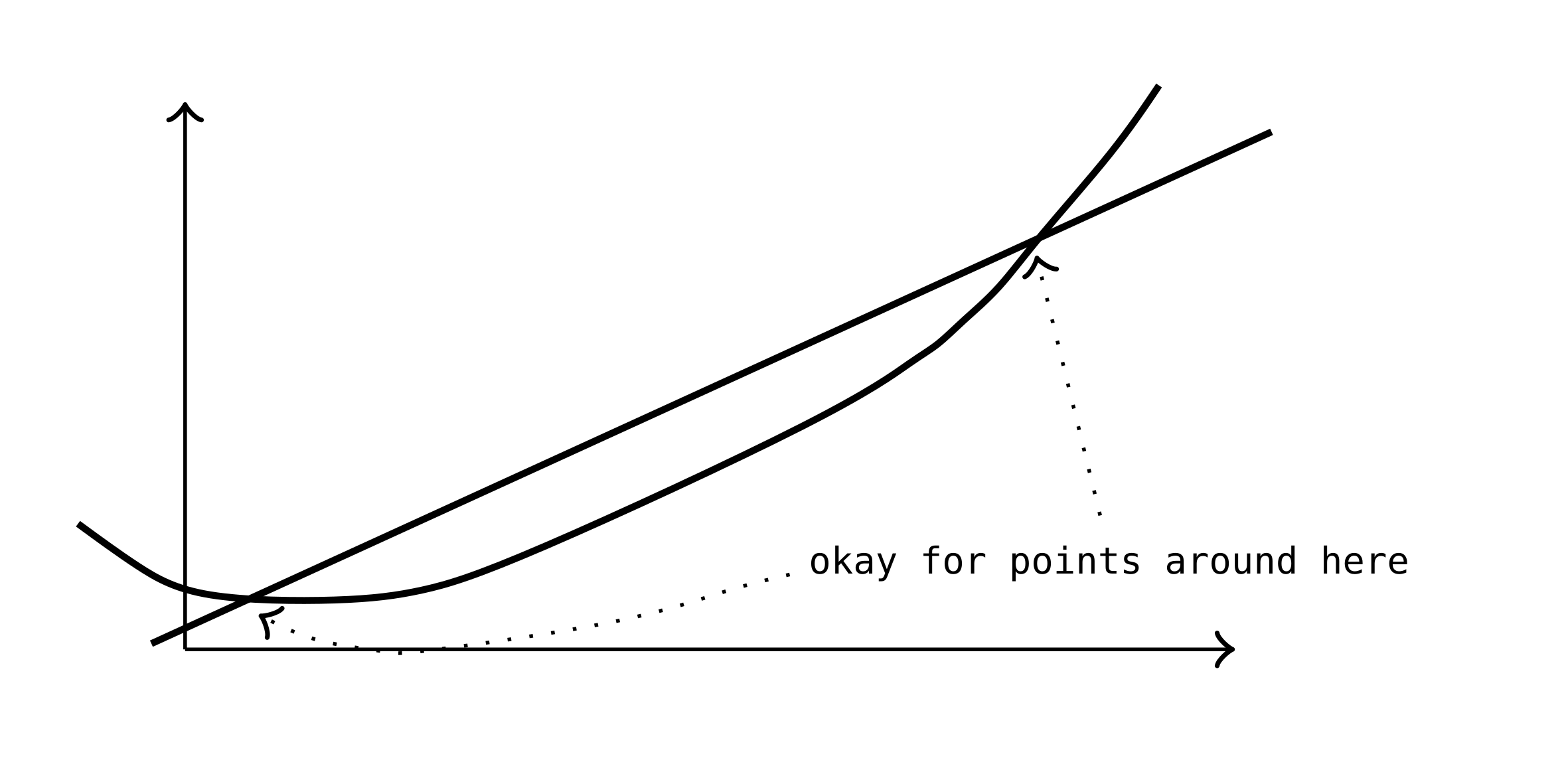
Now we can focus the approximation on a certain point $x=a$:

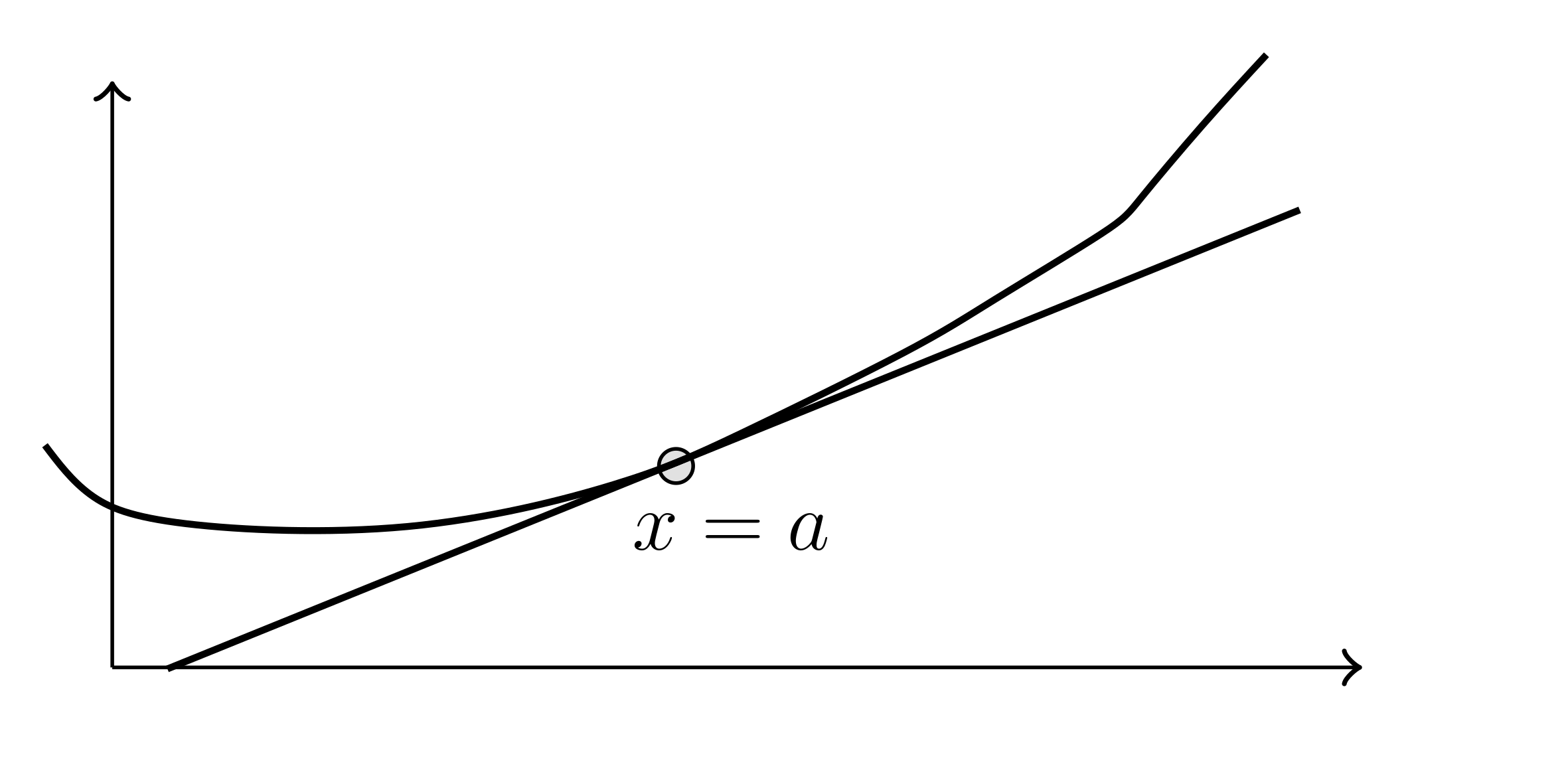
Linear approximation: $L(x) = f(a) + f^{\prime}(a)(x-a)$

Example

Approximate $y=\ln x$ near $x=e$

$L(x) = f(e) + f’(e)(x-e) = 1 + \frac{1}{e}(x-e) = \frac{x}{e}$

What about near $x=3$?

$L(3) = \frac{3}{e} \approx 1.103$

$\ln 3 \approx 1.098$

$\ln 2.9 \approx 1.064710$

$L(2.9) = \frac{2.9}{e} \approx 1.0668$

Second-order approximations:

$L(x) = f(a) + f’(a)(x-a) + \frac{f’‘(a)}{2!}(x-a)^2$

Third-order approximations:

$L(x) = f(a) + f’(a)(x-a) + \frac{f’‘(a)}{2!}(x-a)^2 + \frac{f’‘(a)}{3!}(x-a)^3$

A general polynomial function, in power of $x$ is defined as follows:

$p(x) = c_0 + c_1 x + c_2 x^2 + … + c_d x^d = \sum_{k=0}^{d} c_k x^k$

Where $d$ is the degree of polynomial.

When $x$ is close to zero, a polynomial $p(x)$ can be approximated “well” by leaving off (or dropping) the terms of the form $x^k$, where $k$ is large.

This polynomial in the above formula was centered at a or about a where $a=0$. Sometimes we want to have polynomial centered at any other number. That is, we want our original polynomial to be written in powers of $(x-a)$. Then we have out definition:

A polynomial centered at $a$ is a polynomial written in terms of powers $(x-a)$ in the following form:

$q(x) = b_0 + b_1 (x-a) + b_2 (x-a) + … + b_d (x-a)^d = \sum_{k=0}^{d} b_k (x-a)^k$

Example:

$p(x) = 4 - x + 5x^2 + 9x^5$

When $x$ is close to 0, the 0 degree term, 4, is the most important, $-2x$ is the second most important, $5x^2$ is the third important, and $9x^5$ is the least important if $x$ is close to zero.

Let’s assume the notation that $p^n(x)$ means the sum of all of the first $n$ terms of the polynomial. Hence, on the previous example:

$P^0(x) = 4$

$P^1(x) = 4-2x$

$p^2(x)=4-2x+5x^2$

$p^3(x)=4-2x+5x^2$

$p^4(x)=4-2x+5x^2$

$p^5(x)=4-2x+5x^2+9x^5$

Example:

Again, $p(x) = 4-2x+5x^2+9x^5$.

If $x$ is close to zero, then what power of $x$ best approximates $\frac{1}{5}\left( p(x) - r + 2x \right)$?

Solution:

We find that $\frac{1}{5}\left( p(x) -4+2x \right) =x^2+\frac{9}{5}x^5$

2nd power best approximates it because $\frac{9}{5}x^5$ is very small.

Example:

$p(x) = 1-x+2x^2-3x^3+4x^4$

If $x$ is close to zero, what power of $x$ best approximates $\frac{1}{3} \left( p(x) - 1 + x - 2x^2 \right)$?

Follows that $\frac{1}{3}\left( p(x)-1+x-2x^2 \right) =-x^3 + \frac{4}{3}x^4$

Therefore, the 3rd power of x best approximates this.

Example:

Let $p(x) = 4-2x+5x^2+9x^5$ and we want to approximate $p(x)$ by another polynomial $p(x)$, which is centered at $a=1$, namely we want to find $p(x) = b_0 + b_1(x-1) + b_2(x-1)^2 + b_3(x-1)^2+b_4(x-1)^4 + b_5(x-1)^5$. That is, we want to find $b_0,\ b_1,\ b_2,\ b_3,\ b_4,\ b_5$.

To find constants $b_i$, we use the approach:

Solution:

$p(1) = b_0 \implies q(1) = 4 - 2 + 5 + 9 = 16$

So $b_0 = 16 = \frac{p^0(1)}{0!}$

$p’(x) = b_1 + 2b_2 (x-1) + 3b_3 (x-1)^2 + 4b_4(x-1)^3 + 5b_5 (x-1)^4$

$p’(1) = b_1 \implies p’(x) = -2 + 10x+45x^4 \implies p’(1) = -2 + 10 +45 = 53$

So $b_1 = 53$ and $b_1 = \frac{p’(1)}{1!}$

$p’‘(x) = 2b_2 + 2(3) b_3 (x-1) + 3(4) (x-1)^2 + 4 (5) b_5 (x-1)^3$

$p’‘(1) = 2b_2$

So $b_2 = \frac{p’‘(1)}{2} = \frac{p’‘(1)}{2!} = 190$

$p’‘(x) = 10 + 180x^3$

$p’‘(1) = 10 + 180 + 190$

$\therefore 2b_2 = 190 \implies b_2 = 95$

$p’’‘(x) = 2(3)b_3 + 2(3)(4)(x-1) + 3(4)(5)(x-1)^2$

$p’’‘(1) = 2(3)b_3$

$b_3 = \frac{p’’‘(1)}{3!}$

$p’’‘(x) = 540x^2$

$p’’‘(1) = 540$

$6b_3 = 540 \implies b_3 = \frac{540}{6} = 90$

$p^{(4)}(x) = p’’’‘(x) = 2(3)(4) + 2(3)(4)(5)(x-1)$

$p^{(4)}(1) = 2(3)(4)b_4$

$b_4 = \frac{p^{(4)}(1)}{4!}$

$p^4(x) = 1080x$

$p^{(4)}(x) = 1080$

$4! b_4 = 1080 \implies b_4 = \frac{1080}{4!} = 45$

$p^{(5)}(x) = 5! b_5$

$p^{(5)}(1) = 5! b_5$

$b_5 = \frac{p^{(5)}(1)}{5!}$

$p^{(5)}(x) = 1080$

$b_5 = \frac{1080}{5!} = 9$

$p(x) = 16 + 53(x-1)+95(x-1)^2 + 95(x-1)^3 + 45(x-1)^4 + 9(x-1)^5$

$p(x) = 4-2x+5x^2+9x^5$

Note that these are the exact same at $x=1$ and $x=-1$.

Example:

$p(x) = (x-1)^3$, find $q(x)$ centered at $a=0$.

$q(x) = b_0 + b_1 x + b_2x^2 + b_3x^3$

$b_k = \frac{p^{(k)}(a)}{k!}$

$b_0 = \frac{p^{(0)}(0)}{0!} = -1$

$b_1 = \frac{p^{(1)}(0)}{1!} = \frac{3}{1!} = 3$

$b_2 = \frac{p^{(2)}(0)}{2!} = \frac{-6}{2!} = -3$

$b_3 = \frac{p^{(3)}(0)}{3!} = \frac{6}{3!} = 1$

$q(x) = -1 + 3x - 3x^2 + x^3$

Example:

$y=x^2$ centered around $a=9$

$q(x) = c_0 + c_1(x-9) + c_2(x-9)^2$

DNF

Example:

$q(x) = a_0 + a_1 x + a_2 x^2 + a_3 x^3 + a_4 x^4 + … + a_n x^n$

$q^{n}(x)$ is the partial form of the $n$-th order approximation

i.e $q^{2}(x) = a_0 + a_1 x + a_2 x^2$

$q^{0}(x) = a_0$

General form is $q(x) = a_0 + a_1(x-a) + a_2 (x-a)^2 + … a_n (x-a)^n$

$b_k = \frac{p^{(k)}(a)}{k!}$

Remember that $p^{(k)}$ means the $k$-th derivative of $p$.

Error

Error is always absolute value (always positive)

Error in approximating $q(x)$ by it’s $n$-th order partial sum $q^{n}(x)$. The difference between them is called the remainder and defined $R^{n}(x)$ so that $R^{n}(x) = q(x) - q^{n}(x)$

The error $E^{n}(x)$ is $E^{n}(x) = \mid R^{n}(x) \mid = \mid q(x) - q^{n}(x) \mid$

Example:

$q(x) = 7+3(x+2) - 5(x+2)^4$

What is the max error that we have in approximating $q(x)$ by $q^1(x)$ by first-order partial sum?

$q^{1}(x) = 7 + 3(x+2)$

$E^{1}(x) = \mid q(x) - q^{1}(x) \mid = \mid - 5 (x+2)^4 \mid$

$E^{1}(x) = 5 \mid x+2 \mid ^{4}$

If we suppose that $x$ is within 0.1 of -2, then $\mid x+2 \mid \le 0.1$. Hence $E^{1}(x) = 5 \mid x+2 \mid ^{4} \le 5.0 (0.1)^{4} = 0.0005$

Example:

$q(x) = x^2 + 5x + 6$

Rewrite $q(x)$ centered at $a=-2$

$q(x) = b_0 + b_1 (x+2) + b_2 (x+2)^2$

$b_n = \frac{q^{(n)}(a)}{n!} = \frac{q^{(n)}(-2)}{n!}$

$b_0 = \frac{q^{(0)}(-2)}{0!} = \frac{(-2)^2+5(-2)+6}{0!} = \frac{4-10+6}{0!} = 0$

$b_1 = \frac{q^{(1)}(-2)}{1!} = \frac{2x+5}{1!} = \frac{1}{1!} = 1$

$b_2 = \frac{q^{(2)}(-2)}{2!} = \frac{2}{2!} = 1$

$\therefore q(x) = (x+2) + (x+2)^2 = x^2 + 5x +6$

Example:

$f(x) = x^3 - 3x^2 + 3x - 1$ centered at $x=1$

$a_0 = \frac{f(1)}{0!} = \frac{0}{0!} = 0$

$a_1 = \frac{f^{(1)}(1)}{1!} = \frac{0}{1!} = 1$

$a_2 = \frac{f^{(2)}(1)}{2!} = \frac{1}{2!} = 1$

$f(x) = (x-1)^3$

Example:

$q(x) = 1-x+2x^2 - 3x^3 + 4x^4$ centered at $a=1$

$q(x) = \sum_{k=0}^{\infty} b_k (x-1)^k = b_0 + b_1 (x-1) + b_2 (x-1)^2 + b_3 (x-1)^3 + b_4 (x-1)^4$

Do this work. You should get:

$q(x) = 3+10(x-1) + 17(x-1)^2 + 13 (x-1)^3 + 4(x-1)^4$

Example:

Approximate $q(x) = x^2 + 5x + 6$ at $x=-2.1$ by using the re-centered 1st order partial sum.

Recall from above that the re-centered polynomial is $q(x) = (x+2) + (x+2)^2$

$q^{1}(x) = x+2$ first-order partial sum

So $q^{1}(x) = -2.1 + 2 = -0.1$

$q(-2.1) = -0.09$

$E^{1}(x) = \mid q(x) - q^{1}(x) \mid = \mid x^{2} \mid$

$E^{1}(-2.1) = \mid -0.09 - (-0.1) \mid = 0.01$

For $n$ big enough, we expect that $T _{f}^{n}(x;\ a)$ approximates $f(x)$ well when $x$ is near $a$.

Note that first-order Taylor polynomial is $T _{f}^{1} (x,\ a) = f(a) + f’(a)(x-a)$ which is linearization of $f(x)$ at $a$. That is $L _{f}(x,\ a)$.

Example:

Let $f(x) = e^{x}$. Find $T _{f} ^{n}(x)$, the $n$-th order Taylor polynomial centered at $a=0$. Use first and third order polynomial to approximate $e^{0.1}$ and compare this approximation with the calculator value.

$T _{f} ^{n} (x) = \sum _{k=0}^{n} \frac{f^{(k)}(x)}{k!} = 1+x+\frac{x^2}{2!}+\frac{x^3}{3!} + … + \frac{x^{n}}{n!}$

$e^x \approx T _{f}^{n}(x) = \frac{f(0)}{0!} + \frac{f’(0)}{1!} + \frac{f’‘(0)}{2!} x^2 + \frac{f’’‘(0)}{3!} + … + \frac{f^{(n)}(0)}{n!} x^{n}$

$f(x) = e^{x}$

$f^{(n)}(x) = e^{x}$

$\frac{f(0)}{0!} = \frac{1}{0!} = 1$

$\frac{f’(0)}{1!} = \frac{1}{1!} = 1$

$\frac{f’‘(0)}{2!} = \frac{1}{2!} = \frac{1}{2}$

$e^{x} = T _{f}^{n}(x) = 1 + x + \frac{x^{2}}{2!} + \frac{x^3}{3!} + … + \frac{x^n}{n!}$

$T _{f}^{1} (x) = 1 + x$

$T _{f} ^{1} (0.1) = 1 + 0.1 = 1.1$

$T _{f}^{3}(x) = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!}$

$T _{f}^{3} (0.1) = 1 + 0.1 + \frac{0.1^{2}}{2!} + \frac{0.1^{3}}{3!} \approx 1.1051666$

$e^{0.1} = 1.105170918$

For practice, do $e^{x}$ at $a=-1$.

Example:

Recall that $T _{f} ^{\infty} (x;\ a) = T _{f} (x;\ a)$

$= c _{o} c_1 (x-a) + c_2 (x-a)^2 + c_3 (x-a)^3 + … + c_n (x-a)^n$

$= \sum_{n=0}^{\infty} c_n (x-a)^n$ where $C_n = \frac{f^{(n)}(a)}{n!}$

Let’s find T.S. for $f(x) = \sin x$ centered at $R = pi/2$

$T _f (x;\ \frac{\pi}{2}) = c_0 + c_1 (x-\frac{\pi}{2}) + c_2 (x-\frac{\pi}{2})+ c_3 (x-\frac{\pi}{2}^3) + …$

$f(x) = \sin x$

$f’(x) = \cos x$

$f’‘(x) = -\sin x$

$f’’‘(x) = -\cos x$

$f^{(4)}(x) = \sin x$

Therefore the derivative at $\frac{\pi}{2}$ are 1, 0, -1, 0, 1, 0, -1, 0,… and so T.S. centered at $\frac{\pi}{2}$ is:

$F _f (x;\ \frac{\pi}{2}) = 1 - \frac{\left( x-\frac{\pi}{2} \right) ^{2}}{2!} + \frac{\left( x-\frac{\pi}{2} \right) ^{4}}{4!} - \frac{\left( x-\frac{\pi}{2} \right) ^{6}}{6!} + \frac{\left( x - \frac{\pi}{2} \right) ^{8}}{8!} - \frac{\left( x-\frac{\pi}{2} \right) ^{10}}{10!}$

$= \sum_{n=0}^{\infty} (-1)^{n+2} \frac{\left( x-\frac{\pi}{2} \right)^{2n} }{(2n)!}$ You get the choice of either the summation or just the expansion

Use the first two non-zero term (this phrase will be on the exam) to estimate $\sin (1.5)$ and compare with calculator.

$T _f ^{2}\left( 1.5;\ \frac{\pi}{2} \right) = 1 - \frac{\left( x-\frac{\pi}{2} \right) ^{2}}{2!}$

$\sin (1.5) \approx T _f ^{2}\left( 1.5;\ \frac{\pi}{2} \right) = 1 - \frac{\left( 1.5 - \frac{\pi}{2} \right) ^{2}}{2!} \approx 0.99749394$

Calculator value is

$\sin (1.5) = 0.99749498$

Recall this limit: $\lim_{x \to 0} \frac{\sin x}{x} = L’ = \lim_{x \to 0} \frac{\cos x}{1} = L’ = \frac{1}{1} = 1$

$\sin x \approx x$ for $x$ near 0.

$\lim_{x \to \frac{\pi}{2}} \frac{\sin \left( x- \frac{\pi}{2} \right) }{x- \frac{\pi}{2}} = 1$

$\sin x \approx x a- \frac{x^{3}}{3!} + \frac{x^5}{5!}$

The nth order Taylor Series at $a$ of $f(x)$ should approximate $f(x)$ very well when $x$ is is close to $a$ and when $n$ is big.

Example:

$f(x) = e^x$ centered at $a=0$

$T _{f} (x) = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!}$

$T _{f} ^1 (x) = 1+x$

$T _{f}^2 (x) = 1 + x + \frac{x^2}{2!}$

$T _{f}^3 (x) = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!}$

$T _{f} ^1 (2) = 1 + 2 = 3$

$T _{f} ^2 (2) = 1 + 2 + \frac{2^2}{2!}= 5$

$T _{f} ^3 (2) = 1 + 2 + 2 + \frac{8}{6} = 5 + \frac{4}{3} = 6.333…$

$T _{f} ^4 (2) = 7$

$f(2) = e^2 = 7.289$

Example:

$f(x) = \sqrt[3]{x}$ at $a=1$

$T _{f}^3 (x;\ 1) = c_0 + c_1 (x-1) + c_2(x-1)^2+c_3(x-1)^3$

$f’(x) = \frac{1}{3} x^{-\frac{2}{3}}$

$f’‘(x) = - \frac{2}{9} x^{-\frac{5}{3}}$

$f’’‘(x) = \frac{10}{27} x^{-\frac{8}{3}}$

$c_0 = \frac{f(1)}{0!} = \frac{\sqrt[3]{1}}{0!} = 1$

$c_1 = \frac{f’(1)}{1!} = \frac{1}{3} \frac{1}{1!} = \frac{1}{3}$

$c_2 = \frac{f’‘(1)}{2!} = -\frac{1}{9}$

$c_3 = \frac{f’’‘(1)}{3!} = \frac{5}{81}$

$T _{f}^{3} (x;\ 1) = 1 + \frac{1}{3}(x-1) - \frac{1}{9}(x-1)^2 + \frac{5}{81}(x-1)^3$

$T _{f}^{3} (1.2,\ 3) = 1 + \frac{0.2}{3} = 1.0666…$

$\sqrt[3]{1.2} = 1.06265$

Example:

$f(x) = \ln x$ at $a=1$

$c_0 = \frac{f(0)}{0!}$

$T _{f}^2 (x;\ 1) = c_0 + c_1(x-1) + c_2(x-1)$

$f(x) = \ln x$

$f’(x) = \frac{1}{x}$

$f’‘(x) = -\frac{1}{x^2}$

$c_0 = \frac{f(1)}{0!} = \frac{\ln 1}{0!} = 0$

$c_1 = \frac{f’(1)}{1!} = 1$

$c_2 = \frac{f’‘(1)}{2!} = -\frac{1}{2}$

$T _{f}^2 (x;\ 1) = (x-1) - \frac{(x-2)}{2}$

$T _{f}^2 (0.9;\ 1) = -0.1 - 0.05 = -0.15$

$T _{f}^2 (0.9) = (0.9 - 1) - \frac{(0.9 - 1)^2}{2} = -0.105$

Find the error:

$E = \mid \ln (0.9) - T _{f}^{2}(0.9;\ 1) \mid$

$E = \mid -0.10536 - (-0.105) \mid = \mid -0.00036 \mid = 0.00036$

Definitions

Here we establish the upper bound on the error in approximating a function by its Taylor Series. The so called Taylor-Lagerange Theorem. Without proof, the formula that gives $n$-th order error in Lagrange Theorem is:

It looks similar to the $n+1$ th order term in the Taylor Series with small exception that there is $C$ (unknown) instead of center of expansion $a$. Our goal is always to place an upper bound of $f^{(a+1)}(c)$ which does not have a $C$ in it, so this mysterious $C$ should be determined. and we will see that it will not constitute any problem to find this $C$. It will always be a number between $a$ and $x$.

Example:

$f(x) = e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!}$

We found that

$T _{f}^1 (0.1) = 1.1$

$T _{f}^3 (0.1) = 1.105166$

And the calculator value was $e^{0.1} = 1.1051709$

Question is: Can we use Lagrange formula for error to obtain upper bound on the error if we approximate $e^{0.1}$ by the 1st and 3rd order Taylor Series.

$E _{f}^n (0.1) = \mid \frac{f^{(n+1)}(c)}{(n+1)!} (0.1) ^{n+1} \mid = \frac{(0.1)^{n+1}}{(n+1)} \mid f^{n+1}(c) \mid$

$f(x) = e^x$

$f^{(n)}(x) = e^x \implies f^{(n+1)}(x) = e^x$ so $f^{(n+1)}(c) = e^c = \frac{(0.1)^{n+1}}{(n+1)!} e^{0.1}$

$[a;\ x]$

$[0,\ 0.1]$

$0\le c \le 0.1$

Recall:

$E _{f}^n (x;\ a) = \mid \frac{f^{(n+1)}(c)}{(n+1)!}(x-a)^{n+1} \mid$

$e^{x} = 1 + x + \frac{x^2}{2!}$

$T _{f}^1 (x) = 1 + x \implies T _{f}^1 (0.1) = 1 + 0.1 = 1.1$

$T _{f}^3 (x) = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} \implies T _{f}^3 (0.1) = 1.1051666$

Calculator value of $e^{0.1} = 1.10517091808$

Approximate $e^{0.1}$ by setting an upper bound error using Lagrange formula.

The error in approximation ($n$ order) is:

$E _{f} ^n (0.1) = \mid \frac{f^{(n+1)}(c)}{(n+1)!} (0.1)^{n+1} \mid = \frac{(0.1)^{n+1}}{(n+1)!} \mid f^{(n+1)}(c) \mid = \frac{\left( 0.1 \right) ^{n+1}}{(n+1)!}e^{c}$

$f(x) = e^x$

$f^{(n+1)}(x) = e^x \implies f^{(n+1)} (c) = e^{c}$

$c$ is between $[a;\ x]$, in our case $a=0$, $x=0.1$, therefore $e$ $c$ between $[0;\ 0.1]$. Since $e^{c} \le e^{0.1}$, then:

$E _{f}^{n}(0.1) \le \frac{(0.1)^{n+1}e^{0.1}}{(n+1)!}$

What should be the $n$ so that we would have 0.0001 error?

$E _{f}^1 (0.1) = \mid e^{0.1} - T _{f}^1 (0.1) \mid = 1.105… - 1.1 \mid = 0.00517$

$E _{f}^3 (0.1) = \mid e^{0.1} - T _{f}^{3} (0.1) \mid = 0.00000425808$ This is the actual error.

Now we want to get the upper bound error if we use 3 terms.

$E _{f}^3 (0.1) = \frac{(0.1)^{3+1}e^{0.1}}{(3+1)!} = \frac{0.0001 e^{0.1}}{24} = 0.0000046 \approx 0.5 x 10^{-6}$

On the quiz, you will be asked something like “how many terms do you need to get an error of 0.001 (or $10^{-3}$?”

To do this, you just need to check via trial-and-error

Example:

Find $n$ for an error of $\le 0.0001 = 10^{-4}$

$E _{f}^{1}(0.1) = \frac{(0.1)^{1+1}}{(1+1)!}e^{0.1} \approx 0.0055$

$E _{f}^{2}(0.1) = \frac{(0.1)^{2+1)}}{(2+1)!}e^{0.1} \approx 0.00018$

$E _{f}^{3}(0.1) = \frac{(0.1)^(3+1)}{(3+1)!} e^{0.1} \approx 0.0000046$

---

Question 1

• Evaluate 3rd order
• Taylor Expansion

Question 2

• Find $n+1$ derivative

Question 2b

• Use the result in a and find third order Taylor Series expansion centered at $a$.
• Find the error. Find 10 digits

Question 2c

• Use your answer from a and find the upper bound error in approximating your function

Question 2d

• Find the smallest $n$ such that the error is smaller or equal to a given value

---

Example:

$f(x) = \ln x$

• For $f(x) = \ln x$, find $f^{(n+1)}(x)$ derivative

$f’(x) = \frac{1}{x}$

$f’‘(x) = -\frac{1}{x^2}$

$f’’‘(x) = \frac{2}{x^3}$

$f^{(4) }(x) = -\frac{1(2)(3)}{x^4}$

$f^{(5)}(x) = \frac{1(2)(3)(4)}{x^5}$

$\therefore f^{(n)}(x) = \frac{(-1)^{n+1}(n-1)!}{x^n} \forall n\ge 1$

$f^{(n+1)}(x) = \frac{(-1)^{n}(n)!}{x^{n+1}}$

• Use the result in a to find $T _{f}^{3}(x;\ 1)$. That is, the 3rd order Taylor Series expansion centered at $a=1$. Then evaluate the error $E _{f}^3 (x;\ 1) = \mid f(x) - T _{f}^{2}(x;\ 1) \mid$ for $x = 1.1$

$T _{f}^3 (x;\ 1) = c_0 + c_1 (x-1) + c_2 (x-1)^2 + c_3(x-1)^3$

$c_0 = \frac{f(1)}{0!} = \frac{\ln 1}{0!} = 0$

$c_1 = \frac{f’(1)}{1!} = \frac{1}{1!} = 1$

$c_2 = \frac{f’‘(1)}{2!} = \frac{-1}{2!} = -\frac{1}{2}$

$c_3 = \frac{f’’‘(1)}{3!} = \frac{2}{3!} = \frac{1}{3}$

$T _{f}^3 (x;\ 1) = (x-1) - \frac{(x-1)^2}{2} + \frac{(x-1)^3}{3}$

• Find the error at $a=1.1$.

$E _{f}^3 (1.1;\ 1) = \mid \ln (1.1) - T _{f}^3(1.1;\ 1) \mid$

$E _{f}^3(1.1;\ 1) = \mid 0.0953101798 - \left(0.1 - \frac{(0.1)^2}{2} + \frac{(0.1)^3}{3} \right) \mid$

$= \mid -0.00002315353 \mid = 0.000023153$

• Use the result in part a to find the upper bound for the error $E _{f}^3 (x;\ 1)$ in approximating $f(x) = \ln x$ by $T _{f}^ 3 (x;\ 1)$ if $\mid x-1 \mid \le 0.1$

$E _{f}^3 (x;\ 1) = \mid \frac{f^{(n+1)}(c)}{(n+1)!}(x-1)^{x+1} \mid = \mid \frac{(-1)^{n+2}}{(n+1)!} \frac{n!}{C^{n+1}} (x-1)^{n+1} \mid = \frac{1}{n+1} \frac{1}{C^{n+1}} \mid x-1 \mid ^{n+1}$

$= \frac{1}{(n+1)C^{n+1}} (0.1)^{n+1}$

$\mid x - 1 \mid \le 0.1$

$0.9 \le x \le 1.1$

$0.9 \le C \le 1.1$

Because we are getting the upper bound, we want the smallest value of $C$ (which is 0.9).

$C=0.9$

$E _{f}^n (x;\ 1) \le \frac{1}{(n+1)(0.9)^{n+1}} = \frac{1}{n+1}\left( \frac{1}{9} \right) ^{n+1}$

$E _{f}^3 (x;\ 1) = \frac{1}{4}\left( \frac{1}{9} \right) ^{4} \approx 0.000038103$

• If $\mid x-1 \mid \le 0.1$, find the smallest $n$ so that this error will be less than or equal to 0.0001.

We already know that if $n=3$, the error is 0.000038103 and it is less than 0.0001. We should go on and check what if $n=2$ will give us again an error less than 0.0001.

Let $n=2$.

$E _{f}^2 (1.1;\ 1) = \frac{1}{2+1}\left( \frac{1}{9} \right) ^{2+1} = \frac{1}{3} \left( \frac{1}{9} \right) ^3 = \left( \frac{1}{3} \right)^{7} = 0.00045724$

No! Since 0.00045724 > 0.0001, then $n=3$ is the order that we must retain.

Example:

$f(x) = e^{3x}$

Part a:

$f’(x) = 3e^{3x}$

$f’‘(x) = 3^{2} e^{3x}$

$f’’‘(x) = 3^{3}e^{3x}$

$f^{(n)}(x) = 3^{n} e^{3x}$

Therefore, $f^{(n+1)}(x)=3^{n+1}e^{3x}$

$T _{f}^{3}(x;\ 0) = c_0 + c_1x + c_2 x^{2} + c_3 x^{3}$

$c_0 = \frac{f(0)}{0!} = \frac{e^{3(0)}}{0!} = \frac{1}{0!} = 1$

$c_1 = \frac{f’(0)}{1!} = \frac{3e^{0}}{1!} = \frac{3}{1!} = 3$

$c_2 = \frac{f’‘(0)}{2!} = \frac{9e^{0}}{2!} = \frac{9}{2}$

$c_3 = \frac{f’’‘(0)}{2!} = \frac{27e^{0}}{3!} = \frac{9}{2}$

$c_4 = \frac{81}{4!} = \frac{81}{24} = \frac{27}{8}$

Part b:

$T _f ^{3} (x) = 1 + 3x + \frac{9}{2}x^2 + \frac{9}{2}x^3$

$E _{f}^{3} (0.1) = \mid f(0.1) - T _{f}^{3}(0.1) \mid$

$= \mid e^{0.3} - \left( 1 + 0.3 + \frac{9}{2}(0.1)^{2} + \frac{9}{2}(0.1)^3 \right) \mid = 0.0003588$

Part c: Find upper bound for the error $E _{f}^{2}(x;\ 0)$ in approximating $f(x) = e^{3x}$ by $T _{f}^{3}(x;\ 0)$ if $\mid x \mid \le 0.1$

$E _{f}^{n} = \mid \frac{f^{(n+1)}(c)}{(n+1)!} x^{n+1} \mid$

$= \frac{3^{n+1}e^{3c}}{(n+1)!} \mid x \mid ^{n+1}$

$E _{f}^{3}(x;\ 0) = \frac{3^{4}e^{3c}}{4!} \mid x \mid ^{4} \le \frac{3^{4}e^{3c}}{4!} (0.1)^4$

$c = [0,\ 0.1]$

$e^{0} < e^{3(0.1)}$

$E _{f}^{3}(x;\ 0) = \frac{3^{4}e^{3c}}{4!} \mid x \mid ^{4} \le \frac{3^{4}e^{3c}}{4!} (0.1)^4 \le \frac{3^{4}e^{0.3}}{4!}(0.1)^4$

$E _{f}^{3} (x;\ 0) = \frac{3^{4}e^{3(c)}}{4!} \mid x \mid ^4 \le 0.0004555$

If $\mid x \mid \le 0.1$ find the smallest $n$ so that the error is less than 0.0001.

Since for $n=3$, $E _{f}^{2} = 0.0004555$ we try $n=4$

$E _{f}^{4}(0.1) = \frac{3^{5}e^{0.3}}{5!}(0.1)^5 = 0.00002732$

Example:

**Part a: For $f(x) = \ln (1+x)$, find $f^{(n+1)}(x)$ **

$f’(x) = \frac{1}{1+x}$

$f’‘(x) = \frac{-1}{(1+x)^2}$

$f’’‘(x) = \frac{2}{(1+x)^3}$

$f^{(n+1)}(x) = (-1)^{n} \frac{n!}{(1+x)^{n+1}}$

Part b: Use the answer from part A to find $T _{f}^{3}(x;\ 0)$. That is, Taylor Series at $a=0$. Also find $E _{f}^{3}(x;\ 0) = \mid f(x) - T _{f}^{3}(x;\ 0) \mid$ at $x=0.1$.

$T _{f}^{3}(x) = c_0 + c_1 x + c_2 x^{2} + c_3 x^{3}$

$c_n = \frac{f^{n}(0)}{n!}$

$c_0 = \frac{f(0)}{0!} = 0$

$c_1 = \frac{f’(0)}{1!} = 1$

$c_2 = \frac{f’‘(0)}{2!} = -\frac{1}{2}$

$c_3 = \frac{f’’‘(0)}{3!} = \frac{1}{3}$

$\therefore T _{f}^{3} (x;\ 0) = x - \frac{x^2}{2} + \frac{x^3}{3}$

$E _{f}^{3}(0.1) = \mid f(0.1) - T _{f}^{3}(0.1) \mid$

$= \mid \ln 1.1 - (0.1 - \frac{0.1^{2}}{2} + \frac{0.1^{3}}{3}) \mid = 0.00002315$ Part c: use $f^{(n+1)}(x)$ obtained in Part A to find $E _{f}^{3}(x;\ 0)$ if $\mid x \mid \le 0.1$

$f^{(n+1)}(c) = \frac{(-1)^{n}n!}{(1+c)^{n+1}}$

So $E _{f}^{n}(x) = \mid \frac{f^{(n+1)}(c)}{(n+1)!} x^{n+1} \mid$

$= \frac{n!}{(1+c)^{n+1}(n+1)!} \mid x \mid ^{n+1} = \frac{1}{(1+c)^{n+1}(n+1)} \mid x \mid ^{n+1}$

$E _{f}^{n}(0.1) = \frac{1}{(1+c)^{n+1}(n+1)}(0.1)^{n+1}$

$E _{f}^{3}(0.1) = \frac{1}{(1+c)^{3+1}(3+1)}(0.1)^{3+1}$

$-0.1 \le c \le 0.1$

Since we want the largest number, we choose $c=-0.1$.

$E _{f}^{3}(0.1) = \frac{1}{(1-0.1)^{3+1}(3+1)}(0.1)^{3+1} = 0.0000381039$

Part d: If $\mid x \mid \le 0.1$ find the smallest $n$ such that $E _{f}^{n}(0.1,\ 0)$ is less than $0.0001$.

Since the error for $n=3$ is 0.0000381 and it is smaller than the 0.0001, the answer is at most $n=3$. We now begin by checking $n$’s less than 3.

$E _{f}^{2}(0.1) = \frac{1}{3} \frac{1}{0.9^3}(0.1)^{3} = \frac{1}{3} \left( \frac{1}{9} \right) ^{3} = 0.00045725$

Since $E _{f}^{2}(0.1)$ is greater than 0.0001, then $n=3$ is the smallest.

Sequences and Series

We can expand our function into a Taylor Series. The main question is: for what values of $x$ this series is equal to the original function.

$e^{x} = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!}$

The answer based on the issue of convergence of the series. If it diverges, then there is no equality, otherwise the issue never narrows down to the issue of the interval of convergence.

Example:

$\frac{1}{1-x} = c_0 + c_1 x + c_2 x^2 + c_3 x^3 + c_4 x^4$

$\frac{1}{1-x} = 1+x+x^2+x^3+x^4 + …(-1,\ 1)$

$\frac{1}{1-x} = \sum_{n=0}^{\infty} \frac{x^{n}}{n}$

This means that this series is only exactly equal to $\frac{1}{1+x}$ for values between -1 and 1.

For example:

$x=0.2$

$\frac{1}{1-0.2} = 1.25$

$1 + 0.2 + 0.04 + … \approx 1.24$

What about $x=1.1$?

$\frac{1}{1-1.1} = -10$

$1 + 1.1 + … \approx 2.2$ not even close

What about $x=-0.2$?

$\frac{1}{1-(-0.2)} = \frac{1}{1.2} = 0.833$

$1-0.2 + 0.04 - 0.008 + … \approx 0.832$

Sequences

$\sum_{n=1}^{\infty} \frac{1}{n^2} = 1 + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} = \frac{\pi^{2}}{6}$

$\sum_{n=1}^{\infty} \ln (1+x) = x - \frac{x^2}{2} + \frac{x^3}{3} - \frac{x^4}{4} + … (-1,\ 1]$

A harmonic series is defined by $\sum_{n=1}^{\infty} \frac{1}{n} = 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + …$ and it is always divergent.

Alternating harmonic series: $\sum_{n=1}^{\infty} \frac{(-1)^{n+1}}{n} = \ln 2 = 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \frac{1}{5} - \frac{1}{6} + …$

• This converges

Example sequences:

$a_n = \frac{n}{n+1} = \frac{1}{2},\ \frac{2}{3},\ \frac{3}{4},\ \frac{4}{5}, …, \frac{n}{n+1},\ \frac{n+1}{n+2}$

$a_n = \frac{(-1)^{n}(n+1)}{3^{n}} = -\frac{2}{3},\ \frac{3}{9},\ -\frac{4}{27},\ \frac{5}{81}$

$1,\ 1,\ 2,\ 3,\ 5,\ 8,\ 13,\ 21,\ …$

$\frac{3}{5},\ -\frac{4}{25},\ \frac{5}{125},\ -\frac{6}{625},\ …$

$a_n = \frac{(-1)^{n}(n+2)}{5^{n}}$

$a_n = \frac{n^2}{n+1}$

$\lim_{n \to \infty} \frac{n^2}{n+1} = \infty$ so it diverges

Example series:

Consider the sequence: $1,\ \frac{1}{2},\ \frac{1}{3},\ \frac{1}{4} = a_n = \frac{1}{n}$

The series: $\sum_{n=1}^{\infty} a_n = \sum_{n=1}^{\infty} \frac{1}{n} = 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4}$

$1+2+3+4+5+…+n$, if we start to add, we get cumulative sum: $1,\ 3,\ 6,\ 10,\ 15,\ 21 = \frac{n(n+1)}{2}$

$\sum_{n=1}^{\infty} i = \frac{n(n+1)}{2}$

Example:

$\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + … + \frac{1}{2^{n}}$

What is the partial sum at each place?

$\frac{1}{2},\ \frac{3}{4},\ \frac{7}{8},\ \frac{15}{16}, …, \frac{63}{64}, …, 1 - \frac{1}{2^{n}}$

If the limit of this new sequence converges, then the original series converges

$\lim_{n \to \infty} 1 - \frac{1}{2^{n}} = 1$ (And the original series converges at 1)

Sum of Geometric Series

A geometric series is of form: $a + ar + ar^{2} + ar^{3} + … + ar^{n} = \sum_{n=0}^{\infty} ar ^{n} = \sum_{n=1}^{\infty} a r^{n-1}$

If $r=1$, then we get $a + a + a + … + a = \pm \infty$ if $n$ goes to $\infty$ and it diverges.

If $r \neq 1$, then $S_n = a + ar + ar^{2} + … + ar ^{n-1}$

$r S_n = ar + ar ^{2} + ar ^{3} + … + a r^{n-1} + ar^{n}$

$S_n - r S_n = a - a r^{n}$

$S_n (1-r) = a \left( 1-r^{n} \right) $

$S_n = \frac{a\left( 1-r^{n} \right) }{1-r} = \frac{1}{1-r} - \frac{ar^{n}}{1-r}$

$\lim_{n \to \infty} S_n = \lim_{n \to \infty} \left( \frac{a}{1-r} - \frac{a}{1-r}r^{n} \right)$

Recall that $\frac{a}{1-r}$ is a constant (and a limit of a constant is just a constant).

Cases:

• $-1 < r < 1$ (i.e. $\mid r \mid <1$)

$\lim_{n \to \infty} r^{n} = 0$

So $S_n = \frac{1}{1-r} = S$

• If $r>1$ or $r\le -1$

$\lim_{n \to \infty} r^{n} = \infty$ if $\mid r \mid > 1$ and also diverges if $r=-1$.

Thus, we generalize:

If $\mid r \mid < 1$, then Geometric Series $\sum_{n=0}^{\infty} a r ^{n}$ converges and, most importantly, equals $\frac{a}{1-r}$

NOTE: If asked on the final to find the sum of the series, it will be a geometric series

If $ \mid r \mid \ge 1$, then the Geometric Series diverges!

Example:

Find the sum of the Geometric Series: $5- \frac{10}{3} + \frac{20}{9} - \frac{40}{27} + …$

$= 5 \left( 1 - \frac{2}{3} + \frac{4}{9} - \frac{8}{27} + … \right)$

$r= -\frac{2}{3}$

$= 5 \sum_{n=0}^{\infty} \left( -\frac{2}{3} \right) ^{n}$

Therefore the sum is $5 \frac{1}{1-\left( -\frac{2}{3} \right)} = 5 \frac{1}{1+\frac{2}{3}} = 3$

Example:

$\sum_{n=1}^{\infty} 2^{2n} 3^{1-n} = \sum_{n=1}^{\infty} 4^{n} (3) 3^{-n} = 3 \sum_{n=1}^{\infty} \left( \frac{4}{3} \right) ^{n}$

$3 \sum_{n=1}^{\infty} \left( \frac{4}{3} \right) ^{n}$ is not in the form in a geometric series. Either you have to convert it to $\sum_{n=1}^{\infty} S^{n-1}$ or $\sum_{n=0}^{\infty} S^{n}$.

$3 \sum_{n=1}^{\infty} \left( \frac{4}{3} \right)^{n} \left( \frac{4}{3} \right)^{-1} \left( \frac{4}{3} \right)^{1} = 4 \sum_{n=1}^{\infty} \left( \frac{4}{3} \right)^{n-1}$

This diverges! (Because $\frac{4}{3}$ is greater than 1)

Example:

$\sum_{n=1}^{\infty} \frac{\left( -6 \right) ^{n-1}}{5^{n-1}} = \sum_{n=1}^{\infty} \left( -\frac{6}{5} \right) ^{n-1}$, since $r = \mid -\frac{6}{5} \mid >1$, the series diverges!

Example:

$\sum_{n=1}^{\infty} \frac{(-3)^{n-1}}{4^{n}} = \sum_{n=1}^{\infty} \frac{(-3)^{n-1}}{4^{n-1}(4)} = \frac{1}{4} \sum_{n=1}^{\infty} \left( -\frac{3}{4} \right) ^{n-1}$

So $r= -\frac{3}{4}$ and $\mid -\frac{3}{4} \mid <1$ converge!

$= \frac{1}{4} \frac{1}{1-\left( -\frac{3}{4} \right)} = \frac{1}{4} \frac{1}{1+\frac{3}{4}} = \frac{1}{7}$

Example:

$\sum_{n=1}^{\infty} \frac{e^{n}}{3^{n-1}} = \sum_{n=1}^{\infty} \frac{e^{n-1} e}{2^{n-1}} = e \sum_{n=1}^{\infty} \left( \frac{e}{3} \right)^{n-1}$

$\frac{e}{3} < 1$ so this converges!

$e \frac{1}{1-\frac{e}{3}} = \frac{3e}{3-e}$

Example:

Find the sum of the series $\sum_{n=0}^{\infty} x^{n}$ where $\mid x \mid < 1$:

$\sum_{n=0}^{\infty} x^{n} = 1 + x + x^2 + x^3 + … + x^n = \frac{1}{1-x}$

Proof via Taylor Series:

$\frac{1}{1-x} = f(x)$ into a Taylor Series:

$\frac{1}{1-x} = c_0 + c_1 x + c_2 x^2 + c_3 x^3 + … + c_n x^n$

$c_0 = c_1 = c_2 = … = c_n = 1$

$c_n = \frac{f^{(n)}(0)}{n!} = 1 + x + x^2 + x^3 + … + x^n$

This converges for all values $-1 < x < 1$

Telescoping Series

$\sum_{n=1}^{\infty} \frac{1}{n(n+1)}$

$S_n = \sum_{i=1}^{n} \frac{1}{i(i+1)} = \frac{1}{1(2)} + \frac{1}{2(3)} + \frac{1}{3(4)} + \frac{1}{(n-1)(n)} + \frac{1}{n(n+1)}$

$\frac{1}{i(i+1)} = \frac{1}{i} - \frac{1}{i+1}$

$S_n = \sum_{n=1}^{\infty} \left( \frac{1}{i} - \frac{1}{i+1} \right) = \left( 1-\frac{1}{2} \right) + \left( \frac{1}{2} - \frac{1}{3} \right) + \left( \frac{1}{3} - \frac{1}{4} \right) + … + \left( \frac{1}{n-1} - \frac{1}{n} \right) + \left( \frac{1}{n} - \frac{1}{n+1} \right)$

$S_n = 1 - \frac{1}{n+1}$

$\lim_{n \to \infty} S_n = \lim_{n \to \infty} 1 - \frac{1}{n+1} = 1$

Harmonic Series

$\sum_{n=1}^{\infty} \frac{1}{n} = 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + … + \frac{1}{n}$

$S_1 = 1$

$S_2 = 1 + \frac{1}{2}$

$S_4 = 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4}$

$= 1 + \frac{1}{2} + \left( \frac{1}{3} + \frac{1}{4} \right) + \left( \frac{1}{5} + \frac{1}{6} + \frac{1}{7} + \frac{1}{8} \right) + \left( \frac{1}{9} + \frac{1}{10} + \frac{1}{11} + … + \frac{1}{16} \right) < 1 + \frac{1}{2} + \left( \frac{1}{4} + \frac{1}{4} \right) + \left( \frac{1}{8} + \frac{1}{8} + … + \right) + …$

$= 1 + \frac{1}{2} + \frac{1}{2} + \frac{1}{2} + …$

$S_4 = 1 + \frac{2}{2}$

$S_8 = 1 + \frac{3}{2}$

$S_{16} = 1 + \frac{4}{2}$

$S_{32} = 1 + \frac{5}{2}$

$S_{64} = 1 + \frac{6}{2}$

$\lim _{n \to \infty} S _{2^{n}} = \lim _{n \to \infty} \left( 1+\frac{n}{2} \right) = \infty$ therefore it diverges. Thus, Harmonic Series diverges!

If the series $\sum_{n=1}^{\infty} a_{n}$ is convergent, then $\lim_{n \to \infty} a_{n} = 0$.

The converse is not true! That is, if $\lim_{n \to \infty} a_n = 0$, that does not mean that $\sum_{n=0}^{\infty} a_n$ is convergent. An example would be $\sum_{n=1}^{\infty} \frac{1}{n}$

Example:

$\sum_{n=0}^{\infty} \left( \frac{1}{2} \right) ^{n}$

This series converges because it is Geometric and $-1<r<1$

Divergence Test - Term Test

If $\lim_{n \to \infty} a_{n} \neq 0$ or does not exist, then series Diverges.

Example:

$\sum_{n=1}^{\infty} \frac{n^{2}}{5 n^{2} + 4}$

$\lim_{n \to \infty} \frac{n^{2}}{5n^{2} + 4} = \frac{1}{5}$ Therefore it diverges.

Example:

$\lim_{x \to \infty} \frac{3-2x}{x+15000} = -2$ therefore it diverges.

Example:

$\lim_{n \to \infty} \frac{n^{2}+9}{n^{3}-2n} = 0$ So it’s not conclusive.

Example:

$\sum_{n=1}^{\infty} \frac{2n}{3n+1}$

$\lim_{n \to \infty} \frac{2n}{3n+1} = \frac{2}{3}$ therefore it is divergent

Example:

Find the sum of the series $\sum_{n=1}^{\infty} \left( \frac{3}{n(n+1)} + \frac{1}{2^{n}} \right)$.

$= 3 \sum_{n=1}^{\infty} \frac{1}{n(n+1)} + \sum_{n=1}^{\infty} \frac{1}{2^{n}}$

$= 3 (1) + \sum_{n=1}^{\infty} \frac{1}{2^{n}}$

The second part isn’t quite a Geometric Series (because you start at 1 and it’s not of type $\sum_{n=1}^{\infty} a^{n-1}$).

Let $n=m+1$,

$= 3 (1) + \frac{1}{2} \sum_{m=0}^{\infty} \left( \frac{1}{2} \right) ^{m}$

Now, $m=n$:

$= 3 + \frac{1}{2} \sum_{n=0}^{\infty} \left( \frac{1}{2} \right) ^{n}$

Sum of Geometric Series:

$\frac{1}{2} \sum_{n=1}^{\infty} \left( \frac{1}{2} \right) ^{n} = \frac{1}{2} \frac{1}{1-\frac{1}{2}} = \frac{1}{2} (2) = 1$

$= 3 + 1 = 4$

Example:

$\sum_{n=4}^{\infty} \frac{1}{2^{n}}$

Example:

$\sum_{n=2}^{\infty} \left( \frac{3}{2} \right) ^{n}$

$\sum_{n=2}^{\infty} \left( \frac{3}{2} \right) ^{n} + \left( 1 + \frac{3}{2} \right) - \left( 1+\frac{3}{2} \right) = \sum_{n=0}^{\infty} \left( \frac{3}{2} \right) ^{n} - \left( 1 + \frac{3}{2} \right)$

Example:

$\sum_{n=4}^{\infty} \frac{n}{n^{3} + 1}$ is convergent, then:

$\sum_{n=1}^{\infty} \frac{n}{n^{3}+1} = \frac{1}{2} + \frac{2}{9} + \frac{3}{28} + \sum_{n=4}^{\infty} \frac{n}{n^{3}+1}$

Example:

$\sum_{j=0}^{\infty} \frac{7}{5^{j}} = 7 \sum_{j=0}^{\infty} \left( \frac{1}{5} \right) ^{j}$

$= 7 \frac{1}{1-\frac{1}{5}} = 7 \frac{5}{4} = \frac{35}{4}$

Example:

$\sum_{j=0}^{\infty} \left( -\frac{5}{7} \right) ^{j}$ This is a geometric series so:

$= \frac{1}{1-\left( -\frac{5}{7} \right) } = \frac{1}{1+\frac{5}{7}} = \frac{7}{12}$

Example:

$\sum_{k=1}^{\infty} \frac{5(-1)^k}{3^{k}} = 5 \sum_{k=1}^{\infty} \left( -\frac{1}{3} \right) ^{k} = 5 \sum_{k=1}^{\infty} \left( -\frac{1}{3} \right) ^{k-1} \left( -\frac{1}{3} \right)$

$= -\frac{5}{3} \sum_{k=1}^{\infty} \left( -\frac{1}{3} \right) ^{k-1}$

$\mid r \mid = \frac{1}{3} < 1$

$= -\frac{5}{3} \frac{1}{1-\left( -\frac{1}{3} \right) } = -\frac{5}{4}$

Example:

$\sum_{n=1}^{\infty} \frac{(-1)^{n}}{10n} = \frac{1}{10} \sum_{n=1}^{\infty} \frac{(-1)^{n}}{n} = \frac{1}{10} \left( -1 + \frac{1}{2} - \frac{1}{3} + \frac{1}{4} - \frac{1}{5} +… \right)$

Recall that $1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5} = \ln 2$

$= \frac{1}{10} \left( -\ln 2 \right) = \frac{-\ln 2}{10}$

Example:

$\sum_{n=0}^{\infty} \left( \frac{2}{7^{n}} + \frac{5(-1)^{n}}{3^{n}} \right) = 2 \sum_{n=0}^{\infty} \left( \frac{1}{7} \right) ^{n} + 5 \sum_{n=0}^{\infty} \left( -\frac{1}{3} \right) ^{n}$

$= 2 \frac{1}{1-\frac{1}{7}} + 5 \frac{1}{1-\left( -\frac{1}{3} \right) } = 2 \frac{7}{6} + 5 \frac{3}{4} = \frac{73}{12}$

Example:

$\sum_{n=0}^{\infty} \left( \frac{n}{7} + \frac{5(-1)^n}{3^{(n)}} \right)$ This diverges!

Example:

$\sum_{n=1}^{\infty} \left( \frac{n-1}{n} + \frac{3}{2^{n}} \right)$ The first part diverges and the second part converges therefore the entire sum diverges.

Integral Test

For $\sum_{n=m}^{\infty} a_n$ we say the series is convergent if and only if the improper integral $\int_{m}^{\infty} f(x) dx$ is convergent where $f(x) = a_n = f(n)$.

If $\int_{m}^{\infty} f(x) dx$ is divergent, then $\sum_{n=m}^{\infty} a_n$ is also divergent.

Example:

$\sum_{n=4}^{\infty} \frac{1}{(n-3)^{2}}$

$\int_{4}^{\infty} \frac{dx}{\left( x-3 \right) ^{3}} = \lim_{t \to \infty} \int_{4}^{t} \frac{dx}{\left( x-3 \right) ^{2}} = \lim_{t \to \infty} \left( -\frac{1}{(x-3)^{2}}\right) _4 ^t = 1$ Therefore it converges! But that doesn’t tell you what it converges to! In this example, the series converges to $\frac{\pi^{2}}{6}$

Example:

$\sum_{n=1}^{\infty} \frac{1}{n^{2}+1}$

$\int_{1}^{\infty} \frac{dx}{x^{2}+1} = \lim_{t \to \infty} \int_{1}^{t} \frac{dx}{x^{2}+1} = \lim_{t \to \infty} \tan ^{-1} x \mid _1 ^{t} = \frac{\pi}{4}$ Therefore the series converges.

Example:

$\sum_{n=1}^{\infty} \frac{1}{n}$

$\int _{1}^{\infty} \frac{dx}{x} = \lim _{t \to \infty} \ln x \mid _{1}^{t} = \lim _{t \to \infty} \ln t = \infty$ therefore the series diverges!

Example:

$\sum_{n=2}^{\infty} \frac{1}{n(\ln n)^{2}}$

$f(x) = \frac{1}{x \left( \ln x \right) ^{2}}$

$\int_{2}^{\infty} \frac{1}{x\left( \ln x \right) ^{2}}dx$

$= \lim_{t \to \infty} \left( -\frac{1}{\ln x} \right) _2 ^t = \frac{1}{\ln 2}$ Therefore the series converges

Example:

$\sum_{n=m}^{\infty} \frac{\ln n}{n}$

$\int_{m}^{\infty} \frac{\ln x}{x}dx$ Diverges

P-Series Test

Consider example $\sum_{n=1}^{\infty} \frac{1}{n^{p}}$. Does this converge or diverge?

If $p=1$, then it is a harmonic series and it diverges!

If $p < 0$, then $\lim_{n \to \infty} \frac{1}{n^{p}} = \infty$ and it diverges!

If $p = 0$, then $\lim_{n \to \infty} \frac{1}{n^{p}} = 1$ or if $\lim_{n \to \infty} \neq 0$ then the series diverges.

If $p > 0$, then we have $f(x) = \frac{1}{x^{p}}$. $\int_{1}^{\infty} \frac{dx}{x^{p}} = \frac{1}{p-1}$ if $p > 1$ and so it converges!

If $p < 1$, then it diverges.

To summarize:

$\int_{1}^{\infty} \frac{dx}{x^{p}}$ is convergent if $p>1$ and divergent if $p \le 1$.

Example:

$\sum_{n=1}^{\infty} \frac{1}{n^{3}}$

Since $p = 3 > 1$, the series converges

Example:

$\sum_{n=2}^{\infty} \frac{1}{n^{\frac{5}{3}}}$

$p = \frac{5}{3} > 1$ therefore it converges

Example:

$\sum_{n=1}^{\infty} \frac{1}{\sqrt{n} }$

$p = \frac{1}{2} < 1$ therefore divergent

Example:

$\sum_{n=1}^{\infty} \frac{1}{n^{3}}$ This converges because $p=3 > 1$.

Comparison Test

Suppose $\sum_{n=m}^{\infty} a_n$ and $\sum_{n=m}^{\infty} b_n$ are series with positive terms and that $a_n < b_n$. Then:

1. If $\sum_{n=m}^{\infty} b_n$ converges, then so does $\sum_{n=m}^{\infty} a_n$
2. If $\sum_{n=m}^{\infty} a_n$ diverges, then $\sum_{n=m}^{\infty} b_n$ also diverges.

Example:

$\sum_{n=1}^{\infty} \frac{n}{n^{3}+7}$

$\frac{n}{n^{3}+7} < \frac{n}{n^{3}} = \frac{1}{n^{2}}$

And we know that $\frac{1}{n^{2}}$ converges because $p = 2 > 1$.

Example:

$\sum_{n=1}^{\infty} \frac{1}{n^{2}+3}$

$\frac{1}{n^{2}+3} < \frac{1}{n^{2}}$

Since $\frac{1}{n^{2}}$ converges, (by $p=2 > 1$) $\sum_{n=1}^{\infty} \frac{1}{n^{2}+3}$ also converges.

Example:

$\sum_{n=1}^{\infty} \frac{1}{n - 0.5}$

$\frac{1}{n-0.5} > \frac{1}{n}$

Since $\frac{1}{n}$ diverges (Harmonic Series), $\sum_{n=1}^{\infty} \frac{1}{n-0.5}$ also diverges.

Limit Comparison Test

Suppose both $\sum_{n=1}^{\infty} a_n$ and $\sum_{n=1}^{\infty} b_n$ are series with positive terms, then if $\lim_{n \to \infty} \frac{a_{n}}{b_b} = L$ where $L\ge 0$ and is a finite number.

1. If $L \neq 0$ and $L \neq \infty$, then both series converge or both diverge. That is, they have the same behavior.
2. If $L = 0$ and $\sum_{n=m}^{\infty} b_n$ converges, them $\sum_{n=m}^{\infty} a_n$ also converges.
3. If $L = \infty$ and $\sum_{n=m}^{\infty} b_n$ diverges, then $\sum_{n=m}^{\infty} a_n$ also diverges.

Example:

$\sum_{n=0}^{\infty} \frac{1}{n^{2} - 0.2}$

$\frac{1}{n^{2} - 0.5} > \frac{1}{n^{2}}$

Since $\frac{1}{n^{2}}$ converges ($p=2>1$), we cannot say anything about $\frac{1}{n^{2}-0.5}$ using the comparison test.

$\lim_{n \to \infty} \frac{\frac{1}{n^{2}-0.5}}{\frac{1}{n^{2}}} = \lim_{n \to \infty} \frac{n^{2}}{n^{2}-0.5} = 1$

Because $\frac{1}{n^{2}}$ converges, $\frac{1}{n^{2}-0.5}$ also converges.

Example:

$\sum_{n=1}^{\infty} \frac{3n}{\sqrt{5+n^{5}}}$

$\frac{3n}{\sqrt{5 + n^{5}}} < \frac{3n}{\sqrt{n^{5}}} = \frac{3}{n^{\frac{3}{2}}}$

$\frac{3}{n^{\frac{3}{2}}}$ converges via the p-series test ($p = \frac{3}{2} > 1$)

By the comparison test, $\sum_{n=1}^{\infty} \frac{3n}{\sqrt{5+n^{5}}}$ converges.

Example:

$\sum_{n=1}^{\infty} \frac{2n^{2}}{\sqrt{5+n^5}}$

If we try to use the comparison test, it is not conclusive:

$\frac{2n^{2}}{\sqrt{5+n^5}} < \frac{2n^{2}}{\sqrt{n^{5}}} = \frac{2}{n^{\frac{1}{2}}}$

By the p-series test, $\frac{2}{n^{\frac{1}{2}}}$ diverges ($p = \frac{1}{2} < 1$).

We move to the limit comparison test.

$\lim_{n \to \infty} \frac{a_n}{b_n} = \lim_{n \to \infty} \frac{2n^{2}}{\sqrt{5+n^{5}}} \frac{\sqrt{n^{5}}}{2n^{2}} = \lim_{n \to \infty} \left( \frac{n^{5}}{5+n^{5}} \right)^{\frac{1}{2}} = 1$

We know that they have the same behavior so $\sum_{n=1}^{\infty} \frac{2n}{\sqrt{5+n^{5}}}$ diverges.

Ratio Test

Suppose $\sum_{n=1}^{\infty} b_n$ where $b_k \ge 0$ and that the $\lim_{n \to \infty} \frac{b_{k+1}}{b_k}$ exists as a real number $L$.

1. If $L < 1$, then the given series converges.
2. If $L > 1$, then the given series diverges.
3. If $L = 1$, then the test is not conclusive.

Example:

$\sum_{n=1}^{\infty} \frac{1}{n}$

$b_n = \frac{1}{n}$

$b_{n+1} = \frac{1}{n+1}$

$\lim_{n \to \infty} \frac{b_{n+1}}{b_n} = \lim_{n \to \infty} \frac{1}{n+1} \frac{n}{1} = 1$

Example:

$\sum_{k=1}^{\infty} \frac{k!}{5^{k}}$

$\lim_{k \to \infty} \frac{a_{k+1}}{a_k} = \lim_{k \to \infty} \frac{(k+1)!}{5^{k+1}} \frac{5^{k}}{k!} = \lim_{k \to \infty} \frac{1}{5} (k+1) = \infty$ So this series diverges!

Example:

$\sum_{k=1}^{\infty} \frac{k^{100}}{1.01^{k}}$

$\lim_{k \to \infty} \frac{(k+1)^{100}}{1.01^{k+1}} \frac{1.01^{k}}{k^{100}}$

$\lim_{k \to \infty} \frac{1}{1.01} \left( \frac{k+1}{k} \right) ^{100} = \frac{1}{1.01} < 1$

Therefore it converges.

Example:

$\sum_{k=1}^{\infty} \frac{4^{k}(k+1)}{k^{k}}$

$\lim_{k \to \infty} \frac{4^{k+1}(k+2)}{(k+1)^{k+1}} \frac{k^{k}}{4^{k}(k+1)}$

$= 4 \lim_{k \to \infty} \frac{k+2}{k+1} \frac{k^{k}}{(k+1)^{k+1}}$

$= 4 \lim_{k \to \infty} \left( \frac{k+2}{k+1} \right) \lim_{k \to \infty} \left( \frac{k}{k+1} \right)^{k} \lim_{k \to \infty} \frac{1}{k+1}$

Recall that $\lim_{x \to \infty} \left( 1 + \frac{1}{x} \right) ^{x} = e$

Which means that $\lim_{k \to \infty} \left( \frac{k}{k+1} \right)^{k} = \lim_{k \to \infty} \frac{1}{\left( 1+\frac{1}{k} \right) ^{k}} = \frac{1}{e}$

$= 4 (1) \left( \frac{1}{e} \right) (0) = 0$

Root Test

Consider series $\sum_{k=1}^{\infty} b_k$ where $b_k \ge 0$. Suppose that $\lim_{k \to \infty} \sqrt[k]{b_k}$ exists as a real number $L$.

1. If $L < 1$, the series converges
2. If $L > 1$ (including $\infty$), the series diverges
3. If $L = 1$, it is inconclusive

Example: $\sum_{k=1}^{\infty} \left( \frac{1}{2} + \frac{1}{k} \right) ^{k}$

$\lim_{k \to \infty} \sqrt[k]{\left( \frac{1}{2} + \frac{1}{k} \right)^{k}} = \lim_{k \to \infty} \left( \frac{1}{2} + \frac{1}{k} \right) = \frac{1}{2} < 1$ therefore the series converges.

Example:

$\sum_{n=1}^{\infty} \left( \frac{5n+3}{3n+5} \right) ^{n}$

$\lim_{n \to \infty} \sqrt[n]{ \left( \frac{5n+3}{3n+5} \right) ^{n}} = \lim_{n \to \infty} \frac{5n+3}{3n+5} = \frac{5}{3} > 1$ therefore the series diverges

---

Quiz tomorrow (50 minutes)

5 questions + bonus

1. a and b, does the series converge/diverge (find the sum if it converges)
2. a and b, Use the ratio test to determine if the following series converges or diverges
3. use the integral test to determine if the series converges or diverges
4. a and b, for the following two problems, determine if a series diverges or converges when using the test, name the test that you are using.
5. determine if the series converges or diverges by using (a) comparison test (b) limit comparison test
6. Bonus: for the series in the last question, use any other test to find if it converges or diverges.

---

Example:

$\sum_{n=1}^{\infty} \frac{1+\sqrt{n} }{n^{\frac{5}{4}}} = \sum_{n=1}^{\infty} \frac{1}{n^{\frac{5}{4}}} + \sum_{n=1}^{\infty} \frac{\sqrt{n} }{n^{\frac{5}{4}}}$

$= \sum_{n=1}^{\infty} \frac{1}{n^{\frac{5}{4}}} + \sum_{n=1}^{\infty} \frac{1}{m^{\frac{3}{4}}}$

First part converges, but the second one diverges so the original series diverges.

Example:

$\sum_{p=1}^{\infty} \frac{7 + p^{\frac{1}{7}}}{p^{\frac{8}{7}}}$

$= \sum_{p=1}^{\infty} \frac{7}{p^{\frac{8}{7}}} + \sum_{p=1}^{\infty} \frac{1}{p}$

First part converges, second part diverges so the series diverges.

Example:

$\sum_{k=2}^{\infty} \frac{5}{j (\ln j)^{2}}$

Use the integral test

$\int_{2}^{\infty} \frac{5dx}{x\left( \ln x \right) ^{2}} = \frac{5}{\ln 2}$ therefore the series converges

Example:

$\sum_{k=1}^{\infty} \frac{3k + 5}{k^{3}} = \sum_{k=1}^{\infty} \frac{3}{k^{2}} + \sum_{k=1}^{\infty} \frac{5}{k^{3}}$

Both parts converge, so the series converges.

Example:

$\sum_{k=1}^{\infty} \frac{3k^{3}+5}{k^{3}} = \sum_{k=1}^{\infty} 3 + \sum_{k=1}^{\infty} \frac{5}{k^{3}}$

First part diverges, second part converges so the entire series diverges.

Example (similar to quiz?):

$\sum_{k=1}^{\infty} \frac{1+\sin k}{k^{2}}$

The numerator can only be between 0 and 2.

$\frac{1+\sin k}{k^{2}} \le \frac{2}{k^{2}}$

$\frac{2}{k^{2}}$ is convergent which means that $\frac{1+\sin k}{k^{2}}$ also converges.

Example:

$\sum_{j=0}^{\infty} \frac{1}{2^{j} +1}$

$\frac{1}{2^{j} =1 } < \frac{1}{2^{j}} = \left( \frac{1}{2} \right)^{j}$

So this series converges

Example:

$\sum_{p=1}^{\infty} \frac{p+1}{0.9^p}$

$\frac{p+1}{0.9^p} > \frac{p+1}{1^{p}} = \frac{p+1}{1} = p+1$

Because $p+1$ is divergent, $\frac{p+1}{0.9^{p}}$ is also divergent.

You can also do:

$\frac{p+1}{0.9^{p}} > \frac{1}{0.9^{p}} = \left( \frac{1}{0.9} \right)^{p}$

$p = \frac{1}{0.9} > 1$ therefore it is divergent

Example:

$\sum_{m=1}^{\infty} \frac{4}{0.9^{m} + m^{2}}$

$\frac{1}{0.9^{m}+m^{2}} < \frac{1}{0.9^{m}}$

$\frac{1}{0.9^{m}}$ is divergent so this test is inconclusive.

Try comparing with a different series:

$\frac{1}{0.9^{m} + m^{2}} < \frac{1}{m^{2}}$

Because $\frac{1}{m^{2}}$ converges, the original series $\sum_{m=1}^{\infty} \frac{4}{0.9^{m} + m^{2}}$ also converges.

Example:

$\sum_{j=3}^{\infty} \frac{5}{j^{2} \ln j}$

$\frac{5}{j^{2}\ln j} < \frac{5}{j^{2}}$

So the series converges

Example:

$\sum_{k=1}^{\infty} \frac{k+5}{k^{2}}$

$\frac{k+5}{k^{2}} > \frac{k}{k^{2}} = \frac{1}{k}$

Since $\frac{1}{k}$ diverges, $\frac{k+5}{k^{2}}$ also diverges.

Example:

$\sum_{k=1}^{\infty} \frac{5k}{k! + 1}$

$\lim_{k \to \infty} \frac{5(k+1)}{(k+1)! + 1} \frac{k! + 1}{5k} = 0 < 1$

Therefore the series converges.

Alternating Series Test

An alternating series is a series whose terms are alternately positive and negative.

The following test says that if the alternating series decreases towards 0 in absolute value, then the series converges.

If the alternating series $\sum_{n=1}^{\infty} (-1)^{n-1} b_n = b_1 - b_2 + b_3 - b_4 + b_5 - b_6 + … (b_n > 0)$

If the series satisfies:

1. $b_{b+1} \le b_n$ for all $n$
2. $\lim_{n \to \infty} b_n = 0$ (if the limit does not exist, then the series diverges)

Then the series converges.

Example:

$1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \frac{1}{5} - \frac{1}{6} + … = \sum_{n=1}^{\infty} \frac{(-1)^{n-1}}{n}$ (Alternating harmonic series)

Converges conditionally. Example:

$-\frac{1}{2} + \frac{2}{3} - \frac{3}{4} + \frac{4}{5} - \frac{5}{6} + … = \sum_{n=1}^{\infty} (-1)^{n} \frac{n}{n+1}$

Example:

The alternating harmonic series $\sum_{n=1}^{\infty} \frac{(-1)^{n-1}}{n} = 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + …$

Satisfies:

1. $b_{n+1} \le b_n$ because $\frac{1}{n+1} < \frac{1}{n}$
2. $\lim_{n \to \infty} b_n = \lim_{n \to \infty} \frac{1}{n} = 0$

So by Alternating Series Test, the series converges.

Example:

$\sum_{n=1}^{\infty} \frac{(-1)^{n}3n}{4n-1} = -1 + \frac{6}{7} - \frac{9}{11} + \frac{12}{15} - …$

Conditions:

1. $b_{n+1} = \frac{(-1)^{n+1}3(n+1)}{4(n+1)-1} = \frac{3n+3}{4n+3} < \frac{3n}{4n-1}$ (passes)
2. $\lim_{n \to \infty} b_n = \frac{(-1)^{n}3n}{4n-1} = \frac{3}{4} \neq 0$ (fails)

Therefore by the Alternating Series Test, the series diverges.

Example:

$\lim_{n \to \infty} \frac{(-1)^{n}3n}{4n-1}$

$\lim_{n \to \infty} \frac{(-1)^{n}3n}{4n-1} = DNE$

Therefore, by the Divergence Test, the series diverges.

Example:

$\sum_{n=1}^{\infty} \frac{n^{3}}{\sqrt{n} -1}$

$\lim_{n \to \infty} \frac{n^{3}}{\sqrt{n} -1} = \infty \neq 0$

Therefore, by the Divergence Test, the series diverges.

Example:

$\sum_{n=1}^{\infty} \frac{(-1)^{n-1}}{n}$

$\lim_{n \to \infty} \frac{(-1)^{n-1}}{n} = \frac{\lim_{n \to \infty} (-1)^{n-1}}{\lim_{n \to \infty} n} = \frac{\text{Finite Number}}{\infty} = 0$

Therefore the Divergence Test is inconclusive.

Example:

$\sum_{n=1}^{\infty} (-1)^{n+1} \frac{n^{2}}{n^{3} + 1}$

The $\lim_{n \to \infty} (-1)^{n+1} \frac{n^{2}}{n^{3}+1}= 0$ so the divergence test is inconclusive.

Conditions of alternating series test:

• $b_{n+1} = \frac{(n+1)^{2}}{(n+1)^{3} + 1} < b_{n} = \frac{n^{2}}{n^{3} + 1}$ (passes)
• $\lim_{n \to \infty} \frac{n^{2}}{n^{3}+1} = 0$ (passes)

Therefore, by the Alternating Series Test, the series converges.

Example:

$\sum_{n=1}^{\infty} (-1)^{n-1} \frac{1}{n^{2}} = 1 - \frac{1}{2^{2}} + \frac{1}{3^2} - \frac{1}{4^2}$

$\sum_{n=1}^{\infty} \mid b_k \mid = \sum_{n=1}^{\infty} \frac{1}{n^{2}}$ converges so the original series converges absolutely.

Absolute Convergence

Suppose $\sum_{n=1}^{\infty} b_k$ is an Alternating Series, then the corollary (proposition) tells that the convergence of $\sum_{n=1}^{\infty} \mid b_k \mid$ implies the convergence of $\sum_{n=1}^{\infty} b_k.$ Namely, if $\sum_{n=1}^{\infty} \mid b_k \mid$ converges, then $\sum_{n=1}^{\infty} b_k$ converges.

For this type of convergence of $\sum_{n=1}^{\infty} b_k$ there is a special name.

Power Series and Radius of Convergence

Example:

$f(x) = x^{2} \cos (x^{2}) = c_0 + c_1 x + c_2 x^{2} + c_3 x^{3} + …$

Given $\cos x = 1 - \frac{x^{2}}{2!} + \frac{x^{4}}{4!} - \frac{x^{6}}{6!} + …$

$f(x) = x^{2} \left( 1 - \frac{x^{4}}{2!} + \frac{x^{8}}{4!} - \frac{x^{12}}{61} + … \right) = x^{2} + \frac{x^{10}}{4!} - \frac{x^{14}]}{6!} + …$

Example:

$e^{-x} = 1 - \frac{x}{1!} + \frac{x^{2}}{2!} - \frac{x^3}{3!} + \frac{x^4}{4!} - \frac{x^5}{5!}$

Example:

For what values of $x$ is the series $\sum_{n=0}^{\infty} n! x^{n}$ converge?

$\lim_{n \to \infty} \mid \frac{a_{n+1}}{a_n} \mid = \lim_{n \to \infty} \mid \frac{(n+1)! x^{n+1}}{n! x^{n}} \mid = \lim_{n \to \infty} (n+1) \mid x \mid = \infty$ if $x\neq 0$.

Thus, the given series converges only if $x=0$.

Example:

For what values of $x$ does the series $\sum_{n=1}^{\infty} \frac{(x-3)^{n}}{n}$ converge?

$\lim_{n \to \infty} \mid \frac{a_{n+1}}{a_n} \mid = \lim_{n \to \infty} \mid \frac{(x-3)^{n+1}}{n+1} \frac{n}{(x-3)^{n}} \mid$

$= \lim_{n \to \infty} \frac{n}{n+1} \mid x - 3 \mid = \mid x-3 \mid \lim_{n \to \infty} \frac{n}{n+1} = \mid x-3 \mid$

By the ratio test, the series converges if $\mid x-3 \mid <1$.

$-1 < x-3 < 1$

$2 < x < 4$

Check end points (which are $x=2$ and $x=4$).

$x=2$: $\sum_{n=1}^{\infty} \frac{(-1)^{n}}{n}$ this is the Alternating Harmonic Series (which is convergent) so $x=2$ is included

$x=4$: $\sum_{n=1}^{\infty} \frac{1}{n}$ this is the Harmonic Series, therefore it diverges so $x=4$ is not included.

Therefore, the interval of convergence is $[2,\ 4)$.

Example:

$\sum_{n=0}^{\infty} \frac{(-3)^{n}x^{n}}{\sqrt{n+1}}$

$\lim_{n \to \infty} \mid \frac{a_{n+1}}{a_n} \mid = \lim_{n \to \infty} \mid \frac{(-3)^{n+1}x^{n+1}}{\sqrt{n+2}} \frac{\sqrt{n+1}}{(-3)^{n}x^{n}} \mid = 3 \mid x \mid \lim_{n \to \infty} \sqrt{\frac{n+1}{n+2}} = 3 \mid x \mid$

$\mid x \mid < \frac{1}{3}$ therefore $R = \frac{1}{3}$.

Check end points (which are $x=-\frac{1}{3}$ and $x=\frac{1}{3}$ )

If $x=-\frac{1}{3}$, then $\sum_{n=1}^{\infty} \frac{(-3)^{n} (-3)^{-n}}{\sqrt{n+1}} = \sum_{n=1}^{\infty} \frac{1}{\sqrt{n+1}}$

Compare that with $\sum_{n=1}^{\infty} \frac{1}{n^{\frac{1}{2}}}$ and by the P-Series test, it diverges.

If $x=\frac{1}{3}$

$\sum_{n=1}^{\infty} \frac{(-3)^n \left( \frac{1}{2} \right)^{n}}{\sqrt{n+1}} = \sum_{n=1}^{\infty} \frac{(-1)^{n}}{\sqrt{n+1}}$

Alternating series test so we use Alternating Series Test

1. $b_{n+1} < b_{n} \implies \frac{1}{\sqrt{n+2}} < \frac{1}{\sqrt{n+1}}$ (satisfies)
2. $\lim_{n \to \infty} b_n = \lim_{n \to \infty} \frac{1}{\sqrt{n+1}} = 0$ (satisfies)

Thus, this Alternating Series converges. So $x=\frac{1}{3}$ is included.

Therefore, the interval of convergence is $(-\frac{1}{3},\ \frac{1}{3}]$.

Example:

$\sum_{n=0}^{\infty} \frac{n(x+2)^{n}}{3^{n+1}}$

Ratio test:

$\lim_{n \to \infty} \mid \frac{a_{n+1}}{a_n} \mid = \lim_{n \to \infty} \mid \frac{(n+1)(x+2)^{n+1}}{3^{n+2}} \frac{3^{n+1}}{n(x+2)^{n}} \mid$

$= \frac{1}{3} \mid (x+2) \mid \lim_{n \to \infty} \mid \frac{(n+1)}{n} \mid$

$\mid x+2 \mid < 3$ therefore $R=3$

$-3 < x + 2 < 3$

$-5 < x < 1$

Test end points

$x=-5$ :

$\sum_{n=1}^{\infty} \frac{n(-5+2)^{n}}{3^{n+1}} = \sum_{n=1}^{\infty} \frac{n(-3)^{n}}{3^{n+1}}$ diverges

$x=1$, then $\sum_{n=1}^{\infty} \frac{n(1+2)^{n}}{3^{n+1}} = \frac{1}{3} \sum_{n=1}^{\infty} n = \infty$ diverges

Therefore the interval of convergence is $(-5,\ 1)$.

Example:

$\sum_{k=1}^{\infty} (-1)^k \frac{(x-2)^{k}}{2^{k} \sqrt{k}}$

$\lim_{k \to \infty} \mid \frac{(-1)^{k+1}(x-2)^{k+1}}{3^{k+1}\sqrt{k+1}} \frac{3^{k}\sqrt{k}}{(-1)^{k} (x-2)^{k}} \mid$

$\mid x-2 \mid <3$

$-1 < x < 5$

For $x=1$, then $\sum_{k=1}^{\infty} \frac{(-1)^{k}(-1-2)^{k}}{3^{k}\sqrt{k}}$

$= \sum_{k=1}^{\infty} \frac{(-1)^{k}(-3)^{k}}{3^{k}\sqrt{R}} = \sum_{k=1}^{\infty} \frac{1}{\sqrt{k}}$ By the P-Series Test, this diverges

For $x=5$, then $\sum_{k=1}^{\infty} \frac{(-1)^{k}3^{k}}{3^{k}\sqrt{k}}$

$= \sum_{k=1}^{\infty} \frac{(-1)^{k}}{k^{\frac{1}{2}}}$ (Alternating Series)

Alternating Series Test

1. $b_{k+1} < b_{k} \implies \frac{1}{(k+1)^{\frac{1}{2}}} < \frac{1}{k^{\frac{1}{2}}}$ (satisfies)
2. $\lim_{k \to \infty} b_k = \lim_{k \to \infty} \frac{1}{k^{\frac{1}{2}}} = 0$ (satisfies)

Therefore the interval of convergence is $(-1,\ 5]$.

Example (do this yourself):

$\sum_{n=1}^{\infty} \frac{(-1)^{k}7^{k}(x+1)^{k}}{k^{2}}$

$R = \frac{1}{7}$

Interval of convergence: $[-\frac{8}{7},\ -\frac{6}{7}]$

Radius of Convergence - General Form

$\mid x - a \mid < N$. Where $N = R \ \text{(radius of convergence)}$

You must also check endpoints.

Example:

$\mid 3x - 5 \mid < 1$

$3 \mid x - \frac{5}{3} \mid < 1$

$\mid x - \frac{5}{3} \mid < \frac{1}{3}$ therefore $R = \frac{1}{3}$

Example:

$\mid \frac{x}{9} + 5 \mid < 1$

$\frac{1}{9} \mid x + 45 \mid < 1$

$\mid x + 45 \mid < 9$ therefore $R = 9$

Example:

$\mid x - 2 \mid 2 < 1$

Exam 2 Review

Series Manipulations

Example:

$\frac{1}{1-x} = 1 + x + x^{2} + x^{3} + x^{4} + …$ centered at 0.

Now find $\frac{1}{1+x^{2}}$

You can manipulate the known suitable function’s representation

You can replace $x$ by $-x^{2}$ in the $\frac{1}{1-x}$ function:

$\frac{1}{1-\left( -x^{2} \right) } = \frac{1}{1+x^{2}}$

Basically, to get $\frac{1}{1+x^{2}}$, we must replace in $x$ by $-x^{2}$ everywhere in $\frac{1}{1-x} = 1+x+x^{2}+…$. Then $\frac{1}{1+x^{2}} = 1 + \left( -x^{2} \right) + \left( -x^{2} \right) ^{2} + \left( -x^{2} \right)^{3} + \left( -x^{2} \right) ^{4} + …$

$= 1 - x^{2} + x^{4} - x^{6} + x^{8} - …$

Example:

Series to manipulate: $\frac{1}{1-x} = 1 + x + x^{2} + x^{3} + …$

$\frac{x^{2}}{1 + \sqrt{x}}$

$= x^{2} \frac{1}{1+\sqrt{x}} = x^{2} \frac{1}{1-\left( -\sqrt{x} \right)}$

Therefore $= x^{2} \left( 1 + \left( -\sqrt{x} \right) + \left( -\sqrt{x} \right) ^{2} + \left( -\sqrt{x} \right) ^{3} + \left( -\sqrt{x} \right) ^{4} + … \right)$

$= x^{2} \left( 1- x^{\frac{1}{2}} + x - x^{\frac{3}{2}} + x^{2} - x^{\frac{5}{2}} + … \right)$

$= x^{2} - x^{\frac{5}{2}} + x^{3} - x^{\frac{7}{2}} + x^{4} - x^{\frac{9}{2}} + …$

Example:

$\frac{d}{dx} \left( \tan ^{-1} x \right) = \frac{1}{1+x^{2}}$

$\tan ^{-1} x = x - \frac{x^{3}}{3} + \frac{x^{5}}{5} - \frac{x^{7}}{7} + \frac{x^{9}}{9} - \frac{x^{11}}{11}$

Therefore, to get $\frac{1}{1+x^{2}}$, you could differentiate $\tan ^{-1} x$:

$\frac{1}{1+x^{2}} = \frac{d}{dx} \left( x - \frac{x^{3}}{3} + \frac{x^{5}}{5} - … \right)$

$\frac{1}{1+x^{2}} = 1 - x^{2} + x^{4} - x^{6} + x^{8} - x^{10} + …$

Example

Manipulate $e^{x} = 1 + \frac{x}{1!} + \frac{x^{2}}{2!} + \frac{x^{3}}{3!} + …$

Find the Taylor Expansion at $x=0$: $e^{-x^{2}}$

$e^{-x^{2}} = 1 - \frac{x^{2}}{1!} + \frac{x^{4}}{2!} - \frac{x^{6}}{3!} + …$

Example:

Recall that $\cosh x = \frac{e^{x} + e^{-x}}{2}$

We know that:

$e^{x} = 1 + \frac{x}{1!} + \frac{x^{2}}{2!} + \frac{x^{3}}{3!} + …$

$e^{-x} = 1 - \frac{x}{1!} + \frac{x^{2}}{2!} - \frac{x^{3}}{3!} + …$

Find $\cosh x$.

$\cosh x = \frac{e^{x} + e^{-x}}{2} = 1 + \frac{x^{2}}{2!} + \frac{x^{4}}{4!} + …$

Example:

$\ln (1+x) = x - \frac{x^{2}}{2} + \frac{x^{3}}{3} - \frac{x^{4}}{4} + …$

We know that $\frac{1}{1-x} = 1 + x + x^{2} + x^{3} + x^{4} + …$

Replace $x$ by $-x$ in $\frac{1}{1-x} = \frac{1}{\left( - \left( -x \right) \right)} = \frac{1}{1+x}$ and we have:

$\frac{1}{1+x} = 1 - x + x^{2} + x^{4} - x^{5} + …$

$\ln (1+x) = \int \frac{dx}{1+x} = \int \left( 1 - x + x^{2} - x^{3} + x^{4} - x^{5} \right) dx$

$\ln (1+x) = x - \frac{x^{2}}{2} + \frac{x^{3}}{3} - \frac{x^{4}}{4} + \frac{x^{5}}{5} - …$

Example:

$f(x) = \ln \sqrt{1-x^{2}} = \frac{1}{2} \ln \left( 1- x^{2} \right)$

Recall that $\ln (1+x) = x - \frac{x^{2}}{2} + \frac{x^{3}}{3} - \frac{x^{4}}{4}$

Replace:

$= \frac{1}{2} \left( -x^{2} + \frac{x^{4}}{2} - \frac{x^{6}}{3} + \frac{x^{8}}{4} + .. \right)$

$= -\frac{x^{2}}{2} + \frac{x^{4}}{4} - \frac{x^{6}}{6} + …$

Use the first 3 terms of the expansion to find integral: $\int \ln \sqrt{1-x^{2}} dx \approx \int \left( -\frac{x^{2}}{2} + \frac{x^{4}}{4} - \frac{x^{6}}{6} \right) dx$

Then find exact value of $\int_{0}^{1} \ln \sqrt{1-x} dx$

$\frac{1}{2} \int \ln \left( 1-x^{2} \right) dx = \frac{1}{2} \int \ln (1-x) (1+x) dx$

$= \frac{1}{2} \left( \int \ln (1-x) dx + \int \ln (1+x) dx \right)$

$= \frac{1}{2} \left( \int (1-x) d(1-x) + \int \ln (1+x) d(1+x) \right)$

$= \frac{1}{2} \left( -\left( (1-x) \ln (1-x) - (1-x) \right) + \left( (1+x) \ln (1+x) - (1+x) \right) \right)$

$= -0.2 - 0.4 \ln (0.8) + 0.6 \ln (1.2) \approx -0.00134…$

Then, use approximation $\int_{0}^{1} \left( - \frac{x^{2}}{2} + \frac{x^{4}}{4} - \frac{x^{6}}{6} \right) dx = -\frac{x^{3}}{9} + \frac{x^{5}}{20} - \frac{x^{7}}{42} \mid _{0}^{1}$

$= -\frac{1}{6} + \frac{1}{20} - \frac{1}{42} \approx -0.00131…$

Example:

Find $\int_{0}^{0.5} \frac{dx}{1+x^{7}} dx$

You cannot integrate this. Represent this function in terms of power series.

$\frac{1}{1+x^{7}}$

Recall that $\frac{1}{1-x} = 1 + x + x^{2} + x^{3} + x^{4} + …$

$\frac{1}{1+x^{7}} = 1 - x^{7} + x^{14} - x^{21} + x^{28}…$

Approximate the value of the integral $\int_{0}^{0.5} \frac{dx}{1+x^{7}}$ by its Power Series representation by retaining four non-zero terms. Then $\int_{0}^{0.5} \frac{dx}{1+x^{7}} \approx \int_{0}^{0.5} \left( 1 - x^{7} + x^{14} - x^{4} + … \right) dx$

$= x - \frac{x^{8}}{8} + \frac{x^{15}}{15} - \frac{x^{22}}{22} \mid _{0}^{0.5}$

$\approx 0.49951$

NOTE: We cannot find $\int \frac{\sin x}{x} dx$, but we can approximate it by Taylor Series representation

$= \int \frac{x - \frac{x^{3}}{3!} + \frac{x^{5}}{5!}}{x} = \int \left( 1 - \frac{x^{2}}{3!} + \frac{x^{4}}{5!} \right) dx$

Example:

Given $\tan ^{-1}x = x - \frac{x^{3}}{3} + \frac{x^{5}}{5} - \frac{x^{7}}{7} + …$

Find $\int_{0}^{0.1} x \tan ^{-1} \left( x^{2} \right) dx$ by approximating it with Taylor Series representation and retain 3 non-zero terms. Also, find its exact value and compare with approximation.

Approximation:

$x \tan ^{-1} (x^{2}) = x \left( x^{2} - \frac{x^{6}}{3} + \frac{x^{10}}{5} \right) = x^{3} - \frac{x^{7}}{3} + \frac{x^{11}}{5}$

$\int_{0}^{0.1} \left( x^{3} - \frac{x^{7}}{3} + \frac{x^{11}}{5} \right) dx = \frac{0.1^{4}}{4} - \frac{0.1^{8}}{24} + \frac{0.1^{12}}{60} \approx 0.00002499$

Exact:

$\int_{0}^{0.1} x \tan ^{-1}(x^{2}) dx$

$u = \tan ^{-1} (x^{2}) \implies du = \frac{1}{1+x^{4}} 2x dx$

$dv = x dx \implies v = \frac{x^{2}}{2}$

$= \frac{x^{2}}{2} \tan ^{-1}\left( x^{2} \right) - \int \frac{x^{2}}{2} \frac{2x}{1+x^{4}} dx$

$= \frac{x^{2}}{2} \tan ^{-1}\left( x^{2} \right) - \int \frac{x^{3} dx}{1+x^4} dx$

Let $z = 1 + x^{4}$, then $dz = 4x^{3} dx$

$= \frac{1}{3} \int \frac{dz}{z} = \frac{1}{3} \ln (z) = \frac{1}{3}$

$= \frac{x^{2}}{2} \tan ^{-1} x^{2} - \frac{1}{3} \ln (1+x^{4})$

$= \left( \frac{x^{2}}{2} \tan ^{-1} x^{2} - \frac{1}{3} \ln (1+x^{4}) \right) \mid _{0} ^{0.1}$

$= \frac{0.1^{2}}{2} \tan ^{-1} \left( 0.1^{2} \right) - \frac{1}{4} \ln \left( 1 + 0.1 ^{4} \right) \approx 0.00002499$

---

Final Exam

13 Questions

• 3 series

---

Example:

(Exam question)

Use Mac Series of:

$\frac{1}{1-x} = 1 + x + x^{2} + x^{3} + x^{4} + …$

(a) Find the Mac Series of $f(x) = \frac{\sqrt{x}}{1+x}$

And write out the first four non-zero terms.

Solution

Mac Series of $\sqrt{x} = x^{\frac{1}{2}}$ so Mac Series of $f(x) = \frac{x^{\frac{1}{2}}}{1+x+x^{2}+x^{3}+…}$

$f(x) = x^{\frac{1}{2}} - x^{\frac{3}{2}} + x^{\frac{5}{2}} - x^{\frac{7}{2}} + …$

(b) Use the first four non-zero terms from Part (a) to approximate $\int_{0}^{0.25} \frac{\sqrt{x}}{1+x} dx$

Solution

$\int_{0}^{0.25} f(x) dx = \int_{0}^{0.25} x^{\frac{1}{2}} - x^{\frac{3}{2}} + x^{\frac{5}{2}} - x^{\frac{7}{2}} + … dx$

$\frac{2x^{\frac{3}{2}}}{3} - \frac{2x^{\frac{5}{2}}}{5} + \frac{2x^{\frac{7}{2}}}{7} - \frac{2x^{\frac{9}{2}}}{9} \mid _{0}^{0.25}$

$\approx 0.072631448…$

(c) Evaluate $\int_{0}^{0.25} \frac{\sqrt{x}}{1+x} dx$ and thus compare your exact answer with the approximation in Part (b).

Solution

$\int_{0}^{0.25} \frac{\sqrt{x}}{1+x} dx$

Let $u = \sqrt{x}$

$du = \frac{1}{2\sqrt{x}}$

$\int \frac{2u^2}{1+u^2} du$

$2 \left( \int 1 du - \int \frac{1}{1+u^{2}} du \right)$

$2 \left( u - \tan ^{-1} (u) + C \right)$

$\therefore 2\sqrt{x} - 2\tan ^{-1} (\sqrt{x}) \mid _{0}^{0.25}$

$= (0.0727048…) - (0) = 0.0727048…$

Example:

$\sin x = x - \frac{x^{3}}{3!} + \frac{x^{5}}{5!} - \frac{x^{7}}{7!}$

Find the function of the form $a+bx^{n}$ that best approximates $\frac{\sin x - x}{x^2}$.

$f(x) = \frac{\left(x- \frac{x^{3}}{3!} + \frac{x^{5}}{5!} - …\right) - x}{x^{3}} = -\frac{1}{3!} + \frac{x^{2}}{5!} …$

Example:

Radius and interval of convergence of:

$\sum_{k=1}^{\infty} \frac{5^{k}(x-1)^{k}}{k^{2}}$

(a) Radius of convergence

Solution

$\lim_{k \to \infty} \mid \frac{5^{k+1}(x-1)^{k+1}}{(k+1)^{k}} \frac{k^{2}}{5^{k}(x-1)^{k}} \mid$

$= 5 \mid x- 1 \mid \lim_{k \to \infty} \left( \frac{k}{k+1} \right) ^{2} = 5 \mid x-1 \mid <1$

Recall the general form is $\mid x-a \mid < R$

$\mid x-1 \mid < \frac{1}{5}$

(b) Interval of convergence

Solution

$\mid x-1 \mid < \frac{1}{5} \implies -\frac{1}{5} < x < \frac{1}{5}$

$\frac{4}{5} < x < \frac{6}{5}$

Check end points:

$x=\frac{4}{5}$ :

$\sum_{k=1}^{\infty} \frac{5^{k} \left( -\frac{1}{5} \right)^{k} }{k^{2}}$

$\sum_{k=1}^{\infty} \frac{\left( -1 \right) ^{k}}{k^{2}}$

By Alternating Series Test:

• $b_{k+1} < b_k$

$\frac{1}{\left( k+1 \right) ^{2}} < \frac{1}{k^{2}}$ (satisfies)

• $\lim_{k \to \infty} b_k = \lim_{k \to \infty} \frac{1}{k^{2}} = 0$ (satisfied)

Therefore $\sum_{k=1}^{\infty} \frac{\left( -1 \right) ^{k}}{k^{2}}$ converges.

$x=\frac{6}{5}$ :

$\sum_{k=1}^{\infty} \frac{5^{k} \left( \frac{1}{5} \right) ^{k}}{k^{2}}$

$= \sum_{k=1}^{\infty} \frac{1}{k^{2}}$ convergent by the P-Series Test

Therefore the interval of convergence is $[\frac{4}{5};\ \frac{6}{5}]$ (Or $\frac{4}{5} \le x \le \frac{6}{5}$)

---

Exam 2

1 hr 30 minutes

(See exam review packet for more example questions)

• Whenever you see factorials, think ratio test

Question 1

• Given a function where you will estimate Taylor
  • Part a, find the x-order polynomial Taylor
  • from part a, estimate something
  • find the upper bound error

Question 2

• Consider the Taylor Series expansion of $f(x)$
  • Find the constant that best approximates another related function when close to $a$
  • Use your approximation from Part A to estimate the value of a function
  • Write the calculator value

Question 3

• Find the sum of the series (or say it diverges)

Question 4

• Consider the power series
  • Find the radius of convergence of the power series
  • Find the interval of convergence of the power series

Question 5

• Does the series converge or diverge

Question 6

• Use the comparison test, limit comparison test and the ratio test

Question 7

• Use the Taylor Series $f(x)$ to find the Taylor Series for $g(x)$.
  • Find the Taylor series for the anti derivative of $f(x)$. Either use summation mutation or write out the first three nonzero terms
  • Use the first three nonzero terms in your series to approximate an integral
  • Evaluate the actual integral (don’t approximate) and compare your answer with the approximation

---

---

Final Exam

2 hr 30 minutes

Study:

• From Suffolk Homework:
  • Question 11 f

Question 1

• Two indefinite integrals
  • Substitution
  • By parts

Question 2

• Definite integral (Simpsons rule)

Question 3

• Indefinite integral (partial fractions)

Question 4

• improper integral (does it converge/diverge). If it converges, find value

Question 5

• distance/displacement of the particle vector-valued function

Question 6

• setup only
• volume
  • Around the axis
  • Around a shifted axis

Question 7

• setup only
• Mass of the plate
• Find the center of mass (x and y coordinates)

Question 8

• setup only
• Work problem (cone)
• Very similar to midterm question

Question 9

• Taylor polynomials
  • Find 3rd order Taylor polynomial (that is, 4 terms)
  • Find the error (reasonable upper bound)

Question 10

• determine if the series converges/diverges (part a and b)

Question 11

• find Taylor series expansion of the given function
• find the integral of the approximated series
• Just like Question 7 on the second midterm (without Part C)

Question 12

• find the sum of the series (geometric series)

Question 13

• find the radius and interval of convergence of a given power series
• Just like Question 4 on the second midterm

---