The Class

Does not collect homework, however, the quizzes build off the homework assignments. Some sections–about 5–of the homework will be collected and make up of the 5%. Will be graded for completeness.

First quiz will be next Wednesday (the 27th)

This class has a midterm and a final

Midterm is March 11th

Rates of Change and the Derivative

Average Rate of Change

Example 1:

What is the (average) velocity during the 2 min? $\text{avg v} = \frac{\Delta P}{\Delta t} = \frac{1\text{mile}}{\frac{1}{30}h} = 30 mph?$

Speedometer: instantaneous velocity

We will be the average rate of change to approximate the instantaneous rate of change.

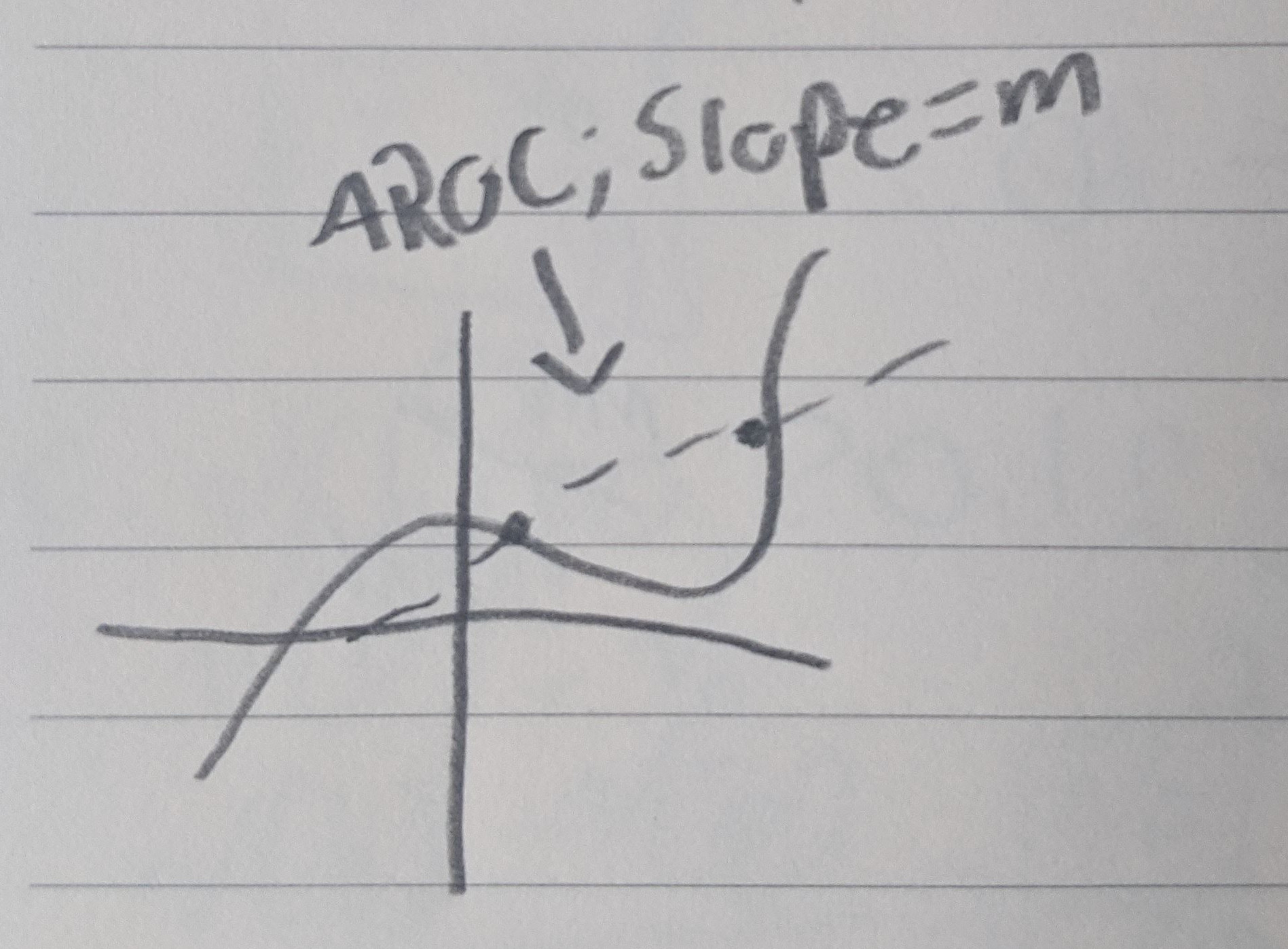
AROC (average rate of change) for $f$ with respect to (wrt) $x$ between $x=a$ and $x=b$ or interval $[a,b]$ where $a<b$.

$\frac{\Delta y}{\Delta x} = \frac{\Delta f}{\Delta x} = \frac{f(b)-f(a)}{b-a}$

This is called the difference quotient.

Example 2:

At times $t=0,\ 1\ 5$ hours, the car is moving $v=30,\ 60,\ 40\ mph$ respectively what are the accelerations between $[0,1],\ [0,5],\ [1,5]$?

Recall: Average acceleration $= \frac{\Delta v}{\Delta t}$

$[0,1]\ a_1=\frac{v(1)-v(0)}{1-0}= \frac{60-30}{1} = 30mph$

$[0,5]\ a_2 = \frac{v(5)-v(0)}{5-0} = \frac{40-30}{5-0} = 2mph$

$[1,5]\ a_3 = \frac{v(5)-v(1)}{5-1} = \frac{40-60}{5-1} = \frac{-20}{4} = -5mph$

Example 3:

What is the AROC of area, $A$, in in$^2$ of 16:9 widescreen TV wrt the diagonal? $d$ (diagonal) between d=32 in d=40in and 40in and 52in?

To solve this, we want $A(d)$

Then we will find $\frac{\Delta A}{\Delta d}$

$A = 16x \times 9x = 337x^{2}$

$(9x)^{2}+(16x)^{2} = d^{2}$

$\therefore 337x^{2} = d^{2}$

$A(d) = \frac{144}{337}d^{2}$

We want $\frac{\Delta A}{\Delta d}$ from [32, 40]

$\frac{\Delta A}{\Delta d} = \frac{A(40) - A(32)}{40-32}$

$\frac{\Delta A}{\Delta d} = \frac{\frac{144}{337}(40^{2}-32^{2})}{8} = \frac{144}{337} * 72 \approx 30.7 \frac{in^2}{in}$

Now do $\frac{\Delta A}{\Delta d}$ from [40, 52]

$\frac{\Delta A}{\Delta d} = \frac{A(52) - A(40)}{52-40} = \frac{\frac{144}{337}(52^2-42^2)}{12} \approx 39.31 \frac{in^2}{in}$

Because these numbers are different for the different ranges, we know that it is dependent on the diagonal.

Ex. 1.1.8

$y=f(x)=4-x^{2}$

What is the AROC of $y$ wrt $x$ on [1,2]

$\frac{\Delta y}{\Delta x} = \frac{\Delta f}{\Delta x} = \frac{f(2) - f(1)}{2-1}$ $= \frac{(4-2^{2}) - (4-1^{2})}{1} = \frac{0-3}{1}=-3$

Def. 1.1.9 - Secant Line

For function $y=f(x)$ and two x values $a$ and $b$. We will define the secant line of $f$ as the line through the points (a, f(a)) and (b, f(b))

Prop 1.1.10 - Slope of Secant Line

Given $y=f(x)$ and $a<b$ the AROC of $f$ on [a,b] is the slope of the secant line of $f$ for $x=a$ and $x=b$.

Instantaneous Rates of Change

Suppose we want the car’s velocity at t=12 min?

If $v = \frac{\Delta p}{\Delta t}$

Solution take average between $t=a$ and $t=a+h$ and let $h$ go to 0.

Def. 1.2.3 - Limit Definition of Derivative

Given $y=f(x)$, the new function $f’$ which is given by $f’(x) = \lim_{\Delta x \to 0} \frac{f(x+\Delta x) - f(x)}{\Delta x} $

$f’(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h}$

This is called the derivative of $f$ with respect to $x$ and is the instantaneous rate of change for any value of $x$ for which the limit exists. This means that if the limit does not exist, the derivative does not either.

Ex. 1.2.2

Recall the 16:9 TV example above.

$A(d) = \frac{144}{337}d^{2}$

What is the derivative (or IROC) of $A$ wrt to $d$ when $d=40in$?

$A’(d) = \lim_{h \to 0} \frac{A(d+h) - A(d)}{h}$

$= \lim_{h \to 0} \frac{\frac{144}{337}(d+h)^{2} - \frac{144}{337}d^{2}}{h}$ $= \lim_{h \to 0} \frac{144}{337} \frac{d^{2}+2dh+h^{2} - d^{2}}{h}$

$A’(d) = \lim_{h \to 0} \frac{144}{337} \frac{h(2d+h)}{h} = \frac{144}{337} 2d$

$A’(40) = \frac{144}{337} 2(40) \approx 34.2 \frac{in^{2}}{in}$

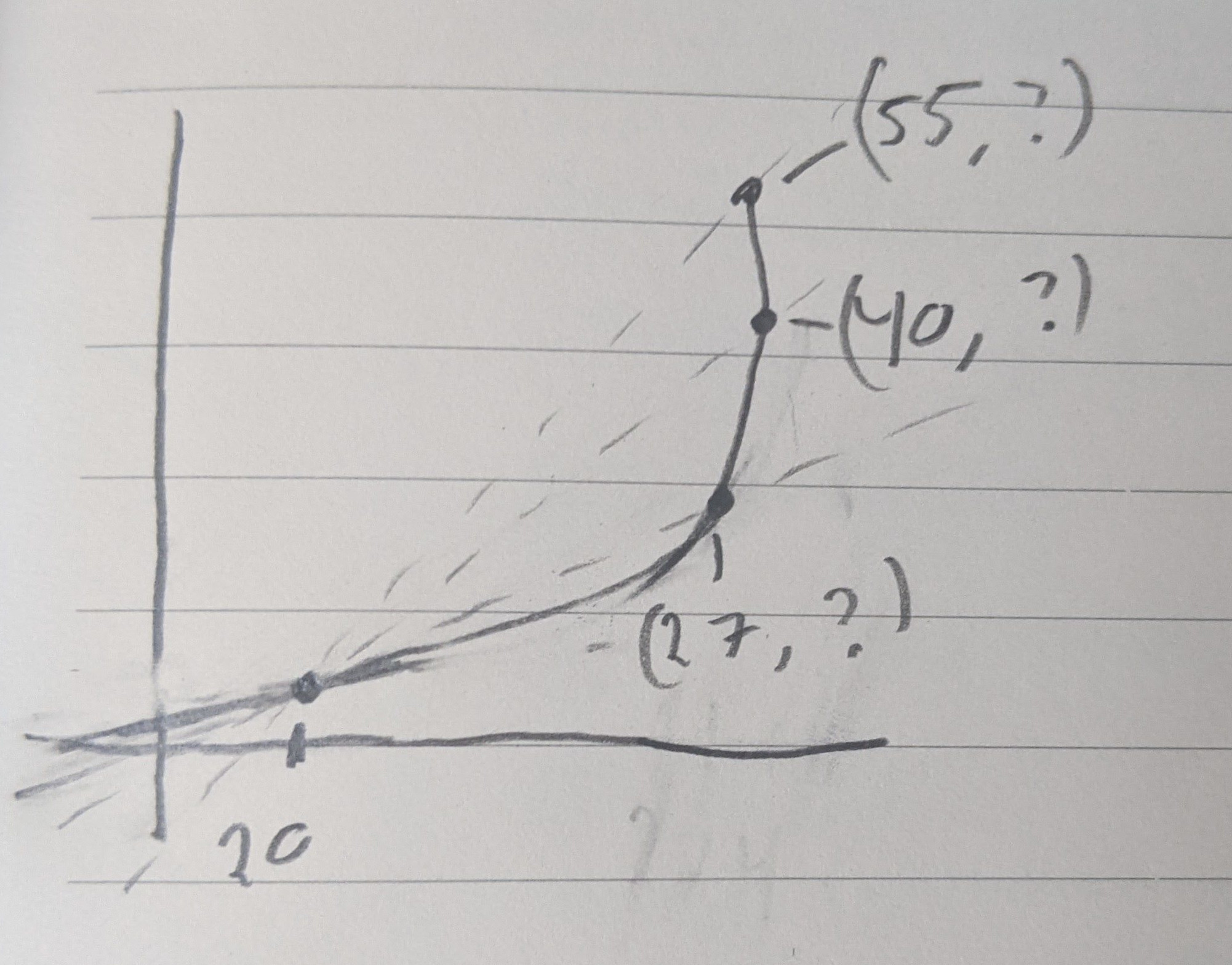
Secant Line:

Consider a function with secant-lines (20, 55), (22,40), (20, 27)

The smaller the interval, the closer it becomes to the instantaneous rate of change.

Recall: $A’(d) = \frac{144}{337} 2d$

IROC of $A$ wrt $d$ at 20, $A(20)$=tangent to the graph at that point.

What is the equation of the tangent line?

$A(20) = A’(20)(d-20)$ $A-170.92 = 17.09(d-20)$

Recall:

Point-slope Form

$y-y_1 = f’(x_1)(x-x_1)$

Given particle with position $p(t) = \frac{1}{\sqrt{t}}$ for $t>0$ what the velocity?

$p’(t) = v(t) = \lim_{h \to 0} \frac{p(t+h)-p(t)}{h}$ $= \lim_{h \to 0} \frac{\frac{1}{\sqrt{t+h} }-\frac{1}{\sqrt{t}}}{h}$

$p’(t) = \lim_{h \to 0} \frac{\frac{1 * \sqrt{t}}{\sqrt{t+h} * \sqrt{t}}- \frac{1 * \sqrt{t+h} }{\sqrt{t} \sqrt{t+h} }}{h}$

$p’(t) = \lim_{h \to 0} \frac{1}{h} \frac{\sqrt{t} -\sqrt{t+h} }{\sqrt{t+h} \sqrt{t} } \frac{\sqrt{t} + \sqrt{t+h} }{\sqrt{t} +\sqrt{t+h} }$

$p’(t) = \lim_{h \to 0} \frac{1}{h} \frac{t-(t+h)}{\sqrt{t+h} \sqrt{t} (\sqrt{t} + \sqrt{t+h} )}$

$p’(t) = \frac{-1}{t * 2 * \sqrt{t} }$

1.3 Limits and Continuity

Quiz is going to be on sections 1, 2, 3 on Wednesday 1/27

$f(x) = \sin(x)$

$f(x) = \frac{1}{x}$

Consider:

$f(x) = \frac{\sin(x)}{x}$

$f(1) = 0.84$

$f(0.2) = 0.993$

…

So we can say:

$\lim_{x \to 0^+} \frac{\sin(x)}{x} = 1$

$\lim_{x \to 0^-} \frac{\sin(x)}{x} = 1$

When $\lim_{x \to 0^-} = \lim_{x \to 0^+}$ are the same, we say that the two-sided limit exists.

But $\frac{\sin(0)}{0} = \frac{0}{0}$ so we can’t just do that.

Consider this graph

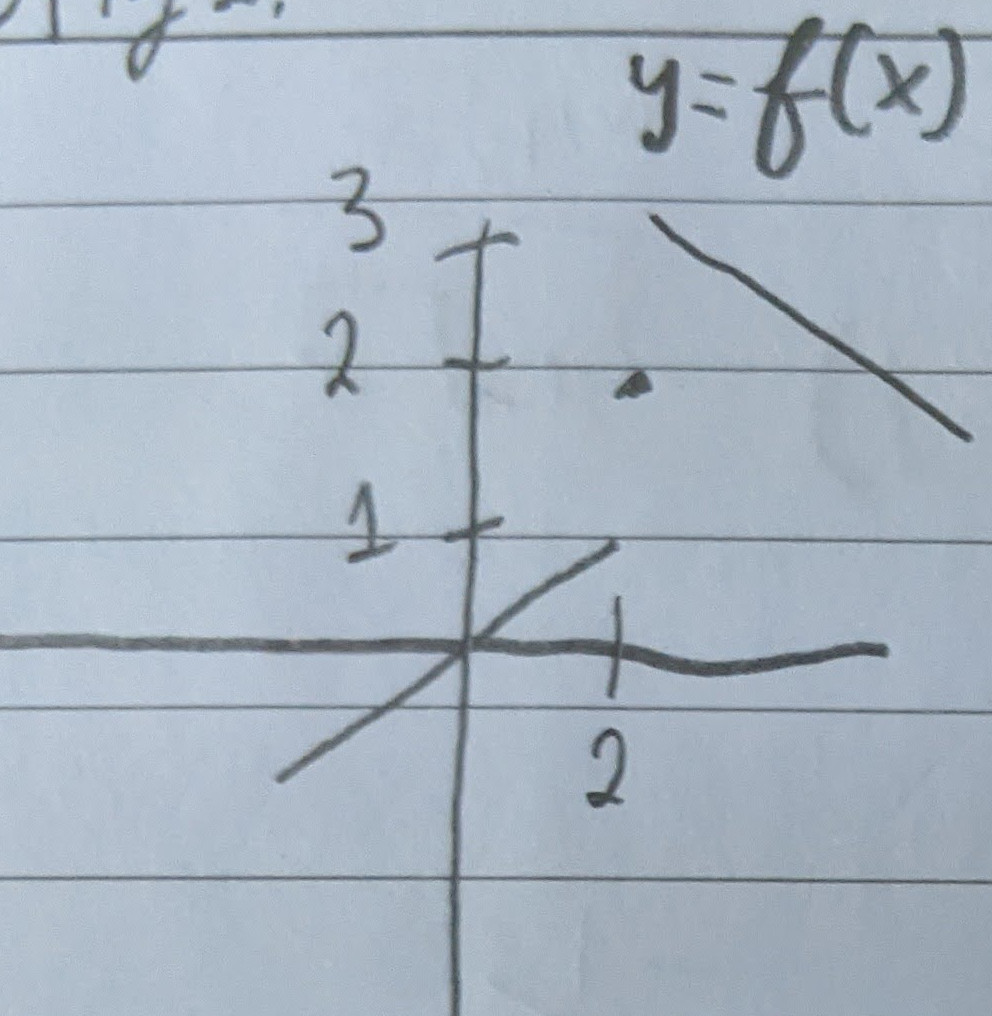
$\lim_{x \to 2^-} f(x) = 1$

$\lim_{x \to 2^+} f(x) = 3$

$\lim_{x \to 2} f(x) = DNE$

$\lim_{x \to 6^-} f(x) = 1$

$\lim_{x \to 6^+} f(x) = DNE$

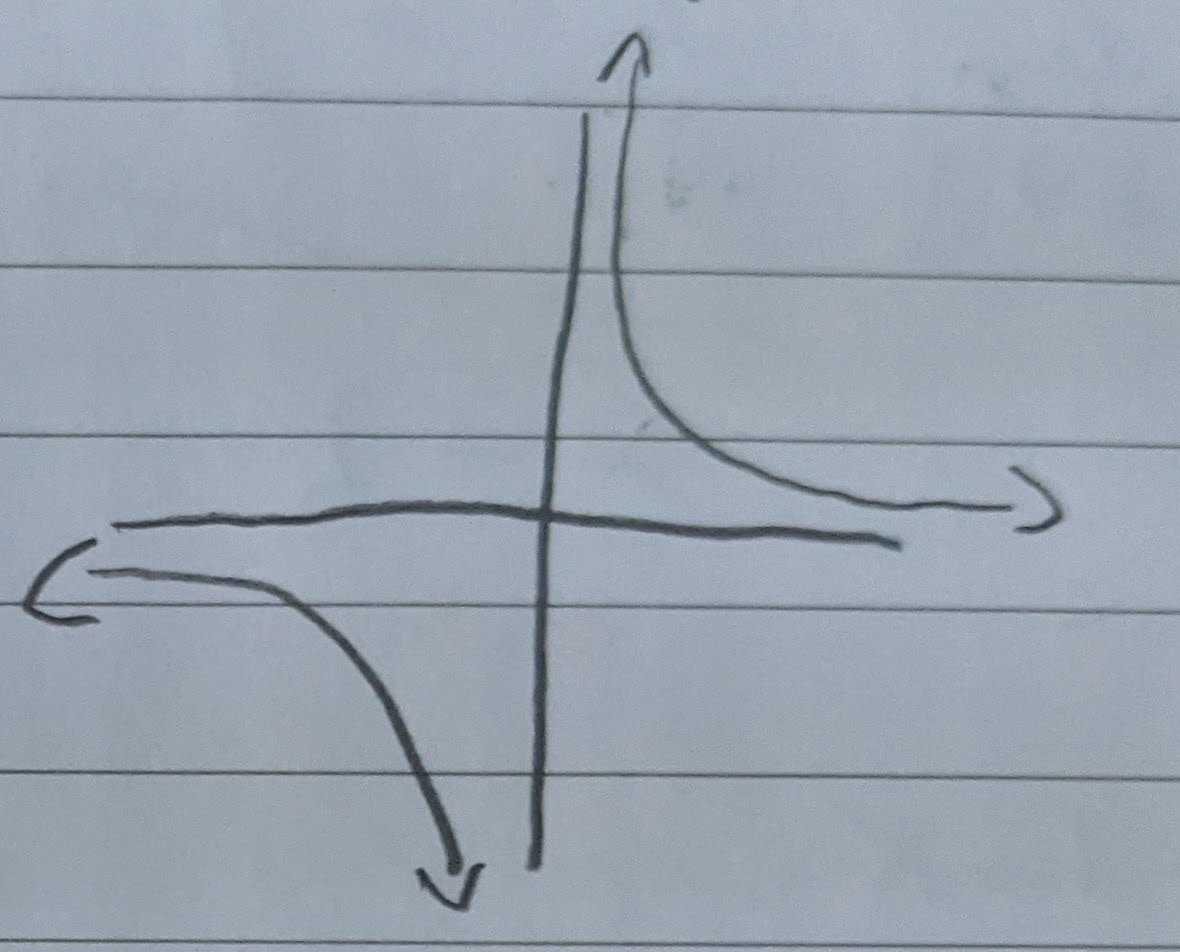
$\lim_{x \to 0^+} f(x) = +\infty$

$\lim_{x \to 0^-} f(x) = -\infty$

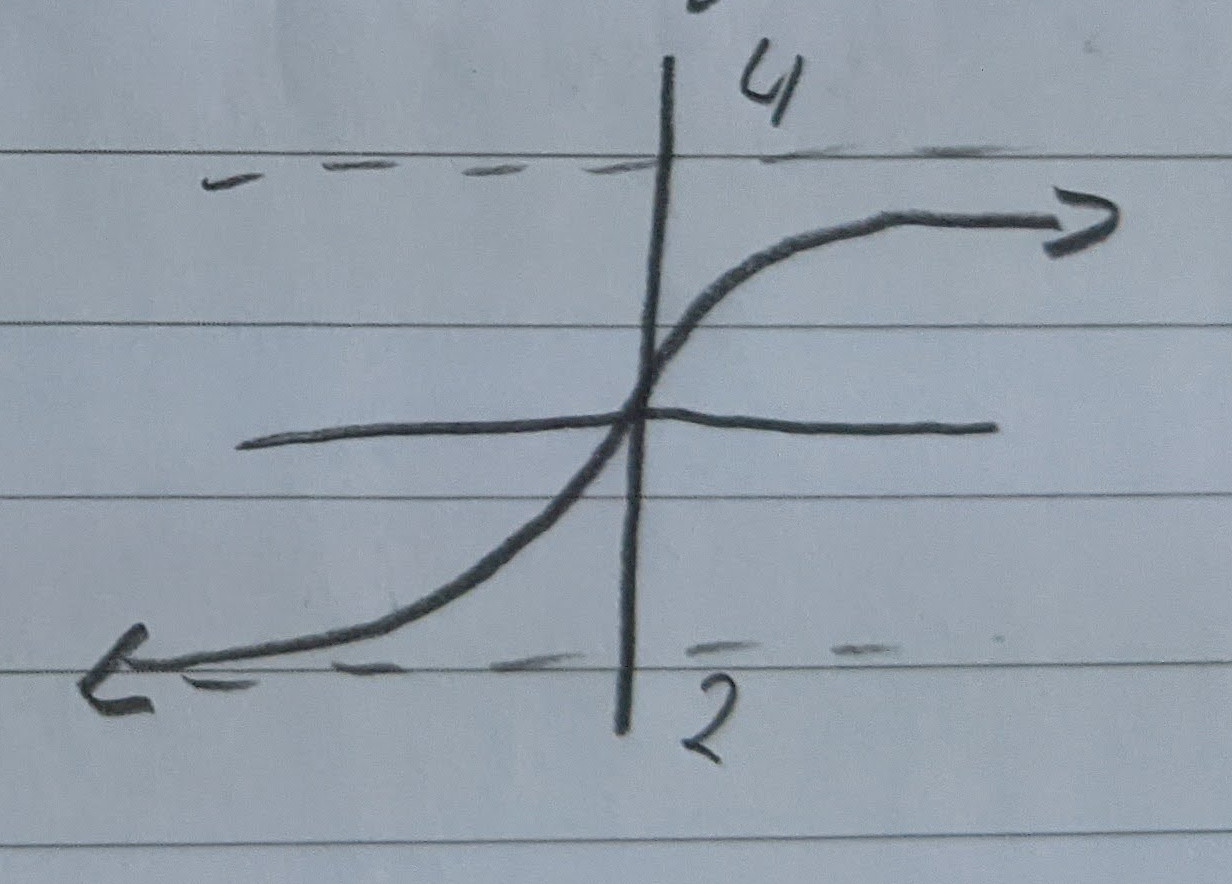
$\lim_{x \to \infty} f(x) = 4$

$\lim_{x \to \infty} f(x) = -2$

Theorem 1.3.15: Limit Rules

Suppose $\lim_{x \to b} f(x) = L_1$ and $\lim_{x \to b} g(x) = L_2$ and $c$ is a real number.

The Limit of the constant $f_n$ -> the constant
$\lim_{x \to b} c * f(x) = c * L_1$
$\lim_{x \to b} [f(x) + g(x)] = L_1 + L_2$
$\lim_{x \to b} f(x)*g(x) = L_1 * L_2$
If $L_2 \neq 0$ then $\lim_{x \to b} \frac{f(x)}{g(x)} = \frac{L_1}{L_2}$

Example 1:

$\lim_{x \to 2} g(x) = 4x^{3}-5x+7$ $= 4 \lim_{x \to 2} x^{3} - 5 \lim_{x \to 2} x + \lim_{x \to 2} 7$

$= 4(\lim_{x \to 2} x * \lim_{x \to 2} x * \lim_{x \to 2} x) - \lim_{x \to 2} x + 7 $ (now just substitute)

$= 29$

Example 2:

$\lim_{x \to 2} \frac{x^{2}-4}{x-2} = \lim_{x \to 2} \frac{(x-2)(x+2)}{x-2} = \lim_{x \to 2} (x+2) = 4$

Example 3:

$\lim_{x \to 1} \frac{\frac{1}{\sqrt{x} }-1}{x-1} = \lim_{x \to 1} \frac{1-\sqrt{x} }{\sqrt{x} (x-1)} * \frac{1+\sqrt{x} }{1+\sqrt{x} }$

$\lim_{x \to 1} \frac{1-x}{\sqrt{x} (x-1)(1+\sqrt{x} )} = \lim_{x \to 1} \frac{-1}{\sqrt{1} (1+\sqrt{1} )} = \frac{-1}{2}$

Continuity

If $\lim_{x \to a} f(x) = f(a)$ then we say that $f(x)$ is continuous. (We want this because continuous functions have derivatives.)

Discontinuous Functions have the following:

Holes
Jumps
Asymptote
Removable lack of continuity

1.4 Instantaneous Rates of Change: The Derivative

Homework is going to be collected

Limit Definition of the Derivative

$f’(x) = \lim_{\Delta x \to 0} \frac{f(x+\Delta x) - f(x)}{\Delta x}$

$= \lim_{h \to 0} \frac{f(x+h)-f(x)}{h}$

Notation:

$f’, y’, \frac{dy}{dx}$

$\frac{dy}{dx} \mid _{x=a}$ means $f’(a)$

Propositions:

Suppose $c$ is a constant and $f$ is differentiable at $x$ then $cf$ is also differentiable at x and $f’(cx) = cf’(x)$.

Suppose $f$ and $g$ are differentiable at $x$ then $f+g$ is differentiable at $x$ and $(f+g)’(x) = f’(x)+g’(x)$ (or $\frac{d}{dx}(f+g) = \frac{df}{dx}+ \frac{dg}{dx}$).

Examples:

Example 1:

Find the derivatives $w’, y’, z’$ and evaluate at $x=1$ for $w=f(x)=c$, $y=g(x)=x$ and $z=m(x)=x^{2}$.

$w’= \lim_{h \to 0} \frac{f(x+h)-f(x)}{h} = \lim_{h \to 0} \frac{c-c}{h}=0$
$y’= \lim_{h \to 0} \frac{g(x+h)-g(x)}{h}= \lim_{h \to 0} \frac{x+h-x}{h} = \lim_{h \to 0} \frac{h}{h} = 1$
$z’=\lim_{h \to 0} \frac{m(x+h)-m(x)}{h}= \lim_{h \to 0} \frac{(x+h)^{2}-x^{2}}{h} = \lim_{h \to 0} \frac{x^{2}+2xh+h^{2}-x^2}{h} = \lim_{h \to 0} 2x+h = 2x$
$w’(1) = 0$
$y’(1) = 1$
$m’(1) = 2(1) = 2$

Slope-point form: $y-y_1 = f’(x_1)(x-x_1)$

Example 2:

A particle has velocity given by $v = \frac{1}{2\sqrt{t+2} }$ for $t>2$. Find the acceleration.

Answer: $\frac{-1}{4(t+2)^{3/2}}$ HINT: The trick for radicals is multiply by the conjugate.

Differentiability

If $f$ is differentiable at $x$ then $f$ is continuous at $x$.

If $f$ is not continuous at $x$ then $f$ is not differentiable at $x$.

Places where $f$ can fail to be differentiable:

Breaks/Jumps
Corners or cusps
- Example $f(x) = \mid x\mid $
Vertical tangents

Exercise 19.

Find equations of tangent lines of $f$ at given points

$r(x) = \frac{1}{1+x}$, $x=0,1,2$

$r’(x) = \frac{-1}{(1+x)^{2}}$

$r(0) = 1$
$r(1) = \frac{1}{2}$
$r(2) = \frac{1}{3}$
$r’(0) = -1$
$r’(1) = \frac{-1}{4}$
$r’(2) = \frac{-1}{9}$

Recall Slope-point form: $y-y_1 = f’(x_1)(x-x_1)$

$y-1 = -1(x-0) = y-1 = -x$
$y-\frac{1}{2} = \frac{-1}{4}(x-1)$
$y-\frac{1}{3} = \frac{-1}{9}(x-2)$

1.5 Extrema and the Mean Value Theorem

Extrema

Extreme values – maximum or minimum

Recall:

$f(x) = x^{2}$

$f’(x) = 2x$

$f’(2) = 2(2) = 4$
$f’(-2) = 2(-2) = -4$

We know that this function makes one turn (at point x=0). That’s it’s absolute minimum

Consider $g(x)$:

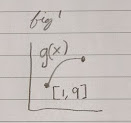
does this have a minimum and maximum? Yes!

Consider $h(x)$ :

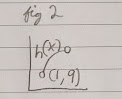
Does this have a minimum and maximum?

No! You can always get closer

But you can have local max and min:

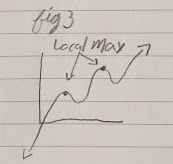
You can also have local min and global(/absolute) min:

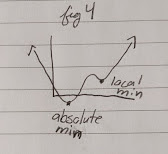
Local Extrema: Larger/smaller than its neighbors

Global/Absolute Extrema: The largest/the smallest value in the entire function

Extreme Value Theorem

if a $f$ is continuous on $[a,b]$, then $f$ has both a maximum and a minimum on $[a,b]$

Theorem 1.5.4

If $f$ is differentiable at $x$ and obtains a local extreme value at $x$, then $f’(x)=0$.

Definition - Critical Point:

For a function, a critical point is any value $x$ such that $f’(x)=0$ or $f’(x)$ does not exist.

A critical value of $f$ is the value of $f$ at the critical point.

If $f$ attains a local extreme value at $x$ then $x$ must be a critical point.

To find extreme values in $[a,b]$:

Find the critical points in $(a,b)$
Evaluate $f$ at critical points and the end points a and b
Largest=max, smallest=min

Examples

Find global max and min of $f(x)=2x^{3}-15x^{2}+36x$ on $[1,5]$ and determine where they occur:

$f’(x) = 6x^{2}-30x+36$

$f’(x) = 0 = 6(x^{2}-5x+6)$

$0=x^{2}-5x+6$

$0=(x-3)(x-2)$

$\therefore f’(x) = 0 \text{ when } x=3,2$

$f(1) = 23$

$f(2) = 28$

$f(3) = 27$

$f(5) = 55$

Therefore, our global max is 55 and our global min is 23.

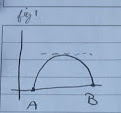
Mean Value Theorem

Mean Value Theorem (for derivatives)

If $f$ is differentiable over $[a,b]$ then at some point $c$ between $a+b$:

$\frac{f(b)-f(a)}{b-a} = f’(c)$

Rolle’s Theorem:

Consider another example:

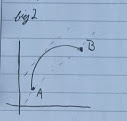
$f(b)-f(a) = f’(c)(b-a)$

(assume b>a)

if $f’(c) > 0 \implies f(b) > f(a)$ which means that the function is increasing.

if $f’(c) < 0 \implies f(b) < f(a)$ which means that the function is decreasing

If we are decreasing on one side and increasing on another, we have a local min.

If we are increasing on one side and decreasing on another, we have a local max.

First Derivative Test for Extrema

Suppose $c$ exists in our interval $(a,b)$ if $f’(x) > 0$ from $(a,c)$ and $f’(x) < 0$ from $(c,b)$, then $c$ is a local max. Vice versa is a local min.

Each critical point, the behavior of the function is changing.

Consider this example:

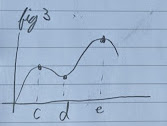
The behavior is the same in these intervals

$(-\infty, c)$
$(c,d)$
$(d,e)$
$(e,\infty)$

For the actual behavior in arbitrary points in these intervals, test the derivative. For the actual min and max, test the function.

Example:

Find a value of $c$ such that the conclusion of the mean value theorem is satisfied for $f(x) = -2x^{3}+6x-2$ on $[-2,2]$
Find the global extrema for our function on $[-2, 2]$
Find the local extrema and behavior of $f$ on $[-2, 2]$

Proving the mean value theorem (visualization):

Recall: $f(b)-f(a) = f’(c) (b-a)$

1.6 Higher Order Derivatives

Examples

Find the relative extrema and behavior of $f(x) = x^{3}$.

$f’(x) = 3x^{2} = 0$

$\therefore x=0$

Intervals:

$(-\infty, 0)$ $f’(-1) = +3$ increasing
$(0, \infty)$ $f’(1) = +3$ increasing

There are no extreme values:

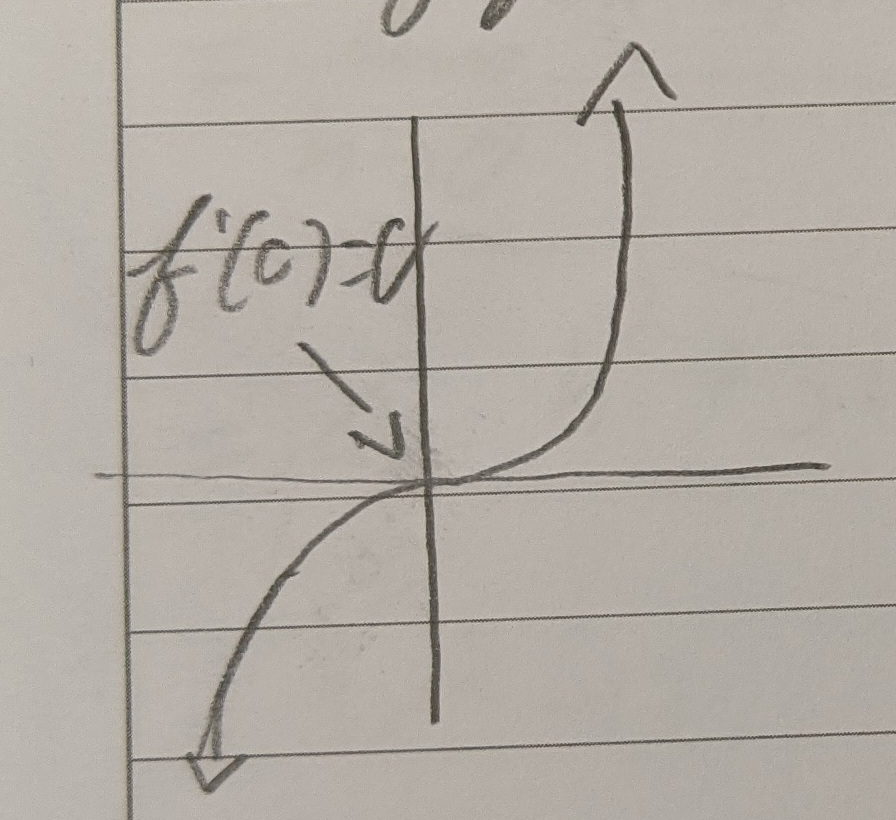
Position:

1st derivative: velocity

Tangent line at a point

2nd derivative: acceleration

3rd derivative: jerk (we won’t use it)

Consider this function:

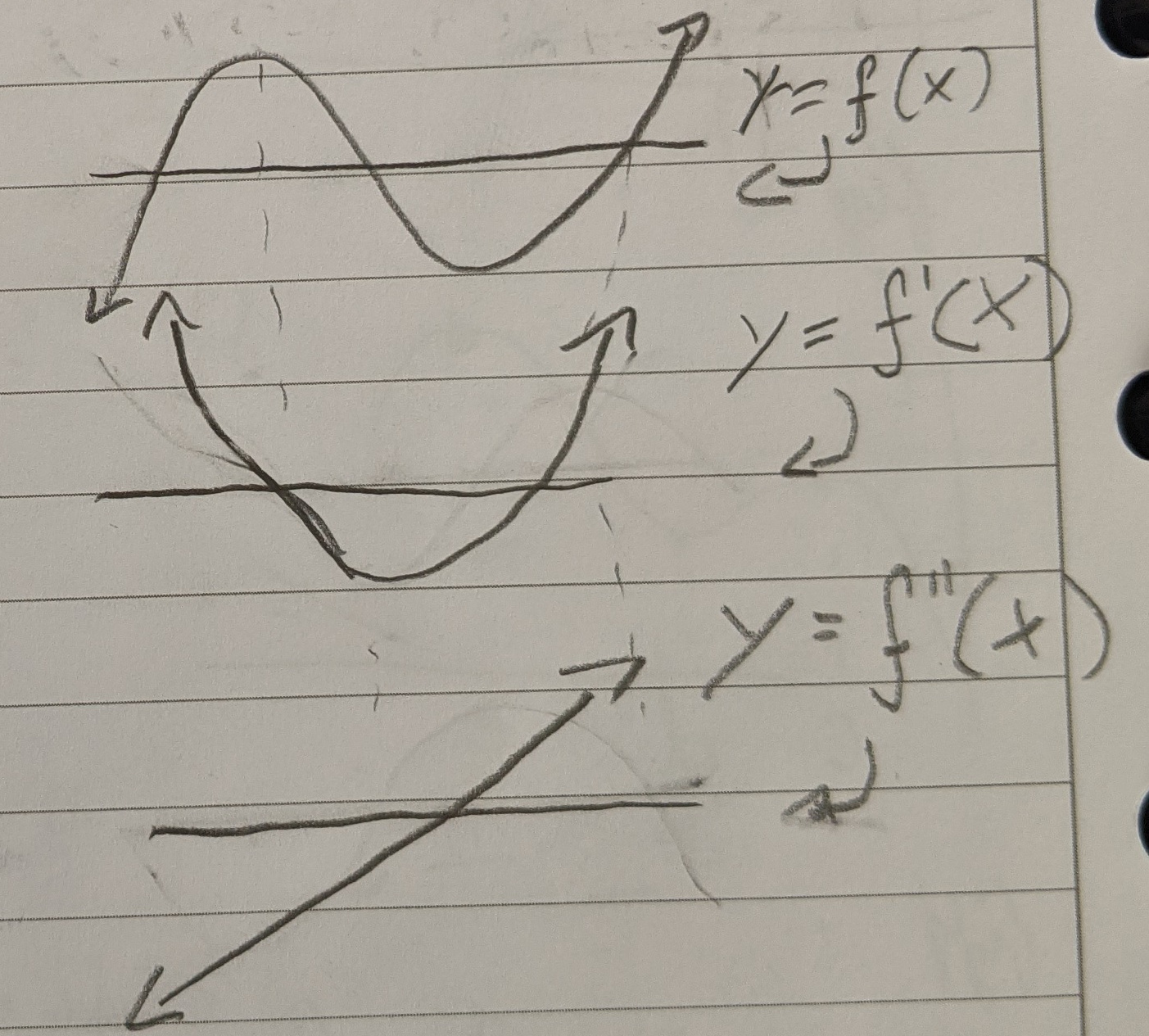
If $f’‘<0$ then $f$ at that point is concave down

And if $f’=0$ then it’s a local max

If $f’‘>0$ then $f$ at that point is concave up

And if $f’=0$ then it’s a local min

Definition - Concave

The graph of $f$ is concave up on an interval if $f’‘(x)$ exists and is greater than 0 (on the interval).

The graph of $f$ is concave down on an interval if $f’‘(x)$ exists and is less than 0 (on the interval).

If the concavity switches at $x=b$ then we have an inflection point at $b$ (assume $b$ is in the domain of $f$).

So if $f’’$ switches from positive to negative, the inflection point is at 0.

Theorem 1.6.9 - 2nd Derivative Test for Extrema

Suppose $f’(c)=0$. If $f’‘(c)>0$, $f$ attains a local min at point $c$. If $f’‘(c)<0$, $f$ attains a local max at point $c$.

Example

$f(x) = 2x^{3}-15x^{2}+36x$

$f’(x) = 6x^{2}-30x+36$

$f’(x) = (x-3)(x-2)=0$

Critical points:

$x=2,3$

So $f’‘(x)=12x-30$

$f’‘(2)=12(2)-30=-6<0 \therefore$ local max

$f’‘(3)=12(3)-30=+6>0 \therefore$ local min

Steps for the solution:

Find the extreme values
Find the intervals of concavity and any points of inflection $f’‘(x) = 0 \therefore x=\frac{5}{2}$

So $x=2.5$ is a possible point of inflection

Intervals: $(-\infty, 2.5), (2.5, \infty)$

$f’‘(2) = -6$ concave up

$f’‘(3) = +6$ concave down

Therefore $x=2.5$ is a point of inflection.

If we have a polynomial, the points of concavity and the points of inflections are NEVER the same.

Example:

Calculate the concavity and extrema of $f(x)=\frac{1}{3}x^{3}-2x$

$f’(x)=x^{2}-2=0 \therefore x=-\sqrt{x}, \sqrt{x} $

$f’‘(x)=2x = 0 \therefore x=0$ possible inflection point at $x=0$

$f’’(-\sqrt{2}) = -2*\sqrt{2} $ because it’s negative, it’s a local max

$f’’(\sqrt{2}) = 2*\sqrt{2} $ because it’s positive, it’s a local min

Because it goes from positive $f’’$ to negative, $x=0$ is a point of inflection.

Behavior:

$(-\infty, -\sqrt{2}) $ positive
$(-\sqrt{2}, \sqrt{2}) $ negative
$(\sqrt{2}, \infty)$ positive

Example: (practice)

Find the points of inflection, intervals of concavity, extrema, and behavior of $f(x)=x^{4}-4x^{3}+2$

$f’(x) = 4x^{3}-12x^{2}$

$f’(x) = 0 = 4x^{2}(x-3)$

$\therefore x=0, 3$ are critical points

Intervals:

$(-\infty, 0)$ $f’(-1) = -16 \therefore$ decreasing
$(0, 3) f’(1) = -8 \therefore$ decreasing
$(3,\infty) f’(4) = 64 \therefore $ increasing

This means that $x=0$ is not an extrema. $x=3$ is a local min.

Second Derivative Test:

$f’‘(0) = 0$ inconclusive!

$f’‘(3) = 36 > 0 \therefore x=3$ is a local min

$f’‘(x) = 12x^{2}-24x$

$f’‘(x) = 0 = 12x(x-2)$

$\therefore x=0, 2$ these are possible points of inflection

$f’’(-1) = 36$ positive

$f’‘(1) = -12$ negative

$f’‘(3) = 36$ positive

Because they switch every value of $x=0, 2$, 0 and 2 are points of inflection.

2.0 Rules for Derivative

Recall: $(x^{2})’ = 2x$

Theorem 2.1.1 Power Rule for Natural Exponents

Suppose $n$ is a positive integer, then $(x^n)’ = n x^{n-1}$. Note: when $n=1$, $x^{0}=1=constant$.

Given $f(x)=x^{n}$, $f’(x) = \lim_{h \to 0} \frac{f(x+h)-f(x)}{h} = \lim_{h \to 0} \frac{(x+h)^{n}-x^{n}}{h}$.

Consider if $n=2$, the first part of the numerator would be: $x^{2}+2xh+h^{2}$

Consider if $n=3$, the first part of the numerator would be: $x^{2}+3x^{2}h+3xh^{2}+h^{3}$

Both have a common form: $x^{n}+nx^{n-1}h+h^{2} p(x,h)$ (p as in polynomial)

$f’(x) = \lim_{h \to 0} \frac{x^{n}+nx^{x-1}h+h^{2}p(x)h - x^{n}}{h}$

$f’(x) = nx^{n-1} + p(x,h) = nx^{n-1}$

Example:

$g(x) = \frac{d}{dt}(5t^{3}-\sqrt{7} t^{2})$

$g(x) = 5 \frac{d}{dt}t^{3} - \sqrt{7} \frac{d}{dt}t^{2}$

$g(x) = 15 ^{2} - 2\sqrt{7} t$

Example:

$f(x) = x^{3}$

$f’(x) = 3x^{2} = 0 \therefore x=0$

This, however, does not mean that we have a local or global extrema at this point.

2.1 The Power Rule and Linearity

Topic: Summation Notation

Consider a real function $B$ that has terms from I=m to n. What does the sum of its terms look like?

$B(m) + B(m+1) + … + B(n-1) + B(n) = \sum_{i=m}^{n} B(i)$

Example:

$\sum_{i=-1}^{3} i^{2} = (-1)^{2} + (0)^2 + (1)^2 + (2)^2 + (3)^2 = 15$

Theorem 2.1.8 Derivative of Polynomial Summations

Suppose $p(x)$ is a polynomial function

$p(x) = a_0 + a_1 * x + a_2 x^2 + … + a_{n-1}x^{n-1} + a_n x^n = \sum_{i=0}^{n} a_ix^i$

Then $p’(x) = a_1 + 2a_2x + … a_{n-1}(n-1)x^{n-2} + a_{n}nx^{n-1} = \sum_{i=1}^{n} a_i i x^{i-1}$

2.2 The Product and Quotient Rule

Theorem: Suppose $f$ and $g$ are differentiable at $x$.

Then:

The product rule:

$f(x) * g(x)$ is differentiable

$(f*g)’(x) = f(x) g’(x) + f’(x) g(x)$

Quotient Rule: $f g(x) \neq 0$

$\frac{f}{g}$ is differentiable at $x$ and $\left( \frac{f}{g} \right)’ (x) = \frac{g(x) f’(x) - f(x) g’(x)}{(g(x))^{2}}$

NOTE: We rarely want to expand the $(g(x))^{2}$ in the denominator.

Example:

$f(x) = \frac{1}{x-1}$

$f’(x) = \frac{(x-1)*0 - 1(1)}{(x-1)^2} = \frac{-1}{(x-1)^{2}}$

Don’t expand the bottom!

Example:

$g(v) = (5v^{2}-2v)(v^7 + 2)$

Find $g’(v) = 45v^8 + 20v - 16v^7 - 4$

Example:

Calculate: $\left( \frac{w^3 + 4w}{w-1} \right)’ = \frac{2w^3 - 3w^2 -4}{(w-1)^2}$

Power Rule for Integers

For all $x$ in the domain of $x^n$, $\left( x^n \right)’ = n x^{n-1}$.

Proof For for $n \le -1$

i.e. when $n=-m$ and $m\ge 1$

Quotient Rule: $\left( \frac{1}{x^{m}} \right) = \frac{x^m * 0 - mx^{m-1}}{(x^m)^2} = mx^{m-1-2m} = mx^{-m-1} = nx^{n-1}$

Example:

Find the critical points and intervals of increasing and decreasing for $f(x) = \frac{x^2 -2x -1}{2x-5}$

Recall the quotient rule.

$f’(x) = \frac{2(x-2)(x-3)}{(2x-5)^{2}}$

Therefore the critical points are: 2, 2.5 (because it doesn’t exist), and 3. Also the function doesn’t exist at 2.5.

Interval:

NOTE: We only test the numerator because the denominator is squared and therefore always positive

$(-\infty, 2) f_a’(0) = 2(0)^2 - 10(0) + 12 = 12$ positive
$(2, 2.5) f_a’(2.4) = 2(2.4)^2 - 10(2.4) + 12 = -0.48$ negative
$(2.5, 3) f_a’(2.75) = 2(2.75)^2 - 10(2.75) + 12 = -0.375$ negative
$(3, \infty) f_a’(5) = 2(5)^2 - 10(5) + 12 = 12$ positive

Therefore:

2 is a local max
3 is a local min

Example:

Given the equation for the tangent line to the graph of $y=f(x)$ at given points.

$f(x) = \frac{1}{1+x^n}; (1, \frac{1}{2})$

$f’(x) = \frac{-nx^{n-1}}{(1+x^n)^2}$

$f(1) = \frac{1}{2}$

$f’(1) = \frac{-n * 1^{n-1}}{(1+1^n)^2}$

$f’(1) = \frac{-n}{4}$

$y-\frac{1}{2} = \left( \frac{-n}{4} \right) (x-1)$

2.3 The Chain Rule

Suppose $g$ is differentiable at $x$ and $f$ is differentiable at $g(x)$. Then, $f(g(x))$ is differentiable at $x$ and $(f(g(x)))’ = f’(g(x)) * g’(x)$

Leibniz Notation:

Suppose $u=g(x)=2x$ and $y=f(u)=\sin(u)$. We want $\frac{dy}{dx} = \frac{dy}{du} * \frac{du}{dx} = \frac{d}{dx} \sin(2x) = \cos(2x) * 2$.

This can also be expanded:

$\frac{dy}{dz} = \frac{dy}{du} * \frac{du}{dx} * \frac{dx}{dr} * \frac{dr}{dz}$

Example:

Consider $f(x) = x^{3}$ and $g(x) = 2x^{2}$. This can be represented as $(f \bullet g)(x)$

$h(x) = f(g(x)) = \left( 2 x^{2} \right) ^{3}$

$h’(x) = f’(g(x)) * g’(x) = 3(2x^{2})^{2} * 2 * 2x = 48x^{5}$

Example:

Differentiate: $((x^{2}+1)^{2} + 2x^{3})^{4}$

$= 4 ((x^{2}+1)^2 + 2x^{3})^{3} * (2(x^{2}+1) * 2x + 6x^{2})$

Example:

$V = \frac{4}{3}\pi R^{3}$

We are given $\frac{dV}{dt} = 64 \frac{in^{3}}{s}$

At what rate is the radius increasing when the radius is 3 in?

NOTE: All of our rates are with respect to time.

We are looking for $\frac{dR}{dt} \mid _{R=3in}$

$\frac{dV}{dt} = \frac{dV}{dR} * \frac{dR}{dt} = 4\pi R^{2} * \frac{dR}{dt}$

$\frac{dR}{dt} = \frac{1}{4\pi R^{2}} * \frac{dV}{dt}$

$\therefore \frac{dV}{dt} = \frac{1}{4\pi (3in)^{2}} 64 \frac{in^{3}}{s}$

$= \frac{16}{9\pi} \frac{in}{s} \approx 0.566 \frac{in}{s}$

Example

$z = \frac{1}{\sqrt{5w^{2}-7w} }$ find $\frac{dz}{dw}$

$= (5w^2 - 7w)^{\frac{-1}{2}}$

$\frac{dz}{dw} = \frac{-1}{2} (5w^2 - 7w)^{\frac{-3}{2}} * (10w - 7)$

$= \frac{-(10w-7)}{2(5w^2-7w)^{\frac{3}{2}}}$

Chain Rule to Find Derivative of a Rational Power

Consider $f^{-1}(x) = x^{\frac{1}{3}}$ and $f(x) = x^3$

$f(f^{-1}(x)) = x$

Differentiate:

$f’(f^{-1}(x)) * f^{-1}’(x) = 1$

$\therefore (f^{-1}(x))’ = \frac{1}{f’(f^{-1}(x))} = \frac{1}{3(f^{-1}(x))^2}$

$= \frac{1}{3 x^{\frac{2}{3}}}$

Power Rule for Rational Powers

for $r$ rational and $x$ in the domain of $x^r$, then $x \neq 0$ the $f(x) = x^r$ is differentiable at $x$ and $(x^r)’ = rx^{r-1}$

Inverse Functions

An inverse of function is just the function reflected over the line $y=x$.

$f’ = \frac{\Delta y}{\Delta x}$

$(f^{-1})’ = \frac{\Delta x}{\Delta y}$

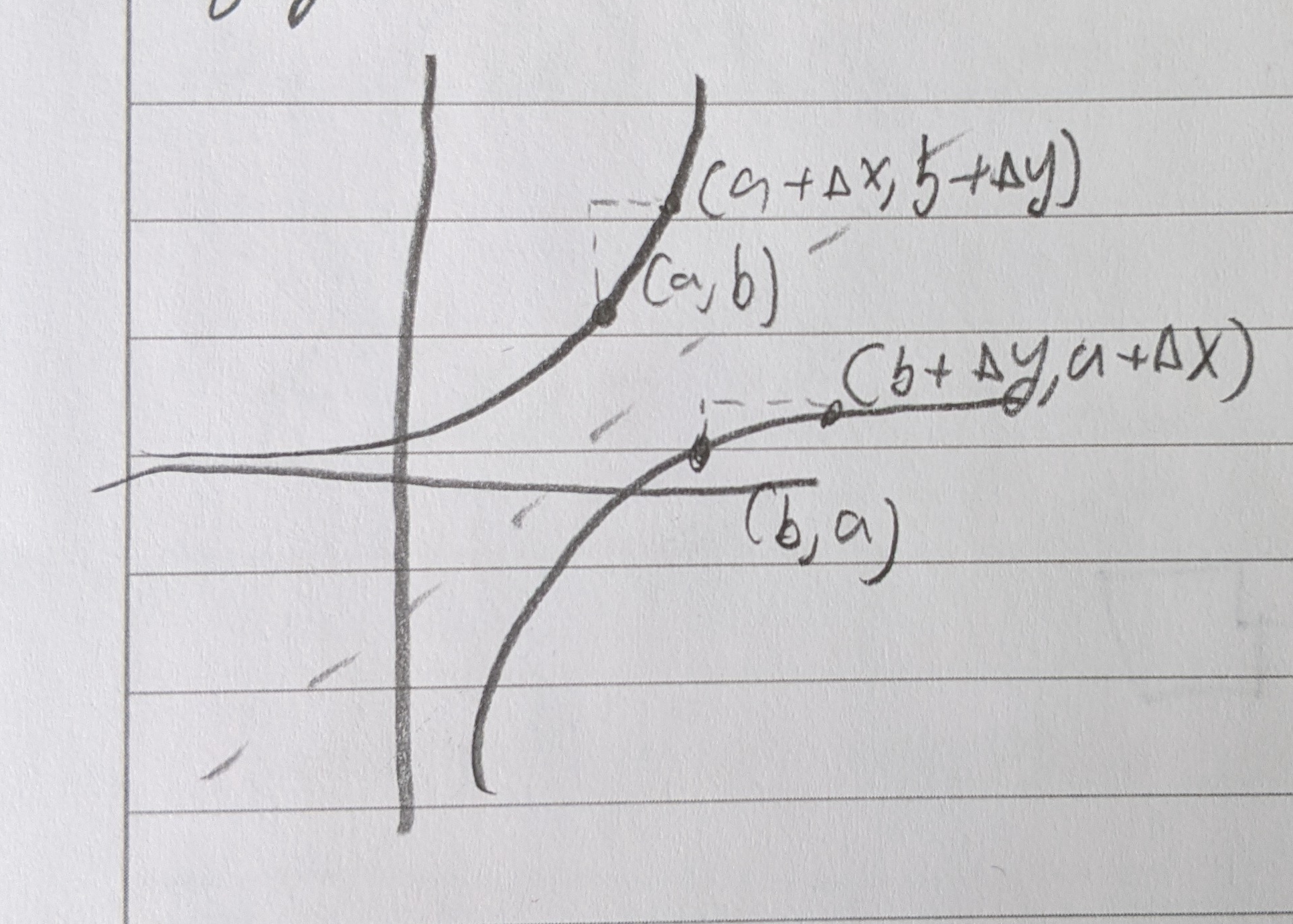
When the slope of the function is steep, the slope of the inverse is shallow and vice versa.

Example:

$y=x^{5}+x^{2}+1$

Inverse:

$x=y^5 + y^3 + 1$ (looks challenging)

Operators:

Consider $(a, b)$

For the function: $f(a) = b$

For the inverse: $f^{-1}(b)=a$

But what about the slope?

$(f^{-1}(b))’ = \frac{1}{f’(a)} = \frac{1}{f’(f^{-1}(b))}$

Analytic Approach:

$f(f^{-1}(x)) = x$

Differentiate both sides:

$f’(f^{-1}(x)) * (f^{-1}(x))’ = 1$

$(f^{-1}(x))’ = \frac{1}{f’(f^{-1}(x))}$

Example

Write the derivatives of the following in terms of $x,\ f,\ f’$

$g(x) = \frac{f(\frac{1}{x})}{x}$

$g’(x) = \frac{x*f’(\frac{1}{x}) * (\frac{-1}{x^2}) -f(\frac{1}{x})}{x^2}$

(Recall that $k(x) = f(\frac{1}{x}) = f(u)$ therefore $k’(x) = f’(u) * \frac{du}{dx}$ )

Example

$h(x) = \sqrt{f(x)^2 + 2} = (f(x)^2 + 2)^{\frac{1}{2}} $

$h’(x) = \frac{1}{2}(f(x)^2 + 2)^{\frac{-1}{2}} * 2 f(x) * f’(x)$

$h’(x) = \frac{f(x) f’(x)}{\sqrt{f(x)^2 + 2}}$

Inverse Function Theorem

$(f^{-1}(b))’ = \frac{1}{f’(a)}$

Example:

Find the slope of $f^{-1}$ for the function $f(x)=x^3 + x$ at the value $b=2$.

$f’(x) = 3x^2 + 1 > 0\ \forall x$ so it has an inverse. (It passes the horizontal line test).

$f(x) = x^3 + x = 2$

$\therefore x=2$

So our ordered pair is $(a,b) = (1,2)$

$(f^{-1}(b))’ = \frac{1}{f’(a)} = \frac{1}{4}$

Exercise:

Use the inverse function theorem to show the function and inverse have opposite concavity.

$(f^{-1}(x))’ = \frac{1}{f’(f^{-1}(x))}$

$(f^{-1}(x))’’ = \frac{-f’‘(f^{-1}(x))*(f^{-1}(x))}{f’(f^{-1}(x))^2}$

When $f$ is increasing, $f’(x) > 0$ and $f^{-1}(x) > 0$

Therefore it has the opposite sign and therefore opposite concavity.

Example:

Use the inverse function theorem to calculate $f^{-1}$ at $b$ for $f(x) = x^2 +x^4$.

$I=(0, \infty)$

$b=2$

$(f^{-1}(b))’ = \frac{1}{f’(a)}$

Find a:

$f(x) = x^2 + x^{4} = 20 \therefore x=2$ (ignoring negative numbers)

$f’(x) = 2x + 4x^3$

$f’(2) = 36$

$\therefore (f^{-1}(b))’ = \frac{1}{36}$

Example:

Consider $f(x) = x^2 - 1$

We want the slope of $f$ when $x=4$

$f’(x) = 2x$

$f’(4) = 2(4) = 8$

So on the inverse function, what is the slope at the mirrored point?

When $x=4$, $f(4) = 4^2 - 1 = 15$. Therefore the point is $(4, 15)$.

$(f^{-1}(15))’ = \frac{1}{f’(4)} = \frac{1}{8}$

Chain Rule for Implicit Differentiation

Contrast explicitly defined function such as $y=f(x)=x^3 + x$

Consider: $xy+7 = x^5+y^5$

We can still find $\frac{\Delta y}{\Delta x}$. Just go term-by-term

$\frac{dx}{dy} x + y*1 = 5x^4 + 5y^4 \frac{dy}{dx}$

$\frac{dy}{dx} (x-5y^4) = 5x^4 - y$

$\frac{dy}{dx} = \frac{5x^4-y}{x-5y^4}$

2.4 The Exponential Function

Sequence examples

Do any of these converge as $n$ approaches infinity?

$b_n = 2^n$ no

$b_n = \frac{1}{2^n}$ yes; 0

$b_n = \frac{n}{n+1}$ yes; 1

$b_n = 7 - \frac{1}{n-2}$ yes; 7

Define a polynomial of degree $n$ such that $P_n (x) = \sum_{k=0}^{n} \frac{x^k}{k!}$

$P_n (x) = \frac{x^0}{0!} + \frac{x^1}{1!} + \frac{x^2}{2!} … + \frac{x^n}{n!}$

Recall: $5! = 5 * 4 * 3 * 2 * 1 = 5*4!$

So therefore $n! = n(n-1)!$

Example

$P_0 (x) = \sum_{k=0}^{0} \frac{x^k}{k!} = \frac{x^0}{1} = 1$

$P_1 (x) = \sum_{k=0}^{1} \frac{x^k}{k!} = \frac{x^0}{0!} + \frac{x^1}{1!} = 1+x$

$P_2 (x) = \sum_{k=0}^{2} \frac{x^k}{k!} = \frac{x^0}{0!} + \frac{x^1}{1!} + \frac{x^2}{2!} = 1 + x + \frac{x^2}{2}$

Because the factorial increases faster than the exponential, the sequence converges. And we call the new function $e^x = \lim_{n \to \infty} P_n (x) = \lim_{n \to \infty} \sum_{k=0}^{n} \frac{x^k}{k!}$

What should $n$ be to get $e$ correct to 3 decimals? (2.718)

$n$ needs to be great than or equal to 6 to get 2.718…

Let’s differentiate the function:

$P_0 ‘ (x) = 1’ = 0$

$P_1 ‘ (x) = (1+x)’ = 1$

$P_2 ‘ (x) = (1 + x + \frac{x^2}{2})’ = 1 + x$

$P_3 ‘ (x) = (1 + x + \frac{x^2}{2} + \frac{x^3}{6})’ = 1 + x + \frac{x^2}{2}$

Generally for $k \ge 1$ $P_n ‘ (x) = \left( \sum_{k=0}^{n} \frac{x^k}{k!} \right)’ = \sum_{k=1}^{n} \frac{k x^{k-1}}{k!} = \sum_{k=1}^{n} \frac{x^{k-1}}{(k-1)!}$

Therefore, for $n \ge 1,\ P_n ‘ (x) = P_n(x)$

So in other words, $(e^x)’ = e^x$

Example

$y=e^{5x}$ find $y’$

$y’ = e^{5x} * 5 = 5e^{5x}$

$p(w) = 5w^3 + we^{w^2-7w}$

$p’(w) = 15w^2 + we^{w^2-7w} * (2w-7) + e^{w^2-7w} * 1$

$p’(w) = 15w^2 + w(2w-7)e^{w^2-7w} + e^{w^2-7w}$

Properties

Domain: All reals and Range: positive real
For all x, $e^x = \lim_{n \to \infty} (1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + …)$
$e^0 = 1$
$(e^x)’ = e^x$
For all $x$, $e^{-x} = \frac{1}{e^x}$
For all $x$, $e^x > 0$
$e^x$ is strictly increasing and its graph is always concave up
For all $x$ and $a$, $e^{x+a} = e^x \cdot e^a$
For all $x+\text{rational } r$, $e^{rx} = (e^x)^r$
$e\approx 2.71828182846$
$\lim_{x \to -\infty} e^x = 0$ and $\lim_{x \to \infty} e^x = \infty$
$e^x = \lim_{n \to \infty} (1+\frac{x}{n})^n$

Example

Find the critical points of $f(x) = e^x$ and the concavity and test for points of inflection.

$f’(x) = e^x$ - has no critical points

$f’‘(x) = e^x$ - has no points of inflection and is always concave up

Example

$f(x) = \frac{e^{2x} - 1}{e^x - 5}$ Find $\lim_{x \to \infty}$ and $\lim_{x \to -\infty} $ and $f’(x)$ and determine where $f$ is increasing and decreasing.

$f’(x) = \frac{(e^x+5)2e^{2x} - (e^{2x}-1)e^x}{(e^x+5)^2} = \frac{e^{3x} + 10e^{2x} + e^x}{(e^x + 5)^2}$

$\lim_{x \to \infty} f(x) = \infty$

$\lim_{x \to -\infty} f(x) = \frac{\frac{1}{\infty} - 1}{\frac{1}{\infty} + 5} = \frac{-1}{5} $

The function is always increasing because the numerator and denominator of the derivative can only be positive.

Example

Find the derivative in terms of $f’(x)$ and $f(x)$ of

$g(x) = e^{f(x)}$

$g’(x) = f’(x)e^{f(x)}$

$g(x) = e^{f(e^x)}$

$g’(x) = f’(e^x) e^{f(e^x)} e^x$

$g(x) = f(e^{\frac{1}{x}})$

$g’(x) = f’(e^{\frac{1}{x}}) e^{\frac{1}{x}} \frac{-1}{x^2}$

$g(x) = f(x)e^{x}$

$g’(x) = f(x) e^x + e^x f’(x) = e^x(f’(x) + f(x))$

2.5 The Natural Logarithm

Define the natural log $\ln$ (“base e log”, $\log_e$) as the inverse function of exp (exponential function).

Exponential Function

Domain $(\infty, \infty)$
Range $(0, \infty)$

Logarithms

Domain $(0, \infty)$
Range $(-\infty, \infty$

Properties

Domain and range are above
For all $x$ and all $y>0$, $\ln (e^x) = x$ and $e^{\ln y} = y$
$\ln (1) = 0$ and $\ln (e) = 1$

Purple: $\ln(x)$

Green: $e^x$

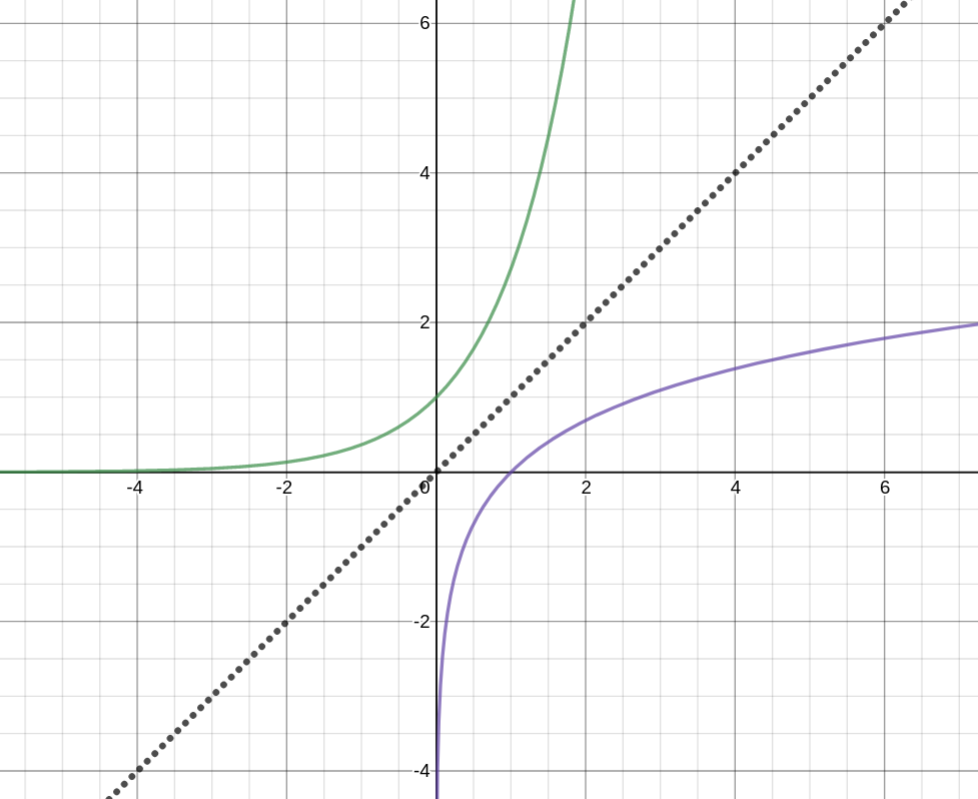
And the derivative of $\ln(x) = \frac{1}{x}$

$\lim_{x \to \infty} \ln (x) = \infty$ $\lim_{x \to 0^+} \ln (x) = -\infty$

Theorem

For $x>0$, $\ln ‘ (x) = \frac{1}{x}$ so $\ln ‘’ (x) = \left( \frac{1}{x} \right) ‘ = \frac{-1}{x^2}$

Therefore $\ln (x)$ is strictly increasing and is always concave down.

Proof by the inverse function theorem

$f(x) = e^x$

$f’(x) = \ln x$

$\frac{d}{dx}\ln x = \left( f^{-1} \right)’ (x) = \frac{1}{f’(f^{-1}(x))} = \frac{1}{f’(\ln x)}$

$f(x) = e^x$

$f’(x) = e^x$

$\frac{d}{dx} \ln x= \frac{1}{e^{\ln x}} = \frac{1}{x}$

Alternatively:

$f(x) = \ln x$

$f’(x) = e^x$

$\frac{d}{dx}e^x = \left( f^{-1} \right)’ (x) = \frac{1}{f’(f^{-1}(x))} = \frac{1}{f’(e^x)} = e^x$

$f’(x) = \frac{1}{x}$

Algebraic Properties of Logs

Consider the graphs $\ln x$ (in red) and $\ln (5x)$ (in blue)

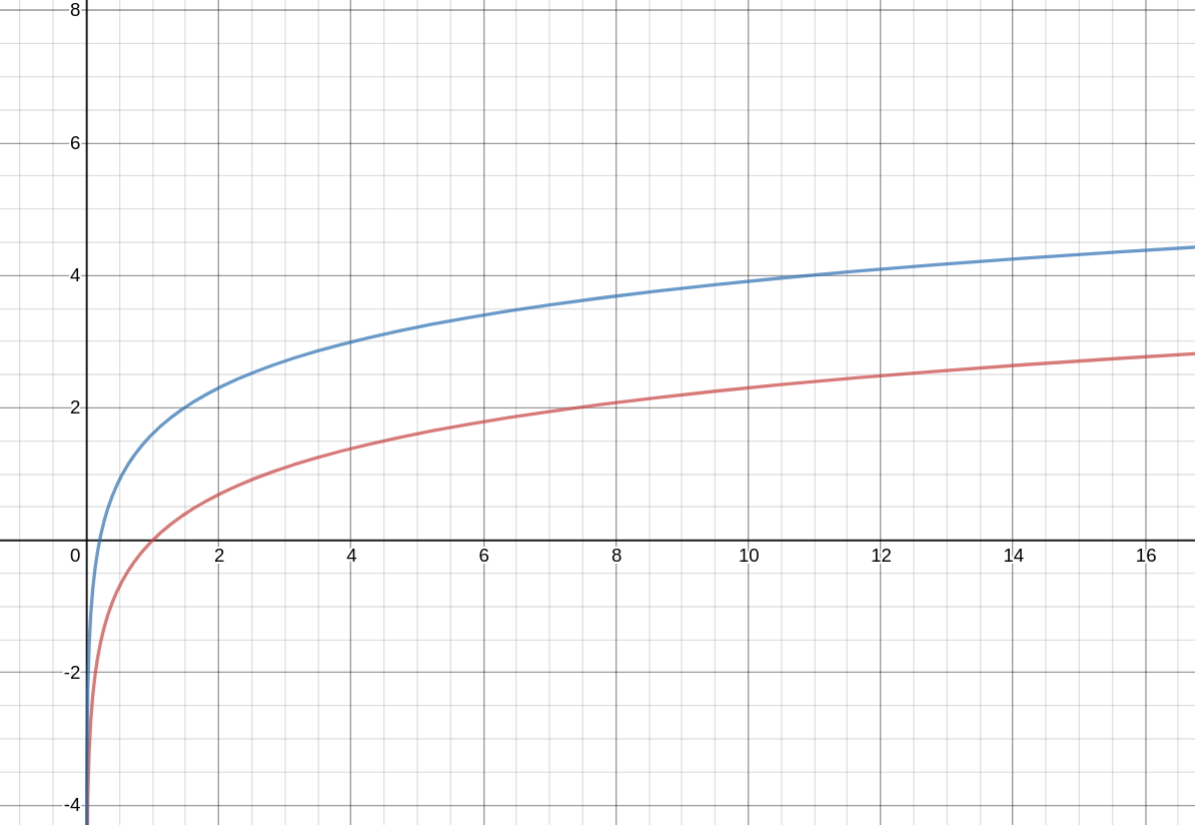
$y = f(x) = \ln x$

$f’(x) = \frac{1}{x}$

$y = g(x) = \ln 5x$

$g’(x) = \frac{1}{5x} * 5 = \frac{1}{x}$

They have the same slope

The Properties

if $x>0,\ \ln \frac{1}{x} = \ln x^{-1} = -\ln (x)$
For all $x>0$ and $a>0$, $\ln ax = \ln a + \ln x$ (NOT $(\ln a)(\ln b)$)
For all $x>0$ and $a>0$, $\ln \frac{a}{x} = \ln a - \ln x$
For $x>0$ and $r$ rational, $\ln x^r = r\ln x$

Logarithmic Differentiation

Steps:

Take logs of both sides
Differentiate both sides
Multiply both sides by $f(x)$

$f(x) = \ln (x^2 + 1)^{\frac{1}{2}} = \frac{1}{2} \ln(x^2 + 1)$

$f’(x) = \frac{1}{2} \frac{1}{x^2 + 1} 2x$

Given:

$y = f(x) = \frac{(x^2 + 1)^6 e^{5x^3-2x}}{\sqrt{x^4+7}}$

We want $f’(x)$

Recall $\ln (\frac{ab}{c}) = \ln a + \ln b - \ln c$

$\ln f(x) = 6\ln (x^2 + 1) + 5x^3 - 2x - \frac{1}{2} \ln(x^4) + 7$

$\frac{1}{f(x)} f’(x) = 6 * \frac{1}{x^2 + 1} 2x + 15x^2 - 2 - \frac{1}{2} \frac{1}{x^4 + 7} 4x^3$

$f’(x) = \frac{(x^2 + 1)^6 e^{5x^3-2x}}{(x^4 + 7)^{\frac{1}{2}}} \left( \frac{12x}{x^2 + 1} + 15x^2 - 2 - \frac{2x^3}{x^4+7} \right)$

Example

$f(x) = x^2$

$\ln(x) = 2\ln x$

$\frac{1}{f’(x)} = \frac{2}{x}$

$f’(x) = x^2 \frac{2}{x} = 2x$

Example

$y = \frac{x^5}{(1-10x)\sqrt{x^2+2}}$

$\ln y = 5\ln 5 - \ln (1-10x) - \frac{1}{2}\ln (x^2 +2)$

$\frac{1}{y} \frac{dy}{dx} = \frac{5}{x} - \frac{1}{1-10x} (-10) - \frac{1}{2} \frac{1}{x^2+2} 2x$

$\frac{dy}{dx} = \frac{x^5}{(1-10x)(\sqrt{x^2+2}} \left(\frac{5}{x} + \frac{10}{1-10x} - \frac{x}{x^2+2} \right)$

Proving Rules Using Logarithmic Differentiation

Product Rule:

Given $y=f g$ where $f$ and $g$ are differentiable at $x$ find $y’$

$\ln y = \ln (f g) = \ln f + \ln g$

$\frac{1}{y} y’ = \frac{1}{f}f’(x) + \frac{1}{g}g’(x)$

$y’ = f g (\frac{1}{f} f’(x)) + f g (\frac{1}{g}g’(x))$

$y’ = gf’(x) + fg’(x)$

Quotient Rule:

$y= \frac{f}{g}$

$\ln y = \ln f - \ln g$

$\frac{1}{y} y’(x) = \frac{1}{f}f’(x) - \frac{1}{g}g’(x)$

$y’(x) = \frac{f}{g} \frac{1}{f}f’(x) - \frac{f}{g} \frac{1}{g} g’(x)$

$y’(x) = \frac{f’(x)}{g} - \frac{f * f’(x)}{g^2}$

$y’(x) = \frac{g * f’(x)}{g^2} - \frac{f * f’(x)}{g^2}$

$y’(x) = \frac{g * f’(x) - f * f’(x)}{g^2}$

Example:

$y = \frac{\sqrt{x^2 - 11} }{x^6 \sqrt{x^2 + 5} }$

$\ln y = \frac{1}{2} \ln (x^2 - 11) - 6 \ln x - \frac{1}{2} \ln (x^2 + 5)$

$\frac{1}{y} y’ = \frac{x}{x^2 - 11} - \frac{6}{x} - \frac{1}{x^2 + 5}$

$y’ = \left( \frac{x}{x^2 - 11} - \frac{6}{x} - \frac{1}{x^2 + 5} \right) \left( \frac{\sqrt{x^2 -11} }{x^6 \sqrt{x^2 + 5} } \right)$

2.6 General Exponential and Logarithmic Functions

Define base $b$ exponential function $b^x$

$b^x = e^{x \ln b}$

Domain: $(-\infty, \infty)$ Range: $(0, \infty)$

Properties:

$a,\ b > 0,\ x, y \text{Real}$

$b^0 = 1$
$b^{x+y} = b^x * b^y$
$b^{-x} = \frac{1}{x^x}$
$(b^x)^y = b^{xy}$
$\ln b^x = x \ln b$
$a^x * b^x = (ab)^x$

Derivative for $b>0$

$(b^x)’ = (e^{x \ln b})’ = e^{x \ln b} * \ln b = b^x \ln b$

Example

Find the slope of $f(x) = 2^x$ at $x=-2$, $x=2$.

$f’(x) = 2^x \ln 2$

$f’(-2) = \frac{1}{4} \ln 2 \approx 0.017$

$f’(2) = 4 \ln 2 \approx 2.77$

Example:

$(\ln (3^t + 1))’$

$= \frac{3^t \ln 3}{3^t + 1}$

Example:

For $f(x) = x * 2^x$ find $f’(x)$, intervals of increasing and decreasing, and extreme values.

$f’(x) = 2^x + x 2^x \ln 2$

$f’(x) = 2^x (1 + x \ln 2) = 0$

$\therefore x = \frac{-1}{\ln 2} \approx -1.44$

Intervals:

$(-\infty, \frac{-1}{\ln 2}) : f’(-2) = 2^{-2} (-2 \ln 2 + 1) < 0$ Decreasing
$(\frac{-1}{\ln 2}, \infty) : f’(0) = 1+0 > 0$ Increasing

Therefore $x= \frac{-1}{\ln 2}$ is a global min.

$f(\frac{-1}{\ln 2}) = \frac{-1}{\ln 2} 2^{\frac{-1}{\ln 2}}$

$f(\frac{-1}{\ln 2}) = \frac{-1}{\ln 2} \frac{1}{e}$

$f(\frac{-1}{\ln 2}) = \frac{-1}{\ln 2 * e}$

Second Derivative

$(b^x)’’ = (b^x \ln b)’ = \ln b (b^x \ln b) = (\ln b)^2 b^x$

For $b>0$:

If $b=1$, $b^x = 1^x = 1$
If $b>1$, $b^x$ is strictly increasing and its graph is always concave up.
If $b<1$, $b^x$ is strictly decreasing an its graph is always concave up.

Example:

Radioactive Decay

$\frac{dA}{dt} = -k A$

$A(t) = A_o e^{-k t}$

When $t=t_{\frac{1}{2}}$

$A(t_{\frac{1}{2}}) = \frac{1}{2} A_o = \frac{A_o}{2} = A_o e^{-k t_{\frac{1}{2}}}$

$\ln (\frac{1}{2}) = \ln e^{-k t_{\frac{1}{2}}} = -k t_{\frac{1}{2}}$

$k = \frac{-\ln \frac{1}{2}}{t_{\frac{1}{2}}} $

$A(t) = A_o e^{\frac{-\ln 2 t}{t_{\frac{1}{2}}}}$

$A(t) = A_o e^{\ln 2^{-1} * \frac{t}{t_{0.5}}}$

$A(t) = A_o \left( \frac{1}{2} \right)^{\frac{t}{t_{0.5}}}$

Define the base $b$ log, $\log_{b}$ is the inverse function of $b^x$. So for all $x>0$, $b^{\log_b x} = x$ and for all $y$, $\log_b b^{y} = y$

Converting to Base e

$\log_b x = \frac{\ln x}{\ln b}$

Check $\log_{10} 100 = \frac{\ln 100}{\ln 10} = \frac{2\ln 10}{\ln 10} = 2$

Derivatives of Other Bases

$(\log_{b}{x})’ = \frac{1}{\ln} \frac{1}{x} = \frac{1}{x \ln b}$

Example:

$(\log_{10}(x^2 + 1))’ = \frac{1}{\ln 10} \frac{1}{x^2+1} * 2x = \frac{2x}{\ln 10 (x^2 + 1)}$

General Power Rule

$\left( x^p \right) ‘ = px^{p-1}$

Proof: $(x^p)’ = (e^{p \ln x})’ = e^{p \ln x} \frac{p}{x} = x^p \frac{p}{x} = px^{p-1}$

Example: (“General Power Exponential Rule”)

Find the derivative of $g(x)^{f(x)}$

$(g(x)^{f(x)})’ = e^{f(x) * \ln g(x)} = e^{f \ln g} (f * \frac{1}{g} g’(x) + \ln g * f’(x)) = g^{f-1} f g’(x) + g^f (\ln g) (f’(x))$

Example (#7):

$f(x) = (\log_{3}{x})^2$

$f’(x) = 2 (\log_{3} x) * \frac{1}{x \ln 3} = \frac{2 \log_{3} x}{x \ln 3}$

$f(x) = \left( \frac{\ln x}{\ln 3} \right) ^2 = \frac{1}{(\ln 3) ^2} (\ln x)^2$

$f’(x) = \frac{1}{(\ln 3)^2} 2 \ln x \frac{1}{x} = \frac{2 \ln x}{x (\ln 3)^2} = \frac{2}{x \ln 3} \frac{\ln x}{\ln 3} = \frac{2 \log_{3} x}{x\ln 3}$

Example (#21):

Find intervals of increasing and decreasing and critical points for $f(x) = (x^2)^x$.

$f’(x) = \ln f(x) = \ln (x^2)^x = x \ln (x^2)$

$\frac{1}{f} f’(x) = x \frac{1}{x^2} 2x + \ln x^2 * 1$

$f’(x) = (x^2)^x (2 + \ln x^2)$

Critical points are $x=0$ and $2+\ln x^2 = 0$

$x^2 = \frac{1}{e^2}$

$x = \pm \frac{1}{e}$ are other critical points

Example (#16):

$p(x) = 12^{x \ln x} = e^{\ln 12^{x \ln x}} = e^{x \ln x \ln 12}$

$p’(x) = e^{x \ln x \ln 12} * \ln 12 (x \frac{1}{x} + \ln x * 1) = 12^{x \ln x} \ln 12 (1+ \ln x)$

NOTE: $x^{x \ln 12} = 12^{x \ln x}$

2.7 Trig Functions: Sine and Cosine

$f(x) = f(x-p) = f(x+p)$

$p>0$ and $p$ is the period of the function.

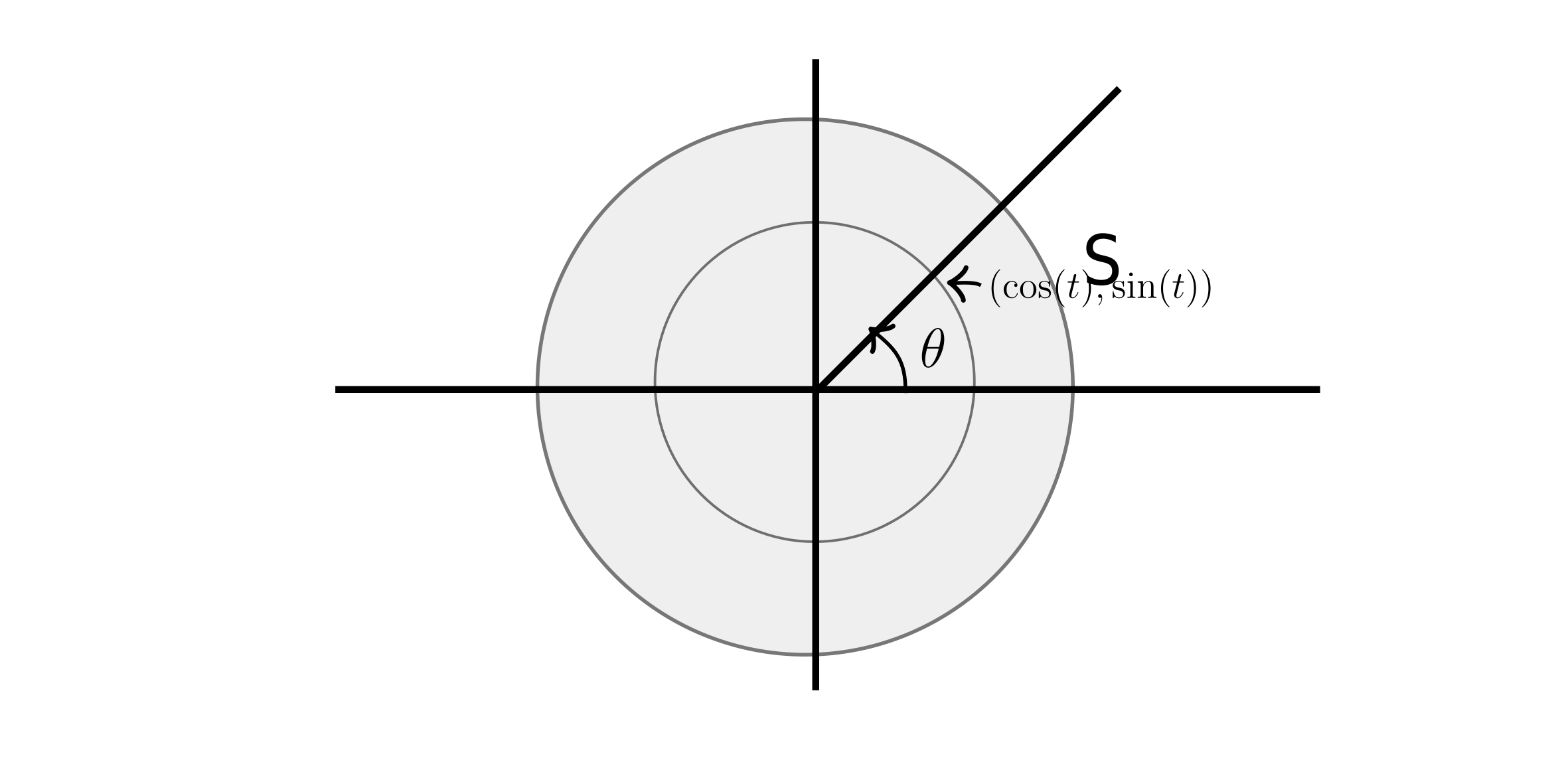
$s = r \theta$

Where the radius of the circle is $r$

By similarity angle $\theta = \frac{s}{r} = \frac{t}{1}$

$C = 2\pi r$

Properties

For all $t$, $\sin ^2 t + \cos ^2 t = 1$
sine + cosine are periodic with a period of $2\pi$ and for integers $k$, $\sin t = \sin (t + 2\pi k)$ and $\cos t = \cos (t + 2\pi k)$
$\sin (-t) = - \sin t$ (odd function ) and $\cos (-t) = \cos t$ (even function)
Angle addition $\sin (\alpha + \beta) = \sin (\alpha) \cos (\beta) + \sin(\beta) \cos (\alpha)$ and $\cos (\alpha + \beta) = \cos (\alpha) \cos (\beta) - \sin (\alpha) \sin (\beta)$
Double angles: $\sin (2 \alpha) = 2 \sin(\alpha) \cos (\alpha)$ and $\cos (2 \alpha) = 2 \cos^2 (\alpha) - \sin ^2 (\alpha) = 2 \cos ^2 (\alpha) - 1 = 1 - 2 \sin ^2 (\alpha)$
For all $\alpha$, $\sin (\alpha) = \cos (\frac{\pi}{2} - \alpha)$ and $\cos (\alpha) = \sin (\frac{\pi}{2} - \alpha)$

$\sin(t)$

$t=0: 0$
$t=\frac{\pi}{6}: \frac{1}{2} $
$t=\frac{\pi}{4}: \frac{\sqrt{2} }{2}$
$t=\frac{\pi}{3}: \frac{\sqrt{3} }{2}$
$t=\frac{\pi}{2}: 1$

$\cos(t)$

$t=0: 1$
$t=\frac{\pi}{6}: \frac{\sqrt{3}}{2} $
$t=\frac{\pi}{4}: \frac{\sqrt{2}}{2}$
$t=\frac{\pi}{3}: \frac{1}{2}$
$t=\frac{\pi}{2}: 0$

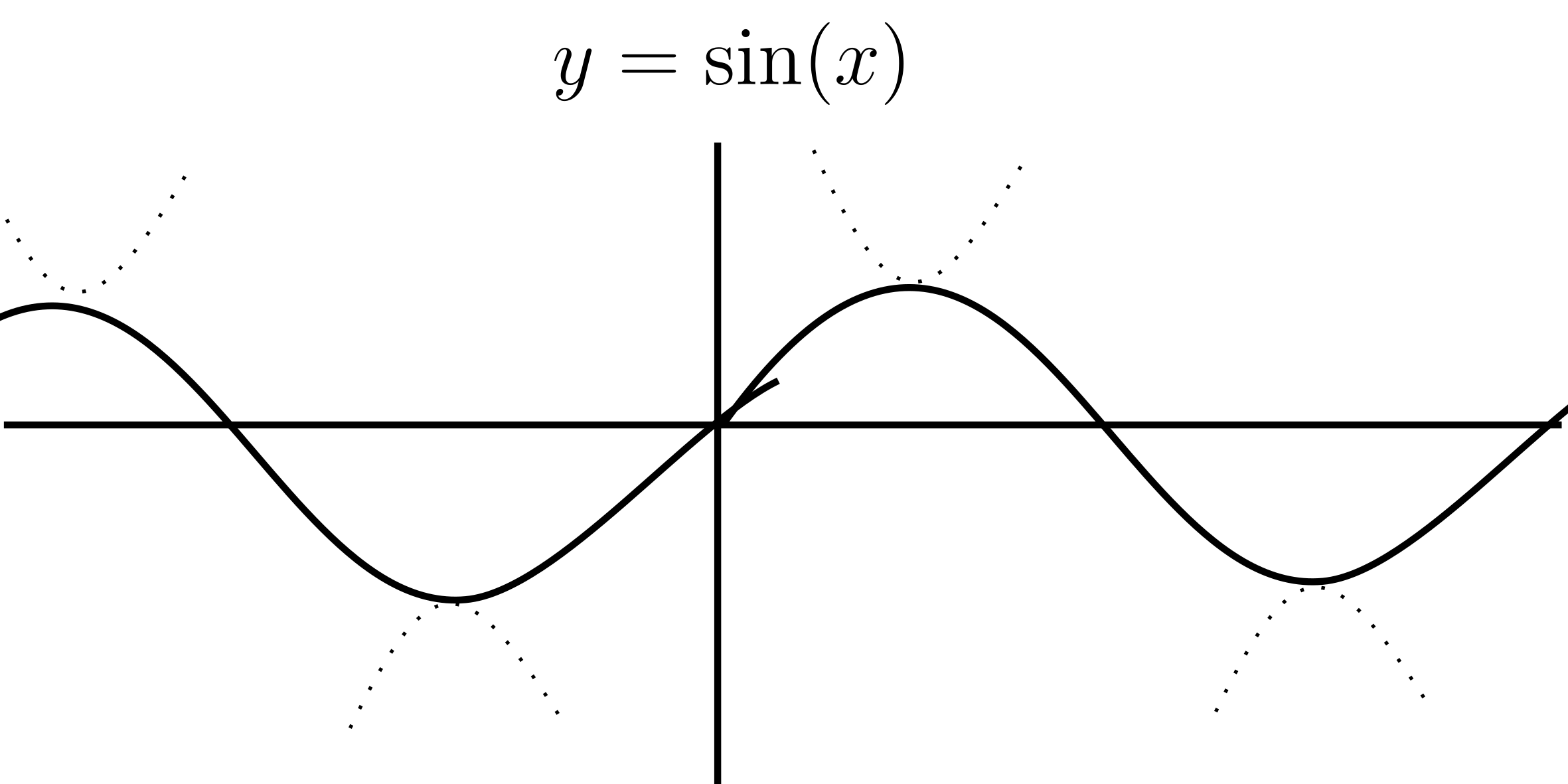
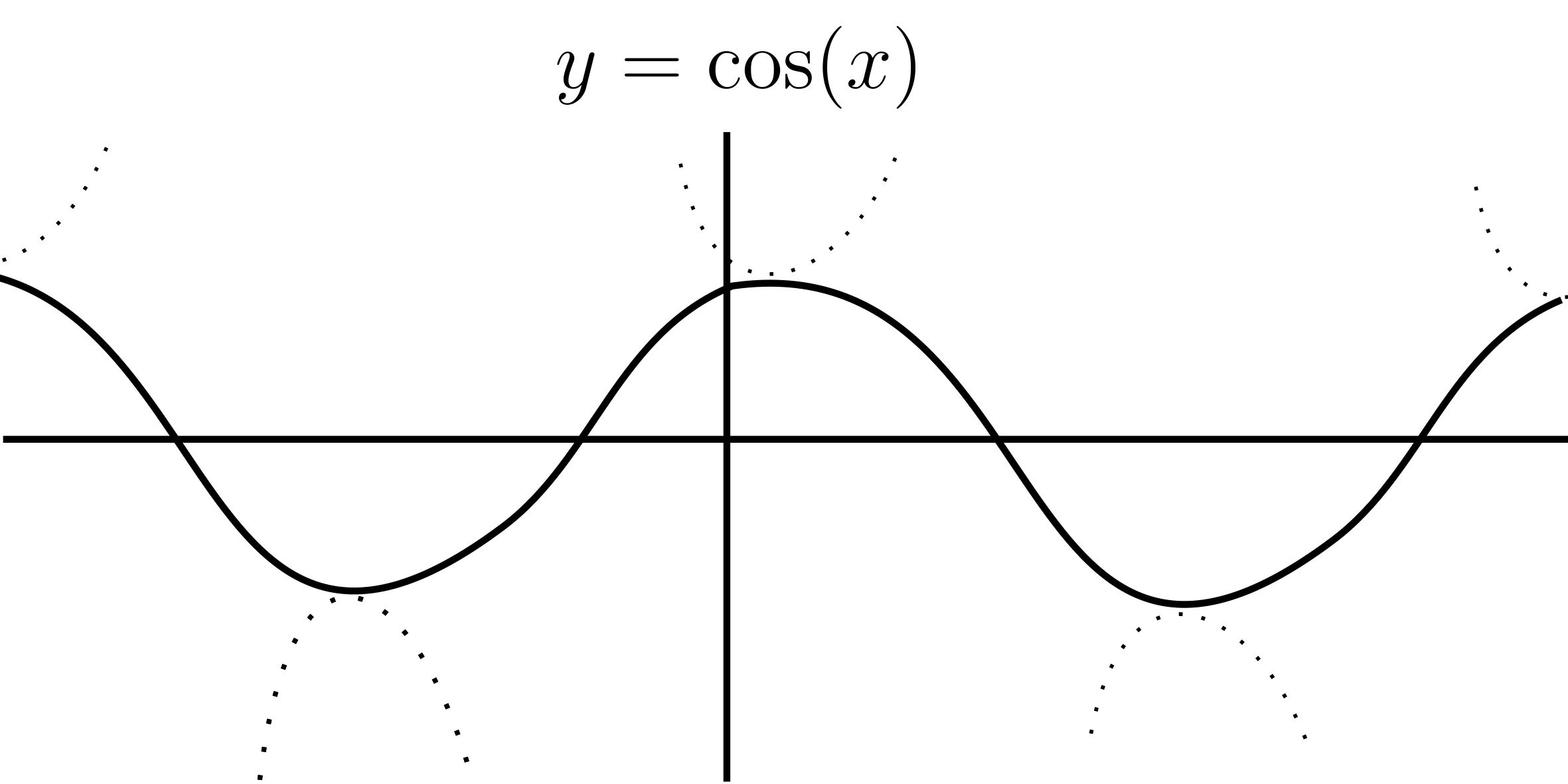
$y=\sin (x)$

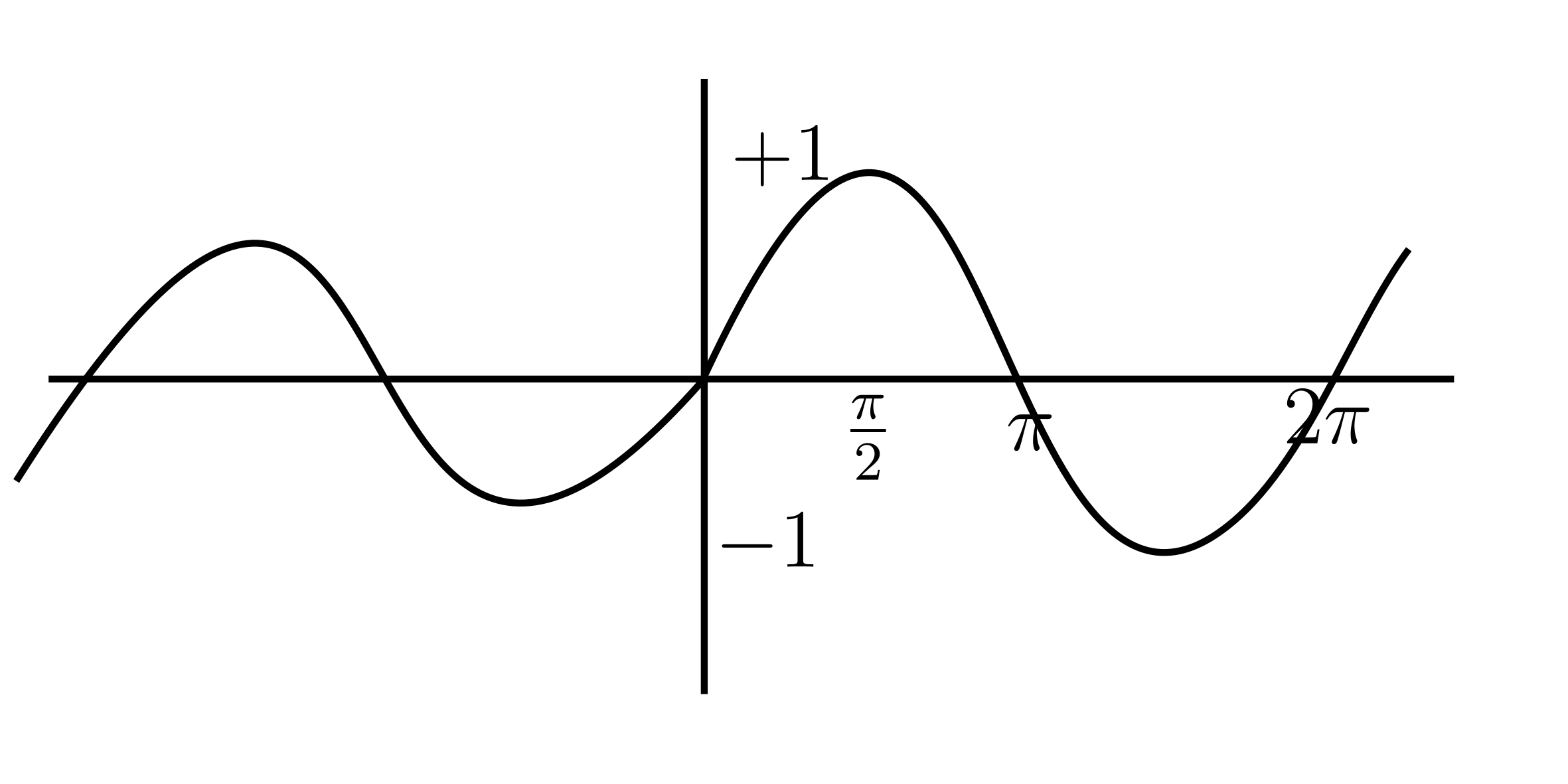
$y=\cos (x)$

Theorem

Derivatives

$\sin’(x) = \cos(x)$
$\cos’(x) = -\sin(x)$

Second Derivatives

$\sin’‘(x) = - \sin(x)$
$\cos’‘(x) = -\cos(x)$

Consider the 2nd order differential equation

$y’’ + y = 0$

Has salutations $y=\sin(x)$ and $y=\cos(x)$

Example:

$z= r \sin (5r)$

Find $\frac{dz}{dr}$

$= 5r \cos(5r) + \sin(5r)$

Example:

$w_1 = e^{\cos (u^2)}$

Find $\frac{dw_1}{du}$

$=-\sin(u^2) 2u e^{\cos(u^2)}$

Example:

$w_2 = e^{\cos ^2 (4u)}$

Find $\frac{dw_2}{du}$

$=e^{\cos^2 (4u)} 2 \cos (4u) (-\sin(4u) 4$

Example:

Calculate $(\ln \cos (3x))’$

$= \frac{1}{\cos (3x)} -\sin (3x) 3$

Example:

Calculate $(5 \cos (2x) + \frac{\sin x^2}{x})’$

$= 5 -\sin (2x) 2 + \frac{x \cos (x^2) 2x - \sin (x^2)}{x^2}$

Example: Simple Harmonic Oscillator

At $t$ seconds, the position of the block is $x=2\cos(3t)$

Find:

$x$, $v$, and $a$ of the block at $t=0$ and $t=\frac{\pi}{2}$s
When will the block return to where it started?
When will it reach maximum displacement?
What happens after a long time?

$x=2 \cos(3t)$

$v=-6\sin(3t)$

$a=-18 \cos(3t)$

It returns when $3t = 2\pi$, therefore $t= \frac{2\pi}{3}$

It reaches maximum displacement when the derivative is zero. So when $v=-6 \sin(3t)$ is 0:

$\sin 3t = 0$

$3t = k \pi$ where $k$ is an integer.

For even: $2k$

For odd: $2k+1$

So $t= \frac{k\pi}{3}$

When $k=1$, $x = 2 \cos (3 * \frac{1 \pi}{3}) = -2$

When $k=2$, $x = 2\cos (3 * \frac{2\pi}{3}) = + 2$

So after a long time, it goes between -2 and +2.

Example: Damped Harmonic Oscillator:

Friction adds: $x= 2 e^{-t} \cos(3t)$

As $t \to \infty$, $x$ approaches 0.

Find $x,\ v,\ a$ at $t=0,\ \frac{\pi}{2}$

Solutions of Differential Equations

Suppose $f’’(\omega) = -\omega ^ 2 f$

Let $a=f(0)$ and $b=f’(0)$

Then $f(x) = a \cos (\omega x) + \frac{b}{\omega} \sin(\omega x)$

Example: Hooke’s Law

$f= -kx = ma$

$mx’’ = -kx$

$x’’= \frac{-k}{mx}$

$x’’ = -\left( \sqrt{\frac{k}{m}} \right) ^2 x$

$w = \sqrt{\frac{k}{m}}$

The equation has solutions:

$x = c_1 \cos (\omega t) + c_2 \sin (\omega t)$

$c_1 = a = x(0) = 2m$

$c_2 = b = \frac{x’(0)}{\omega} = 0$

Therefore $x = 2\cos(3t)$

Note (from previous class):

$12^{x\ln x} = x^{x\ln 12}$

Prove that $12^{2 \ln(2)} = 2^{2 \ln 12}$ can prove $3^{\ln 4} = 4^{\ln 3}$

$(4 * 3)^{2\ln 2} = 2^{2\ln (4 * 3)}$

$4^{2\ln 2} * 3^{2 \ln 2} = 2^{2\ln (4)+ 2\ln(3)}$

$2^{2*2\ln 2} * 3^{2\ln 2} = 2^{2\ln4} * 2^{2\ln3}$

$2^{2\ln 4} * 3^{2\ln 2} = 2^{2 \ln 4} 2^{2\ln 3}$

$3^{2\ln 2} = 2^{2\ln 3}$

$\fbox{$3^{\ln 4} = 4^{\ln 3}$}$

$\ln(4) \ln(3) = \ln(3) \ln(4)$

2.8 The Other Trig Functions

The other trig functions are tan, cot, sec, and csc.

Because these are all quotients, we need to know when the denominator is equal to zero.

$\sin x = 0$ at $x=k\pi$

$\cos x = 0$ at $x=\frac{\pi}{2} + k\pi$ or $(2k+1)\frac{\pi}{2}$

$\tan (x) = \frac{\sin (x)}{\cos (x)}$, $x \neq \frac{\pi}{2} + k \pi$

$\cot (x) = \frac{\cos (x)}{\sin (x)}$, $x \neq k\pi$

$\sec (x) = \frac{1}{\cos (x)}$, $x \neq \frac{\pi}{2} + k\pi$

$\csc (x) = \frac{1}{\sin (x)}$, $x \neq k\pi$

$\sin ^2 (x) + \cos ^2 (x) = 1$

Divide by $\cos ^2 (x)$:

$\tan^2 (x) + 1 = \sec ^2 (x)$

Divide by $\sin ^2 (x)$ :

$1 + \cot ^2 (x) = \csc ^2 (x)$

Properties

Two angles are complementary if $\alpha + \beta = \frac{\pi}{2}$.

If $\alpha + \beta$ are complementary, $\sin (\alpha) = \cos (\beta)$

So $\text{trig function}(\alpha) = \text{co-trig function}(\beta)$

Examples:

$\tan (\alpha) = \cot (\beta)$

$\sec (\alpha) = \csc (\beta)$

Because

$\sin (x \pm \pi) = - \sin (x)$

$\cos (x \pm \pi) = - \cos (x)$

So, $\tan (x) + \cot (x)$ will be period with period $\pi$

$\cos (x)$ is even

$\sin (x)$ is odd

$\tan(x)$ and $\cot(x)$ are both odd.

The dotted function is the inverse:

$\sec (x)$ is even

$\csc (x)$ is odd

Because they are reciprocals and

$\mid \sin (x) \mid \le 1$ then $\mid \csc (x) \mid \ge 1$ reflected about $x= + \frac{\pi}{2}$, $y=1$
$\mid \cos (x) \mid \le 1$ then $\mid \sec (x) \mid \ge 1 $ reflected about $x=0$, $y=1$

The dotted function is the inverse and the asymptotes are when the regular function are at 0:

We said that the tangent function is always increasing.

Example:

So what is the derivative of $\tan (x)$?

$\tan (x)’ = \left(\frac{\sin(x)}{\cos(x)}\right)’ = \frac{\cos(x) * \cos(x) - \sin(x) * -\sin (x)}{\cos (x)^2}$

$\tan(x)’ = \frac{(\cos(x) + \sin(x))^2}{\cos (x)^2} = \frac{1}{\cos (x)^2}$

Example:

Find $\frac{d}{dx} (\cot (x))$

$\cot (x)’ = - \frac{1}{\sin(x)^2}$

Example:

Find $\frac{d}{dx} (\sec (x))$

$\sec(x)’ = \tan(x) \sec(x)$

Example:

A light house is rotating counter clockwise and completes one revolution in 8 seconds.

How fast must the child (represented by the square) run to keep up with the beam at distance $x=0.5$ miles (between the dotted line and the square in the x direction)?

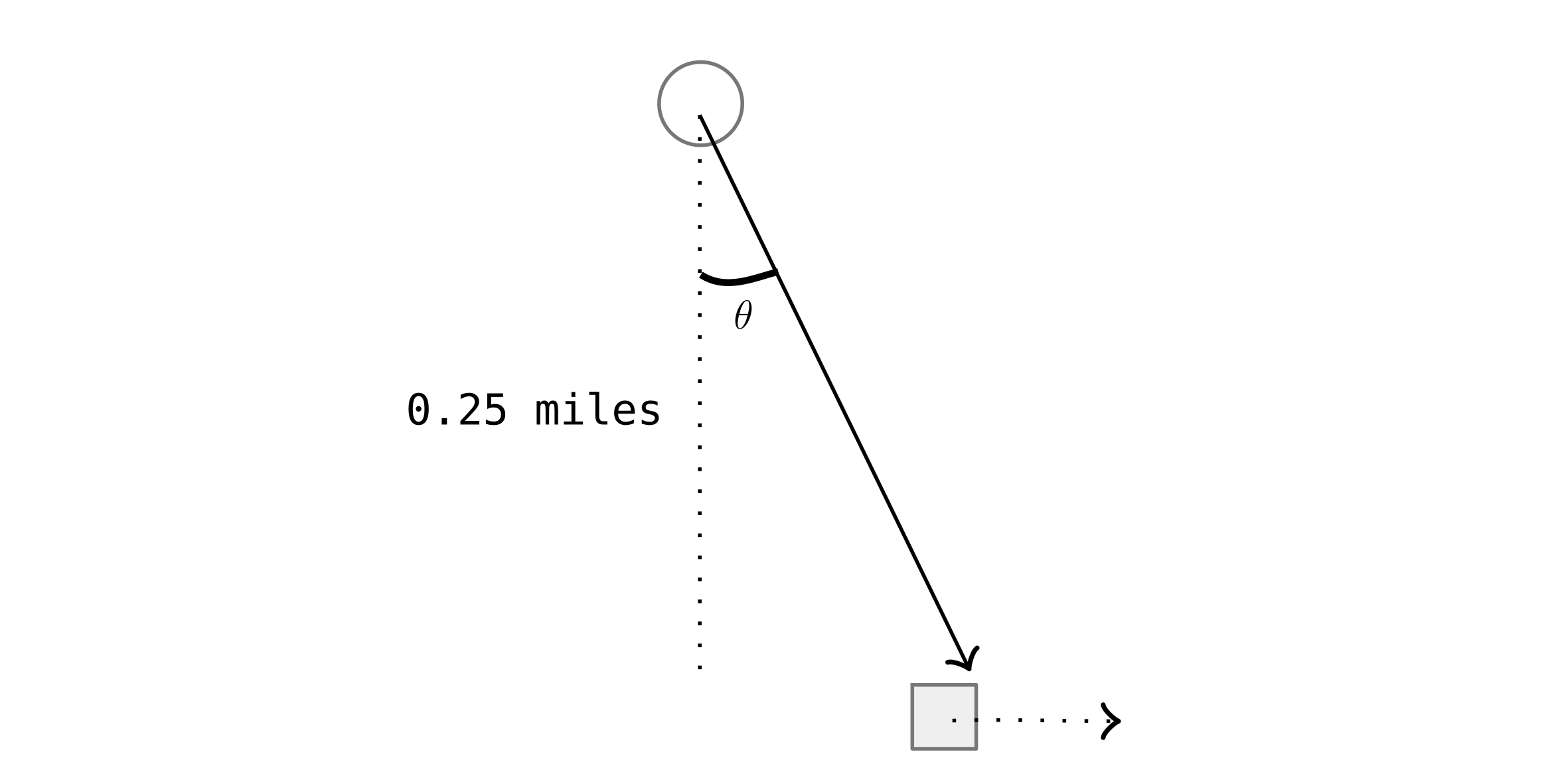
$\tan (\theta) = \frac{x}{0.25}$

$x=0.25 \tan (\theta)$

We want $\frac{dx}{dt}\mid _{x=0.25}$

$\frac{dx}{dt} = 0.25 \frac{d}{d\theta}(\tan(\theta)) \frac{dy}{dt}$

$\frac{d\theta}{dt} = \frac{2\pi}{8}$

$\frac{dx}{dt} = 0.25 \sec(\theta)^2$

When $x=0.5$ miles, what is $\sec(\theta)^2$?

Recall $\tan(\theta)^2 + 1 = \sec(\theta)^2$

$x=0.25 \tan(\theta)$

$\frac{0.5}{0.25} = \tan(\theta)$

$2^2 = \tan(\theta)^2$

$\therefore 2^2 +1 = \tan(\theta)^2 + 1 = \sec(\theta)^2$

$\frac{dx}{dt} = \frac{1}{4} 5 \frac{\pi}{4} \approx 0.9817$ miles/second

Practice:

Find the critical points to tan, cot, sec, csc.

Appendix A

Parameterized Curves and Motion

Consider the motion of a particle in the x-y plane (the dot in the middle is the foci)

NOTE: This fails to be a function (fails the vertical line test)

Create:

$x=x(t) = 2t-1$ ($t$ is the parameter)

$y=y(t) = (2t-1)^2$

By inspection $y=x^2$

Example:

Particle in the x-y plane. At $t$ seconds, $x=x(t)=1-t^2$ and $y=y(t) = t^4 +2$.

Where is the particle at $t=0,\ 1,\ 2$
Can we describe the particle’s path in terms of $x$ and $y$ (not $t$) (NOTE: We often don’t do this)
Direction of motion?
Average rate of change of $x$ and $y$ coordinates with respect to time between $t=0$ and $t=2$
$v$, speed, $a$?
x-components of $v$, $a$ at $t=2$?
Slope of tangent to the path at $t=2$?
Position: $x(t),\ y(t) = 1-t^2,\ t^4+2$

$x(0),\ y(0) = 1,\ 2$

$x(1),\ y(1) = 0,\ 3$

$x(2),\ y(2) = -3,\ 18$

Try:

$(t^2)^2 = (1-x)^2 = t^4$

$y= (1-x)^2 + 2$

$y= 1-2x+x^2 + 2$

$y= x^2 -2x +3$

As $t$ increases, $x$ decreases and $y$ increases (up and to the left).

$\frac{\Delta x}{\Delta t} = \frac{x(2) - x(0)}{2-0} = \frac{-3-1}{2} = \frac{-4}{2} = -2$

$\frac{\Delta y}{\Delta t} = \frac{y(2) - y(0)}{2-0} = \frac{18-2}{2} = \frac{16}{2} = 8$

$\vec{v} (t) = \vec{p}’(t) = (x’(t), y’(t)) = (\frac{dx}{dt}, \frac{dy}{dt}) = (-2t, 4t^3)$ (Component notation)

$\vec{a}(t) = \vec{v} ‘ (t) = (-2, 12t^2)$

Recall that speed is the vector sum of the velocity’s components.

Speed = $\mid \vec{t} \mid = \sqrt{v_x ^2 + v_y ^2} = \sqrt{(-2 t)^2 + (4t^3)^2} $

Speed = $\sqrt{4t^2 + 16t^6} = \sqrt{4t^2(1+4t^4)} = 2t \sqrt{1+4t^4}$

Speed $\mid _{t=2} = 2(2) \sqrt{1+4(2)^4} = 4 \sqrt{65}$

$v_x\mid _{t=2} = -2(2) = -4$

$a_x \mid _{t=2} = -2$

We want $\frac{\frac{dy}{dt}}{\frac{dx}{dt}} = \frac{4t^3}{-2t}$

$\frac{dy}{dx} \mid _{t=2} = \frac{4 (2)^3}{-2(2)} = -8$

Recall $y=x^2 - 2x + 3$ so $\frac{dy}{dx} \mid _{t=2} = 2x - 2 = 2(-3) - 2 = -8$ (When $t=3$, $x=-3$)

Example (#14):

$\vec{\beta} (t) = (t, t, t^2)$ find $\frac{dz}{dx}$, $Q(1, 1, 1)$

$\frac{dz}{dx} = \frac{\frac{dz}{dt}}{\frac{dx}{dt}} = \frac{2t}{1} = 2t\mid _{Q=(1, 1, 1)} = 2(1) = 2$

Example (#15):

$\vec{g}(t) = (t^3 + 2, t^3 - 3, t^3 + 17)$, find $\frac{dy}{dx}$, $Q=(10, 3, 25)$

$\frac{dy}{dx} = \frac{\frac{dy}{dt}}{\frac{dx}{dt}} = \frac{3t^2}{3t^2} = 1$

Practice:

(On your graphing calculator)

$x_1 = 2 \cos(11t)$

$y_1 = \sin (12 t)$

$x_2 = 1.5 \cos(5) - \cos (15t)$

$y_2 = 1.5 \sin (t) - \sin(15t)$

(Results in a flowery graph)

2.9 Inverse Trig Functions

Trig functions fail the horizontal line test. Therefore, we need to restrict their domains when we get their inverse.

Define:

$\sin(x)$:

Domain: $[\frac{-\pi}{2}, \frac{\pi}{2}]$
Range: $[-1, 1]$

The inverse flips the domain and range (because we reflect it across $y=x$):

$y=\sin ^-1 (x)$:

Domain: $[-1, 1]$
Range: $[\frac{-\pi}{2}, \frac{\pi}{2}]$

“y is angle whose sine is x”

$\sin(y) = \sin(\sin ^-1 (x)) = x$

Consider $y=\sin(x)$, $\frac{-\pi}{2} \le x \le \frac{\pi}{2}$

$\sin ^-1 (y) = \sin ^-1 (\sin (x)) = x$

So $y=\sin (x)$ and $x = \sin ^-1 (y)$ are equivalent if $\frac{-\pi}{2} \le x \le \frac{\pi}{2}$

So $\sin ^-1 (\sin (x)) = x$ if $\frac{-\pi}{2} \le x \le \frac{\pi}{2}$

What about $\sin (\sin ^-1 (x)) = x$ if $-1 \le x \le 1$

Find $\sin ^-1 (\frac{-1}{\sqrt{2} }) = \frac{-\pi}{4}$

Recall $\sin ^-1 (1) = \frac{\pi}{2}$

$\sin \frac{\pi}{2} = 1$

$y= \cos ^-1 (x)$

Domain from -1 to 1

$y=\tan ^-1 (x)$

Range from $\frac{-\pi}{2}$ to $\frac{\pi}{2}$

$y=\cot^-1(x)$

Intercepts the y axis at $\frac{\pi}{2}$
Range from 0 to $\pi$

$y=\sec ^-1 (x)$

Asymptotic at $\frac{\pi}{2}$
Range from 0 to $\pi$

$y=csc ^-1 (x)$

Asymptotic at -1 and 1

Domains:

So $\sin (\sin ^-1 (x)) = x$ for $-1 \le x\le 1$

So $\sin ^-1 (x)$ is the inverse of $\sin (x)$ for $\frac{\pi}{2} \le x \le \frac{\pi}{2}$

So $\cos^-1 (x)$ is the inverse of $\cos(x)$ for $0 \le x \le \pi$

So $\tan^-1 (x)$ is the inverse of $\tan(x)$ for $\frac{\pi}{2} < x < \frac{\pi}{2}$

So $\cot^-1 (x)$ is the inverse of $\cot(x)$ for $0 < x < \pi$

So $\sec^-1 (x)$ is the inverse of $\sec(x)$ for $0 \le x < \frac{\pi}{2}$, $\frac{\pi}{2} \le x < 0$

So $\csc^-1 (x)$ is the inverse of $\csc(x)$ for $0 \le x < \frac{\pi}{2}$, $0 < x \le \frac{\pi}{2}$

Derivatives

$y=\sin ^-1(x)$ we want $\frac{dy}{dx}$

$\sin (y) = \sin (\sin ^-1 (x)) = x$ for $-1 \le x\le 1$

$\cos(y) \frac{dy}{dx} = 1$

$\frac{dy}{dx} = \frac{1}{\cos (y)} = \frac{1}{\cos (\sin ^-1 (x))}$

Recall $\cos ^2 (y) = 1 - \sin ^2 (y)$

$\cos (y) = \pm \sqrt{1-\sin^2 (y)} $

$\cos (\sin ^-1 (x)) = \pm \sqrt{1-\sin^2 (\sin ^-1 x)} = \pm \sqrt{1-x^2} = \sqrt{1-x^2} $

$\therefore \frac{d}{dx}(\sin ^-1 (x)) = \frac{1}{\sqrt{1-x^2}}$

Why we can drop the plus-or-minus:

For $-x \le x\le 1$

Operate by applying $\sin ^-1$

$\sin ^-1 (-1) \le \sin ^-1 (x) \le \sin ^ -1(1)$

$\frac{-\pi}{2} \le \sin ^-1 (x) \le \frac{\pi}{2}$

If we do the same thing for $\cos ^-1(x)$:

$\frac{d}{dx} cos ^-1(x) = \frac{-1}{\sqrt{1-x^2}}$

Consider $y=\tan ^-1 (x)$, what is $\frac{dy}{dx}$

$\tan (y) = \tan (\tan ^-1 (x)) = x$

$\sec ^2 (y) \frac{dy}{dx} = 1$

$(1+\tan ^2 (y)) \frac{dy}{dx} = 1$

$(1+\tan ^2 (\tan ^-1 (x))) \frac{dy}{dx} = 1$

$(1+x^2) \frac{dy}{dx} = 1$

$\frac{dy}{dx} = \frac{1}{1+x^2} = (\tan ^-1 (x)) ‘$

$(\cot ^ -1 (x))’ = \frac{-1}{1+x^2}$

$(\sec ^-1 (x))’ = \frac{1}{\mid x\mid \sqrt{x^2 - 1}}$

$(\csc ^-1 (x))’ = \frac{-1}{\mid x\mid \sqrt{x^2 - 1}}$

Practice:

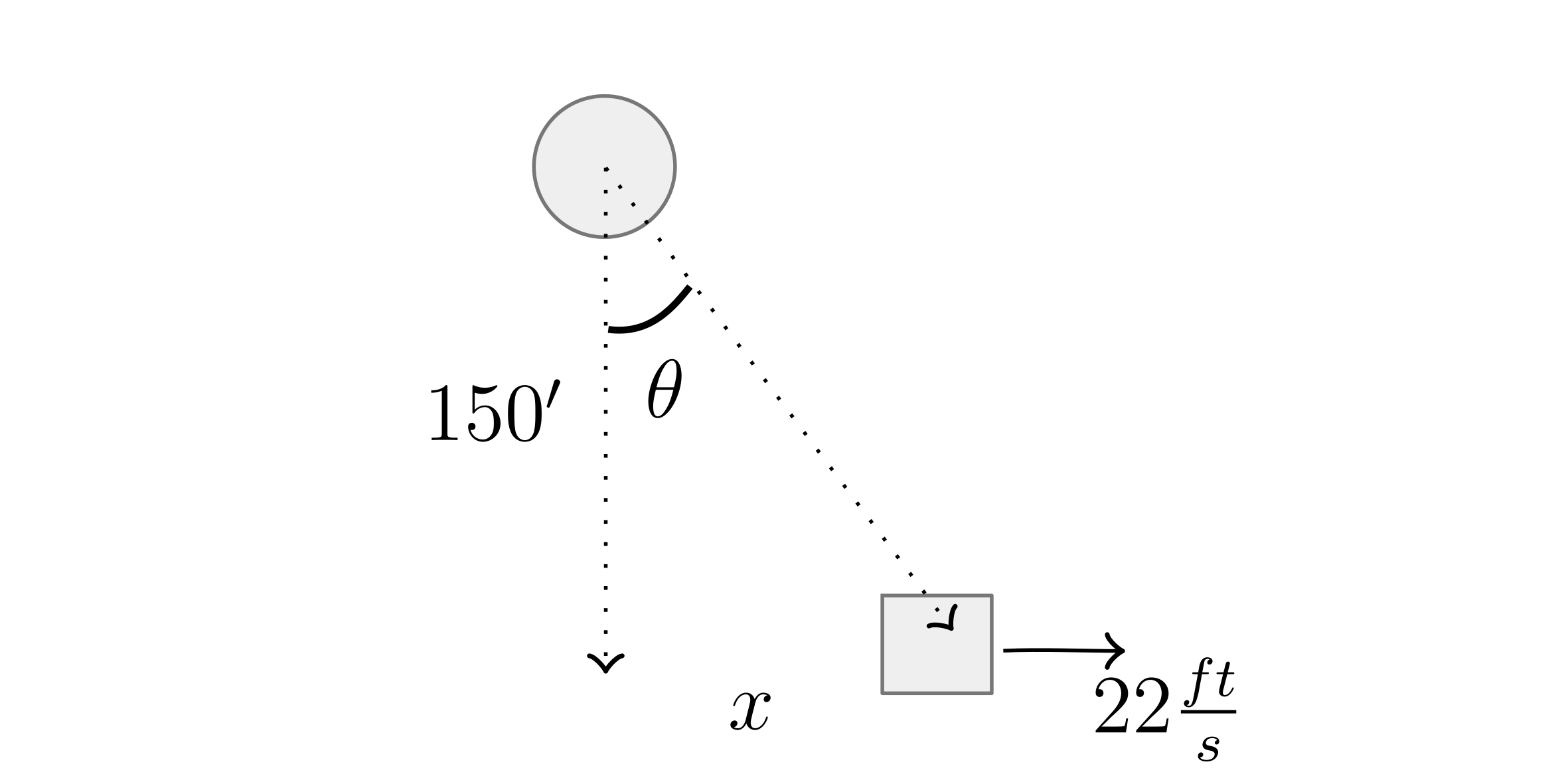
At what rate the spotlight turns when the person is at $x=50$ ft?

$\tan (\theta) = \frac{x}{150}$

$\theta = \tan ^{-1} (\frac{x}{150})$

$\frac{d \theta}{dt} = \frac{d}{dx} ( tan ^{-1} \frac{x}{150}) \frac{dx}{dt}$ (Chain rule)

Recall that $(\tan ^{-1})’ = \frac{1}{1+x^2}$

$\frac{d \theta}{dt} = \frac{1}{1+(\frac{x}{150})^2} \frac{1}{150} * 22$

$\frac{d \theta}{dt} \mid _{x=50} = \frac{22}{150} \frac{1}{1+ (\frac{50}{150})^2} = 0.132 \frac{rad}{seconds}$

Method 2:

$\tan (\theta) = \frac{x}{150}$

$\sec ^2 (\theta) * \frac{d \theta}{dt} = \frac{1}{150} \frac{dx}{dt}$

$\frac{d \theta}{dt} = \frac{1}{150} \frac{dx}{dt} cos^2 (\theta)$

$\frac{d \theta}{dt} = \frac{1}{150} 22 \frac{150^2}{(x^2 + 150^2)}$

Inverse Trig Identities

$\sin ^{-1} x + \cos^{-1} x = \frac{\pi}{2}$

$\tan^{-1} x + \cot^{-1} x = \frac{\pi}{2}$

$\sec^{-1} x + \csc^{-1} x = \frac{\pi}{2}$

Use $\sin (\frac{\pi}{2} - x) = \cos (x)$

Example (#2):

$p(z) = 17 \csc^{-1} \frac{z}{2}$ find $p’(z)$

Recall that $\csc^{-1} (x)’ = \frac{-1}{\mid x\mid \sqrt{x^2-1} }$

$p’(x) = \frac{17}{2} \frac{-1}{\mid \frac{z}{2}\mid \sqrt{(\frac{z}{2})^2 -1} }$

Example (#7):

$r(t) = \tan ^{-1} \sqrt{t}$ find $r’(t)$

$r’(t) = \frac{1}{1 + \sqrt{t}^2} \frac{1}{2} t^{\frac{1}{2}}$

3.3 Optimization

Case 1: Closed interval

Case 1: A closed, bounded interval [a, b]

Find critical points ($f’(x) = 0$) and evaluate $f$ here and at end points.

Example:

Find extrema $f(x) = 2x^3 - 3x^2 - 12x$ on [0, 3]

$f’(x) = 6x^2 - 6x - 12$ $f’(x) = 6(x^2 - x - 2)$ $f’(x) = 6(x^2 - x - 2) = 0$

Critical points: $x=2, -1$ but -1 is outside of our interval so we don’t worry about it.

$f(0) = 0$ $f(2) = -20$ $f(3) = -9$

Case 2: An open interval

Case 2: An open interval -> apply first or 2nd derivative test.

First derivative:

if $f’$ changes from positive to negative at $x=c$ then $f$ attains a max at $c$
if $f’$ changes from negative to positive at $x=c$ then $f$ attains a min at $c$

Second derivative:

if $f’’$ at $x=c$ is less than 0, $f$ has a max at $c$
if $f’’$ at $x=c$ is greater than 0, $f$ has a min at $c$

Example:

Find the extreme values of $y=f(x)=xe^{-x}$ on $(-\infty, \infty)$.

$f’(x) = xe^{-x}(-1) + e^{-x}(1)$

$f’(x) = e^{-x} (1-x)$

Critical points at $x=1$

First derivative test:

Intervals:

$(-\infty, 1),\ f’ > 0$ function is increasing
$(1, \infty),\ f’ < 0$ function is decreasing

Therefore we have a local and global max at $x=1$.

Second derivative test:

$f’‘(x) = (e^{-x} - xe^{-x})’ = e^{-x} (-1) - (xe^{-x}(-1) + e^{-x}(1))$

$f’‘(x) = e^{-x}(x-2)$

$f’‘(1) = e^{-1} (1-2) < 0$ so $x=1$ is a local and global max

Case 3: One critical point

Case 3: We are told, or physical reasons imply, that the extreme value is attained and there is one critical point.

Extreme value occurs at critical point

Example:

The function $f(x) = e^{-x} \sec(x)$ has a max on $(\frac{\pi}{2}, \frac{3\pi}{2})$, find it.

$f’(x) = e^{-x} \sec(x) \tan (x) + sec(x) e^{-x} (-1)$

$f’(x) = e^{-x} \sec(x) (\tan (x) - 1)$

This is when $\sin (x) = \cos (x)$ on the interval. So it occurs at $x=\frac{5\pi}{4}$.

What is the value? $e^{-\frac{5\pi}{4}} \sec(\frac{5\pi}{4}) = \frac{e^{\frac{-5\pi}{4}}}{\frac{-1}{\sqrt{2} }}$

Example:

A farmer has 2,400 ft of fence and wants the largest rectangular area he can make (along a river where we don’t need fence).

What are the dimensions?

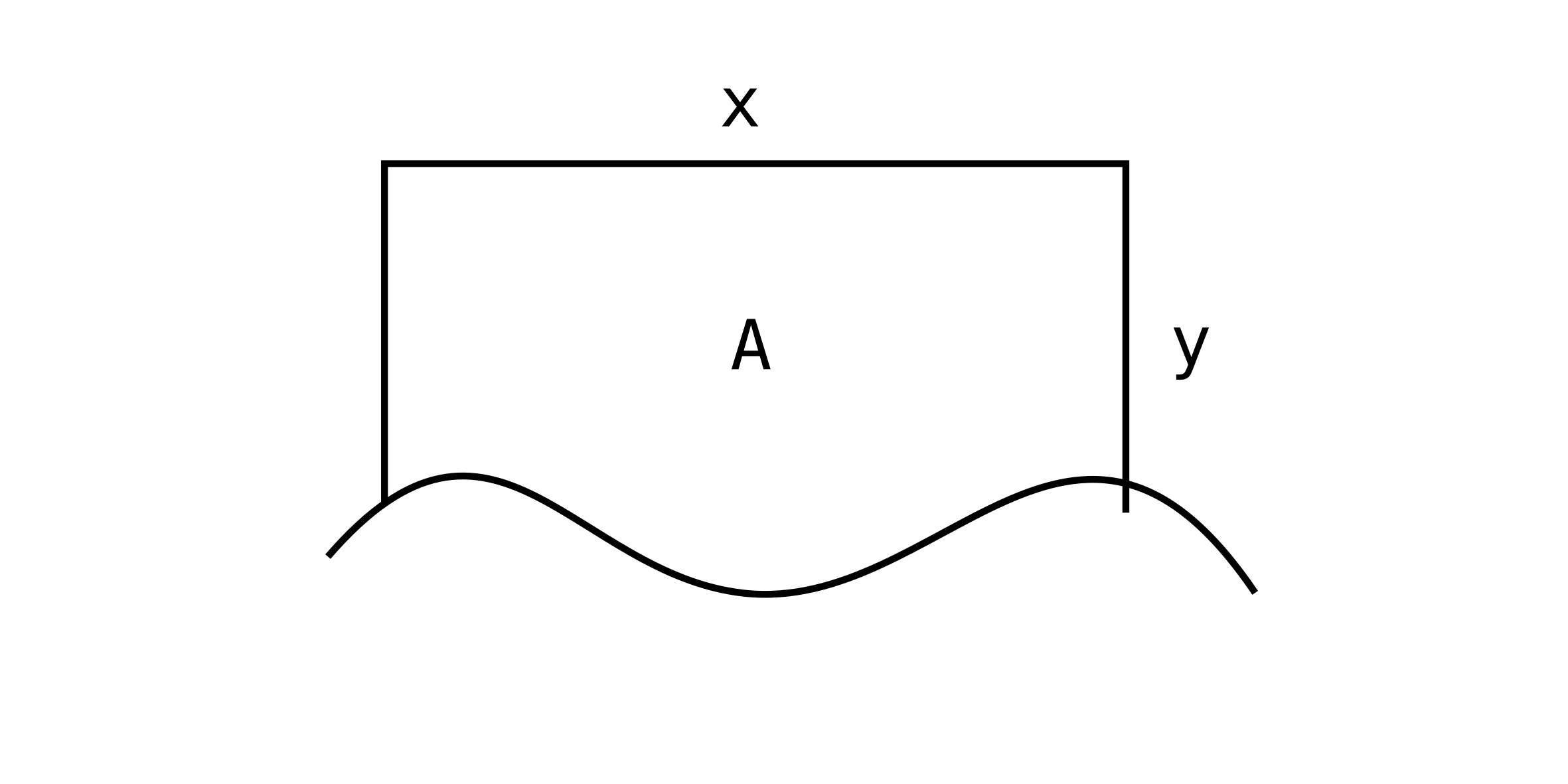
Optimize (maximize): $A = xy$

Given constraint: $2y + x = 2400$

$x = 2400 - 2y$

$\therefore A(y) = (2400 - 2y)y$

$\frac{dA}{dy} = 2400 - 4y$

Critical points: $y = 600$

So $x = 2400 - 2(600) = 1200$

Dimensions:

$x=1200,\ y=600$

Check that this is a max:

For $y < 600$, $A’(y) > 0$ For $y > 600$, $A’(y) < 0$

Yes, this is a maximum.

Example:

We want to construct a box with a square base and we have a total of $10m^2$ of material. What is the max volume and dimensions?

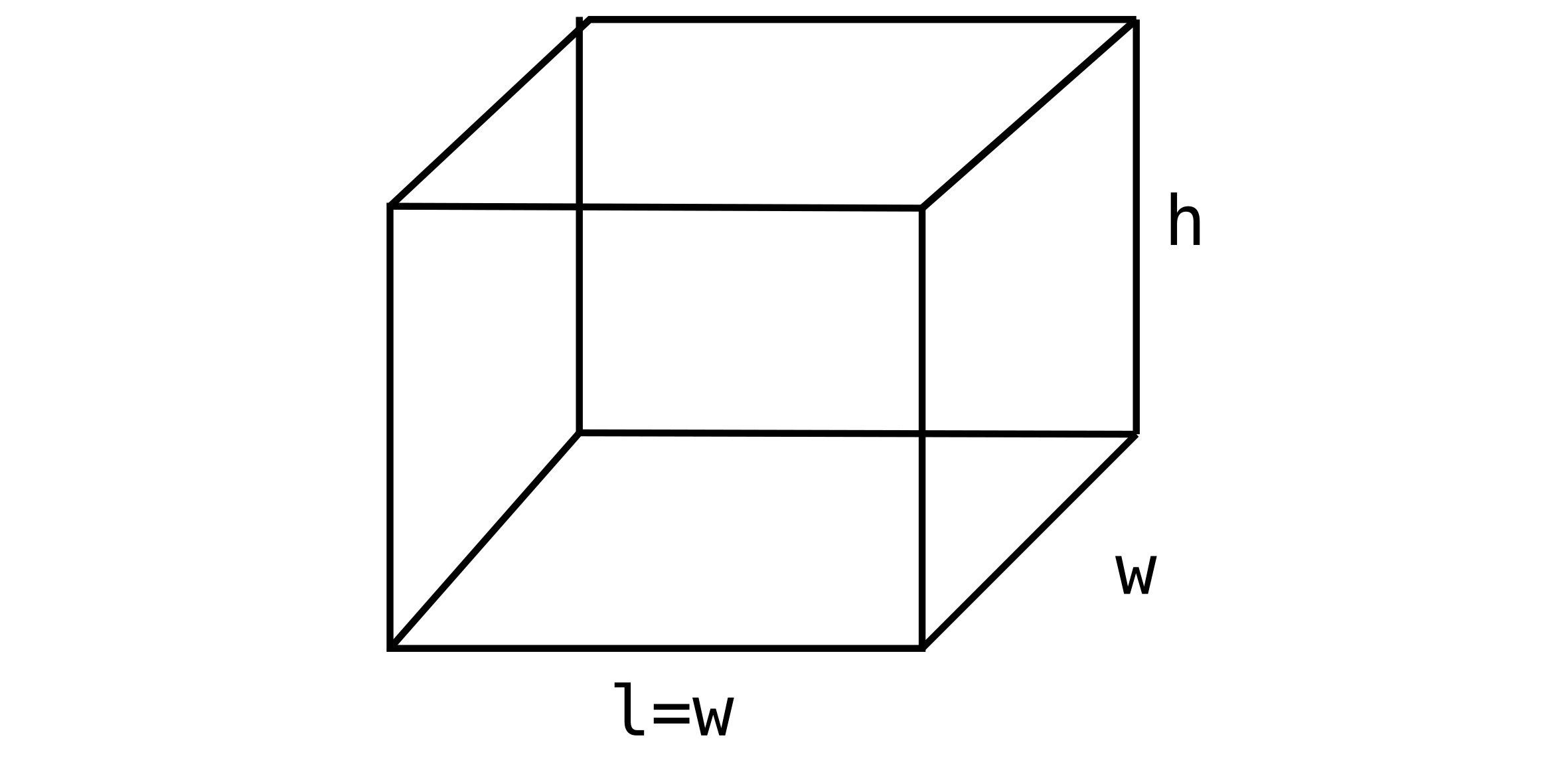
Optimize (maximize): $V = w^2 h$

Given constraints: surface area = $10m^2$

Surface area = front + back + 2 sides + top + bottom

Surface area = $2wh+2wh + 2w^2$

Surface area = $4wh + 2w^2 = 10$

$4wh = 10 - 2w^2$

$h = \frac{10-2w^2}{4w}$

$\therefore V = w^2h = w^2 \left( \frac{10 - 2w^2}{4w} \right)$

$V(w) = \frac{1}{2} \left( 5w - w^3 \right)$

$V’(w) = \frac{1}{2} \left( 5 - 3w^2 \right)$

Critical points: $w = \sqrt{\frac{5}{3}}$

$w < \sqrt{\frac{5}{3}} $, $V’(w) > 0$ $w > \sqrt{\frac{5}{3}} $, $V’(w) < 0$

Therefore $w = \sqrt{\frac{5}{3}}$ is a max.

Solving for $h$, we get $h = \sqrt{\frac{5}{3}}$

Example:

Aluminium can that holds $500cm^3$

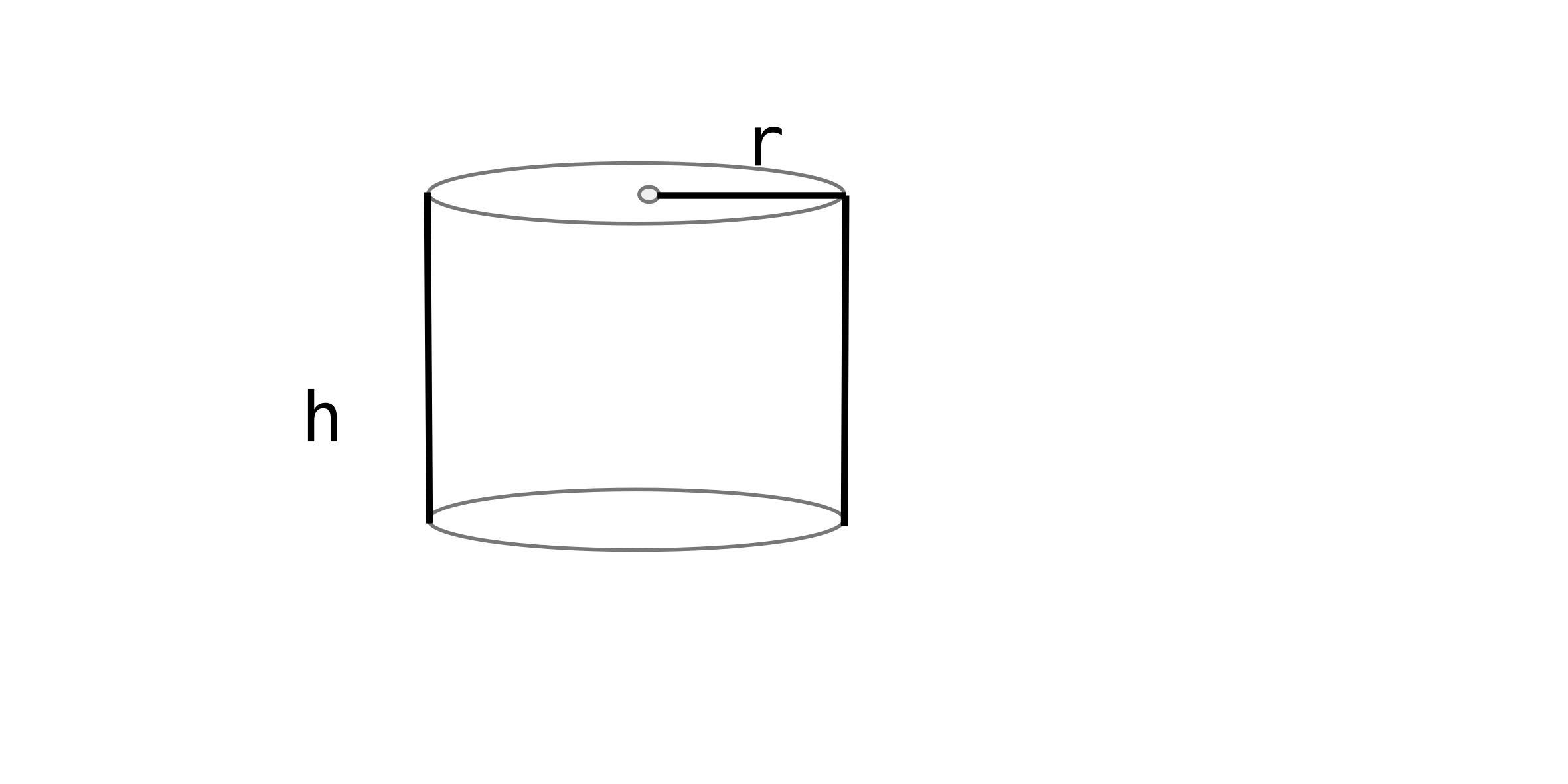
Assume the aluminum is thin

For sides, cost is $c$ dollars/$cm^2$

For top and bottom, cost is $2c$ dollars/$cm^2$

Find the dimensions $(r, h)$ that minimizes cost.

Optimize (minimize): Total cost $T$ = sides + top + bottom

$T = 2 \pi r h c + Tc 2 \pi r^2$

$T(r, h) = 2\pi r h c + 4\pi r^2 c$

Constraint: $V = \pi r^2 h = 500$

Solve for $h$:

$h = \frac{500}{\pi r^2}$

$T(r) = 2\pi rc \left( \frac{500}{\pi r^2} \right) + 4 \pi r^2 c$

$T(r) = 4c \left( \frac{250}{r} + \pi r^2 \right)$

$\frac{dT}{dr} = 4c \left( \frac{-250}{r^2} + 2\pi r \right) = 0$

$\frac{250}{r^2} = 2\pi r$

$r = \frac{5}{\pi ^{\frac{1}{3}}}$

$h = \frac{500}{\pi r^2}$

$\therefore h = 4r$

$\frac{d^2 T}{dr^2} = 4c(-250 (-2 r^{-3} + 2\pi)) $

$\frac{d^2 T}{dr^2} = 4c (\frac{500}{r^3} + 2\pi ) > 0$ for $r>0$ so $r$ is a minimum.

Example:

A piece of cardboard is 14 in by 10 in and we will fold the corners to make a box (with no top). What height will give the max volume?

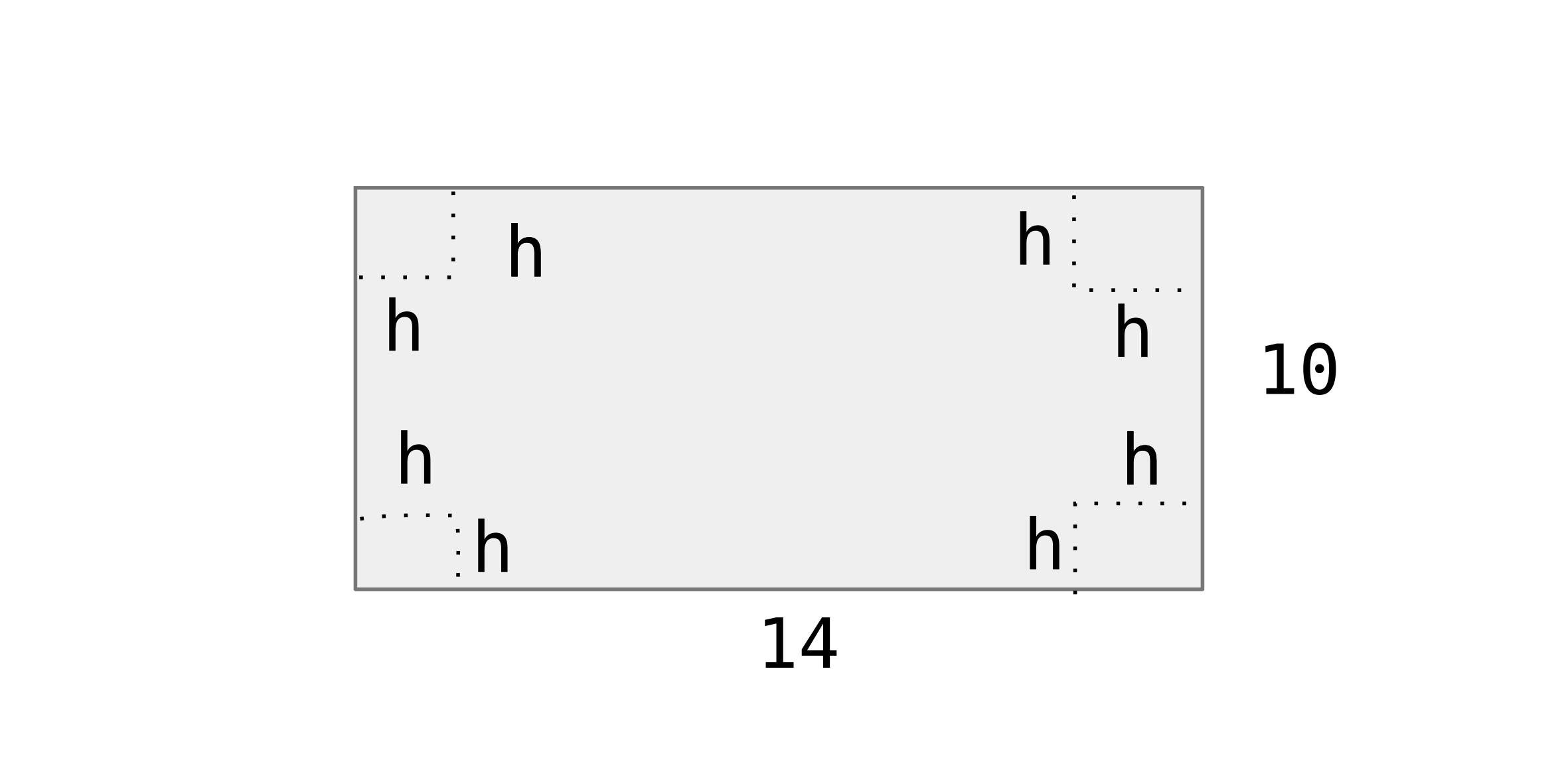
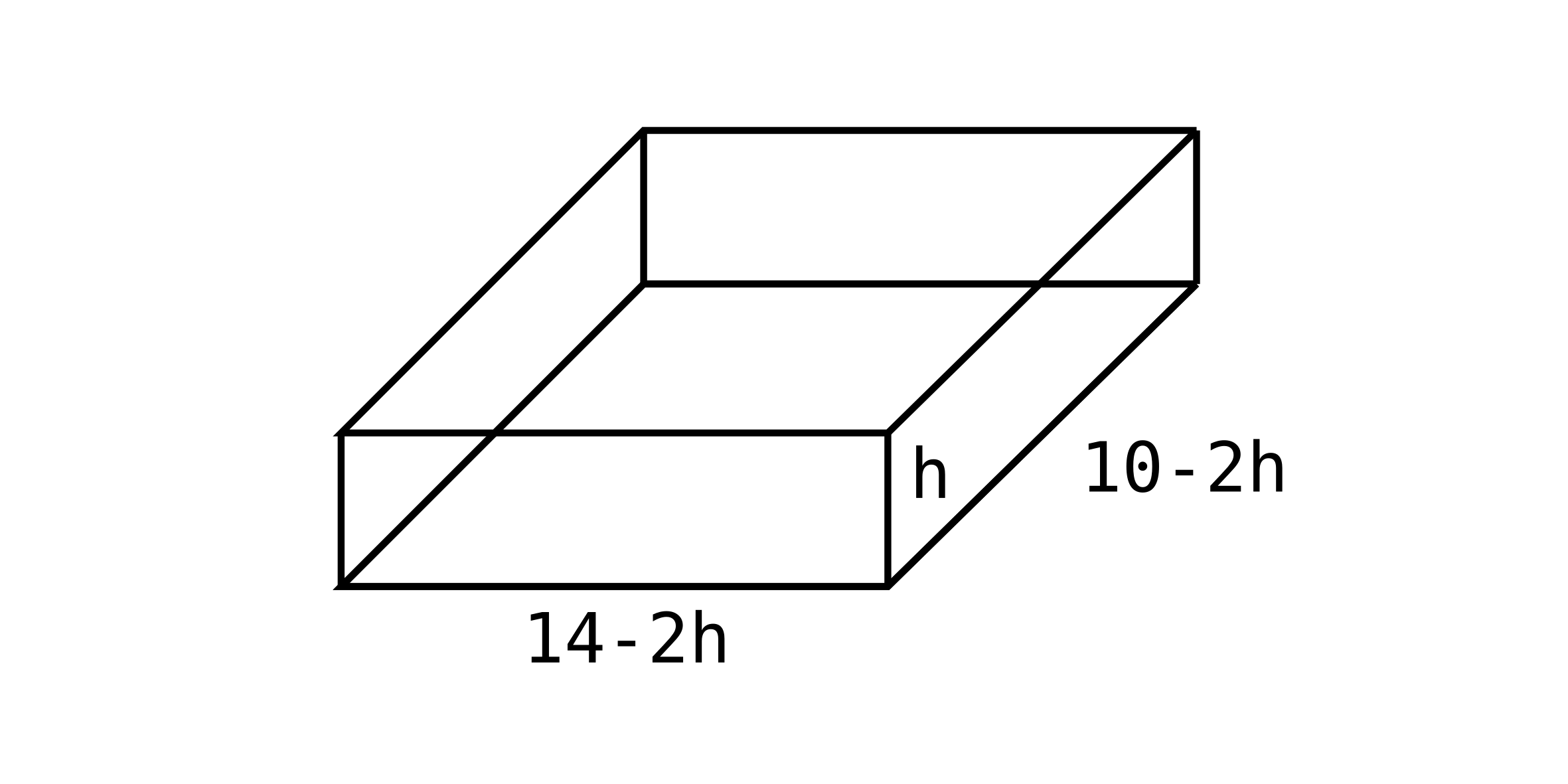
Optimize V (maximize): $V = lwh = (10-2h)(14-2h)h$ when $0 < h < 5$

$V = (14h-2h^2) (10-2h) = 140h - 28h^2 - 20h^2 + 4h^3 = 140h - 48h^2 + 4h$

$V’(h) = 140 - 96h + 12h^2$

$h = \frac{(-96) \pm \sqrt{(-96)^2 - 4(12)(140)} }{2(12)}$

$h \approx 1.92$ or $\approx 6.08$ (and 6.08 is too large)

$V’‘(h) = -96 + 24h$

$V’‘(1.92) \approx -96 + 24(1.92) < 0$ so the max volume is when $h \approx 1.92$ with a volume of $\approx 120.1 in^3$.

Example

What is the least amount that we can pay to have a pipe between the water main and the hydrant.

$40 / foot under the street

$20 / foot under ground

Cost = portion under street + portion under ground

$C = \sqrt{(40-x)^2 + 30^2}40 + 20x $

$\frac{dC}{dx} = 0 = 40 * \frac{1}{2} ((40-x)^2 + 30^2)^{\frac{-1}{2}} * 2 (40-x)(-1) + 20$

$20 = \frac{40 (40-x)}{((40-x)^2 + 30^2)^{\frac{1}{2}}}$

$((40-x)^2 + 30^2)^{\frac{1}{2}} = 2 (40-x)$

$(40-x)^2 + 30^2 = 4(40-x)$

$30^2 = 3(40-x)^2$

$300 = (40-x)^2$

$c\approx 22.68$

$C(22.68) = 40 * \sqrt{(40-22.68)^2 + 30^2} + 20(22.68) $

3.5 L’Hopital’s Rule

Recall $f’(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h}$

For h->0 we get $\frac{0}{0} = f’(x)$ which is an indeterminate form. imx→cf(x)g(x)=f′(x)g′(x)

(Note: we keep applying this rule until we get to a determinate form)

Example:

limt→∞tet Form: ∞∞

=limt→∞1et Form: 1∞ (no longer indeterminate) Other indeterminate forms:

$\lim_{x \to 0} \frac{x}{e^x}$ Form: $\frac{\infty}{\infty}$
$\lim_{x \to 0^+} x \ln (x)$ Form: $0 *(-\infty)$ (We have to apply this to a quotient before applying L’Hopital’s rule)

L’Hoptial’s Rule

For $f$ and $g$ differentiable on $(a, b)$, suppose $\lim_{x \to c} f(x) = \pm \infty$ or $f(x) = 0$ and $\lim_{x \to c} g(x) = \pm \infty$ or $g(c) = 0$

Suppose $\lim_{x \to c} \frac{f’(x)}{g’(x)}$ exists

Then $\lim_{x \to c} \frac{f(x)}{g(x)} = \frac{f’(x)}{g’(x)}$ (Note: we keep applying this rule until we get to a determinate form)

Example:

$\lim_{t \to \infty} \frac{t}{e^t}$ Form: $\frac{\infty}{\infty}$

$= \lim_{t \to \infty} \frac{1}{e^t}$ Form: $\frac{1}{\infty}$ (no longer indeterminate)

$= 0$

Example:

$\lim_{t \to \infty} \frac{t^3}{e^t} = \lim_{t \to \infty} \frac{3t^2}{e^t} = \lim_{t \to \infty} \frac{6t}{e^t}$

$= \lim_{t \to \infty} \frac{6}{e^t} = 0$

Example:

Calculate $\lim_{x \to 0} \frac{x-\sin (x)}{x^3}$ Form: $\frac{0}{0}$

$\lim_{x \to 0} \frac{1-\cos(x)}{3x^2} = \lim_{x \to 0} \frac{\sin(x)}{6x} = \lim_{x \to 0} \frac{\cos(x)}{6} = \frac{1}{6}$

Example:

A particle is moving on x-axis and its position is $x=(1-t) \ln (1-t)$ for $0\le t\le 1$ as $t$ goes to 1, what happens to the position?

$\lim_{t \to 1} (1-t) \ln (1-t)$ Form: $0 \infty$

Rewrite as quotient:

$\lim_{t \to 1^-} \frac{\ln (1-t)}{\frac{1}{1-t}}$ Form: $\frac{\infty}{\infty}$

$\lim_{t \to 1^-} \frac{\frac{1}{1-t}(-1)}{\frac{1}{(1-t)^2}} = \lim_{t \to 1^-} (1-t)(-1) = 0$

4.1 What is a Differential Equation?

It’s just an equation with a derivative in it.

Consider free fall.

$v = \frac{dy}{dt} = -a t$

$y = -a \frac{1}{2} t^2 + C$

Because velocity is the derivative of the position, we can call the position the anti-derivative of the velocity.

Suppose we have some initial value at the beginning $y(0) = 25m$.

$25m = \frac{-1}{2} a(0) ^2 + C $

$\therefore C = 25$

$y(t) = \frac{-1}{2} at^2 + 25$

First Order Differential Equations: $\frac{dy}{dx} = f(x)$ (Characteristic Differentiation)

We want to find $y = F(x)$ such that $F’(x) = f(x)$

Some Differential Equations

Hooke’s Law

$mx’’ = -kx$

$\therefore x’’ = -\frac{k}{m}x = -\Omega ^2 x$

Solutions $x = c_1 \cos (\omega t) + c_2 \sin (\omega t)$

Radioactive Decay

$\frac{dA}{dt} = -kA$

Solution $A(t) = A_o e^{-kt} = A_o (\frac{1}{2}) \frac{t}{t_{0.5}}$

See text for mixing problem

$\frac{dP}{dt} = 2 - \frac{P}{25}$ (2 and $\frac{P}{25}$ come from initial conditions)

$P = 50-40 e^{\frac{-t}{25}}$

Population growth

$\frac{dN}{dt} = rN$ (where r is the growth rate)

$N(t) = Ce^{rt}$

Consider $\left( \frac{dy}{dx} \right) ^2 = 1-y^2$

Possible solutions

$y_1 = \sin ^2 (x)$

$y_2 = \sin (x)$

Only $y_2$:

$\frac{dy_2}{dx} = \cos (x)$

$(\cos x)^2 = 1 - \sin ^2 (x)$

Example (#44):

A spherical chunk of ice melts so that its rate of volume decrease is proportional to the exposed surface area.

a. Write out the differential equation in terms of V and surface area

b. Use equations for V and surface area to find the equations in terms of radius

c. Find the volume of the chunk if r(0) = 0.25m

$\frac{dV}{dt} \propto -S$

$\frac{dV}{dt} = - kS$

$\frac{d}{dt} \left( \frac{4}{3} \pi R^2 \right) = -k (4\pi R^2)$

$\frac{dR}{dt} = -k$

$\int dR = - \int k dt$

$R = -kt + C$

Initial value $R(0) = 0.25m$

$R(0) = -k(0) + C$

$R(t) = -kt + 0.25$

$V = \frac{4}{3}\pi (-kt + 0.25)^3$

4.2 (or 1.2 in the new book) Anti-Derivatives

Given $\frac{dy}{dx} = f(x)$

We want $y = F(x)$ such that $F’(x) = f(x)$

$\int (f(x)) dx$ = indefinite integral of $f(x)$

($f(x)$ is the integrand)

$\int (\ ) dx$ is the inverse of $\frac{d}{dx}(\ )$

Example:

$\frac{dy}{dx} = x^2 - 2$

$y = F(x) = \frac{1}{3}x^3 - 2x$ is one solution

$y = \frac{1}{3}x^3 - 2x + C$ is the general solution

Power Rule for Integration

$\int 0 dx = C$
$\int 1 dx = x + C$
if $p \neq -1$ $\int x^p dx = \frac{1}{p+1} x^{p+1} + C$
$\int x^{-1} dx = \int \frac{1}{x} dx = \log \mid x \mid + C$

Example

Solve the initial value problem

$\frac{dP}{dr} = \sqrt{r} $

$P(9) = 7$

$P(x) = \frac{2 x^{\frac{3}{2}}}{3} + C$

$P(9) = 7 = \frac{2 x^{\frac{3}{2}}}{3} + C$

$\therefore C = -11$

$P(r) = \frac{2}{3}r^{\frac{3}{2}} - 11$

Linearity of Derivatives (and anti-derivatives)

If a and b are constants then $\int (a f(x) + b g(x)) dx = a \int f(x) dx + b \int g(x) dx$.

Example:

$\int (x + x^2) dx = \int x dx + \int x^2 dx = \frac{1}{2}x^2 + \frac{1}{3}x^3 + C$

Other Integration Formula:

$\int \cos (x) dx = \sin(x) + C$

$\int \sin (x) dx = -cos (x) + C$

$\int e^x dx = e^x + C$

On open $I = (-1, 1)$: $\int \frac{1}{\sqrt{1-x^2} } dx = sin ^{-1} (x) + C$

On open $I = (-\infty, \infty)$: $\int \frac{1}{1+x^2} = \tan ^-1 (x) + C$

Example:

Suppose the acceleration of an object moving in a straight line is $a=\sin(t)$. Find the velocity and the position in terms of their initial values $v_o$ and $p_o$.

$v = \int a dt$

$v = -\cos(t) + C$

$v_o = -\cos(0) + C$

$\therefore C = v_o + 1$

$\fbox{$v = -\cos(t) + v_o + 1$}$

$p = \int v dt$

$p = -\sin (t) + \int v_o dt + \int 1 dt$

$p = -\sin (t) + v_o t + t + C$

$p_o = -\sin (0) + 0 + 0 + C$

$\therefore C = p_o$

$\fbox{$p = -\sin (t) + v_o t + t + p_o$}$

The Chain Rule in Anti-Derivative Form (Integration by Substitution)

If f' and g' are differentiable, then $\int (f’(g(x)) * g’(x)) dx= f(g(x)) + C$.

Or let $u=g(x)$

$\int f’(u) \frac{du}{dx} dx = \int f’(u) du = f(u) + C$

Example:

Calculate the integrals of:

*. $\int \cos (e^x + 7) * e^x dx$

$u = e^x + 7$

$\frac{du}{dx} = e^x$ $du = e^x dx$

$\int \cos (u) du = \fbox{$\sin (u) + C + \sin (e^x + 7) + C$}$

Check:

$(\sin (e^x + 7) + C)’ = \cos(e^x + 7) e^x$

*. $\int \frac{t}{1+t^2} dt$

$u = 1+t^2$

$du = 2t dt$

$\int \frac{t}{u} \frac{du}{2t} = \frac{1}{2} \int \frac{1}{u} du$

$= \frac{1}{2} \ln \mid 1+t^2 \mid + C$

Note that $1+t^2 > 0 \forall t$

$= \fbox{$\frac{1}{2} \ln (1+t^2) + C$}$

Examples:

$\int (1- \frac{1}{w}) \cos (w - \ln (w)) dw$

$u=w - \ln w$ $du = 1 - \frac{1}{w} dw$

$\int \cos (u) du = \fbox{$\sin (w- \ln w) + C $}$

$\int \frac{x}{\sqrt{1-4x^2}} dx$

$u = 1-4x^2$ $du = -8 x dx$

$\frac{1}{-8} \int \frac{1}{\sqrt{u} } du$

$\fbox{$= \frac{-\sqrt{1-4x^2}}{4} + C$}$

$\int (\frac{5}{w} - 7e^w + 6w^{\frac{1}{3}}) dw$

$\int \frac{5}{w} dw - 7 \int e^w dw + 6 \int w^{\frac{1}{3}} dw$

$\fbox{$= 5\ln \mid w \mid - 7 e^{w} + \frac{9}{2} w^{\frac{4}{3}}$}$

$\int \sin (1-x) (2 - \cos (1-x))^4 dx$

$u = 2-cos(1-x)$

$du = \sin(1-x)(-1) dx$

$=-1\int u^4 du$

$\fbox{$= \frac{-1}{5}(2- \cos(1-x))^5 + C$}$

Example:

Which ones of the examples below are probably logs, powers, or inverse trig?

1: $\int \frac{3}{5y + 4} dy$

$u = 5y + 4$

$du = 5 dy$

$\therefore dy = du \frac{1}{5}$

$3 \int \frac{1}{u} du \frac{1}{5}$

$\frac{3}{5} \ln (u) + C$

$\fbox{$\frac{3 \ln (5y + 4)}{5} + C$}$

2: $\int \frac{3y}{5y^2 + 4} dy$

$u = 5y^2 + 4$

$du = 10y dy$

$\therefore dy = \frac{1}{10y} du$

$\int \frac{3y}{u} \frac{1}{10y} du$

$\frac{3}{10} \int \frac{1}{u} du$

$\frac{3}{10} \ln (u) + C$

$\fbox{$\frac{3 \ln (5y^2 + 4)}{10} + C$}$

3: $\int \frac{3y}{(5y^2 + 4)^2} dy$

Power

$u = 5y^2 + 4$

$du = 10y dy$

$\therefore dy = \frac{1}{10y} du$

$\int \frac{3y}{u^2} \frac{1}{10y} du$

$\frac{3}{10} \int \frac{1}{u^2} du$

$\frac{-3}{u} + C$

$\fbox{$\frac{-3}{5y^2 + 4} + C$}$

4: $\int \frac{3}{5y^2 + 4}$

Inverse trig

$3 \int \frac{1}{4 \left( \frac{5y^2}{4} + 1 \right)}$

$u = \frac{\sqrt{5}y}{2} dy$

$du = \frac{\sqrt{5}}{2} dy$

$\frac{3}{4} \int \frac{1}{u^2 + 1} du \frac{2}{\sqrt{5} }$

$\frac{6}{4 \sqrt{5} } \int \frac{1}{u^2 + 1} du$

$\frac{3}{2 \sqrt{5} } \tan ^{-1} (u) + C$

$\fbox{$\frac{3}{2 \sqrt{5}} \tan ^{-1} \left( \frac{\sqrt{5} y}{2} \right) + C$}$

2.1 Sums and Differences

Sums

Sigma notation

$\sum_{k=m}^{n} f(k) = f(m) + f(m+1) + … + f(n - 1) + f(n)$

$f(k) = f_k$

$\sum_{k=-1}^{3} k^2 = (-1)^2 + (0) ^ 2 + 1^2 + 2^2 + 3^2 = 15$

We can split this up into $\sum_{j=-1}^{0} j^2 + \sum_{j=1}^{3} j^2$

$\sum_{j=-1}^{3} j^2 = \sum_{j=1}^{0} j^2 + \sum_{j=1}^{3} j^2$

Splitting Sums

$\sum_{k=m}^{p} f_k = \frac{k=m}{n} f_k + \sum_{k=n+1}^{p} f_k$

Shifting

$\sum_{j=-1}^{3} j^2$

Suppose we want this sum to start at 1

Let $k = j+2$. Therefore $j = k-2$

$= \sum_{k=1}^{5} (k-2)^2 = (1-2)^2 + (2-2)^2 + (3-2)^2 + (4-2)^2 + (5-2)^2$

$= (-1)^2 + 0^2 + 1^2 + 2^2 + 3^2$

Consider another example:

$\sum_{l=3}^{7} l^2 = \sum_{l=1}^{5} (l+2)^2$

Proposition:

$\sum_{k=m}^{n} f_k = \sum_{k=m+p}^{n+p} f_{k-p}$

Linearity:

$\sum_{k=7}^{9} 1.7k^2 - \sqrt{3} \sin (k)$

$= 1.7(7^2) - \sqrt{3} \sin(7) + 1.7 (8)^2 - \sqrt{3} \sin(8) +$

$ 1.7 (9)^2 - \sqrt{3} \sin (9)$

We can take out the constant:

$= 1.7 \sum_{k=7}^{9} k^2 - \sqrt{3} \sum_{k=7}^{9} \sin (k)$

Generally:

$\sum_{k=m}^{n} (af_k + bg_k) = a \sum_{k=m}^{n} f_k + b \sum_{k=m}^{n} g_k$

Now use these methods to combine these sums.

$2 \sum_{k=3}^{50} k(k-1) - \sum_{k=1}^{50} (k+1)(k+2)$

Method 1: Break off the first 2 terms of the second sum and combine

$2 \sum_{k=3}^{50} k(k-1) - ( \sum_{k=3}^{50} (k+1)(k+2) + \sum_{k=1}^{2} (k+1)(k+2))$

$-18 + \sum_{k=3}^{50} 2k^2 - 2k - (k^2 + 3k + 2)$

$-18 + \sum_{k=3}^{50} (k^2 - 5k - 2)$

Method 2: Shift sum of right and split off top 2 terms

$\sum_{k=3}^{50} 2 k (k-1) - \sum_{k=3}^{52} (k-2 + 1)(k-2+2)$

$\sum_{k=3}^{50} 2k(k-1) - \sum_{k=3}^{50} k(k-1) + 51(51-1) + (52)(52-1)$

$-50(51) - (51)(52) + \sum_{k=3}^{50} k(k-1)$

Differences

Finite Difference Function: $\Delta f$

$\Delta f(k) = k(k) - f(k-1)$

Example

$\Delta k^2 = k^2 - (k-1)^2$

$= k^2 - (k^2 - 2k + 1)$

$= 2k-1$

So if $f(k) = k^2$, then $\Delta f(k) = 2k-1$

Linearity (of Differences):

$\Delta (a f(k) + b g(k)) = a \Delta f(k) + b \Delta g(k)$

Telescoping Sums:

$\sum_{k=m+1}^{n} \Delta f(k) = f(n) - f(m)$

Example: let m=1, n=4

$\sum_{k=1+1}^{4} \Delta k^2 = (2^2 - 1^2) + (3^2 - 2^2) + (4^2 - 3^2) + (5^2 - 4^2) = 5^2 - 1^2$

For b constant

$\Delta k = 1 = (k) - (k-1)$
$\Delta k^2 = 2k-1$
$\Delta k^3 = 3k^2 - 3k + 1$
$\Delta b^{k+1} = b^k (b-1)$

Consider $\Delta k^2 = 2k - \Delta k$

$k = \frac{1}{2} \Delta (k^2 + k)$

$k = \frac{\Delta (k(k+1))}{2}$

Finite Difference Formulae

$k = \Delta \frac{k(k+1)}{2}$
$k^2 = \Delta \left( \frac{k(k+1)(2k+1)}{6}\right)$
$b^k = \Delta \frac{b^{k+1}}{b-1}$

If we sum over both sides, if $n \ge 1$, the following are true:

$\sum_{k=1}^{n} k = \frac{n(n+1)}{2}$

$\sum_{k=1}^{n} k^2 = \frac{n(n+1)(2n+1)}{6}$

If $n\ge 0$ and $b \neq 1$, $\sum_{k=0}^{n} b^k = \frac{b^{n+1}}{b-1}$

Example:

Simplify $-18 + \sum_{k=3}^{50} (k^2 - 5k - 2)$

$-18 + \sum_{k=1}^{48} ((k+2)^2 - 5(k+2) - 2)$

$-18 + \sum_{k=1}^{48} (k^2 + 4k + 4 - 5k+10 - 2)$

$-18 + \sum_{k=1}^{48} (k^2 - k - 8)$

$-18 + \sum_{k=1}^{48} k^2 - \sum_{k=1}^{48} k - \sum_{k=1}^{48} 8)$

$-18 + \frac{48 (48+1)(2 * 48 + 1)}{2} + \frac{48 * 49}{2} - 48 * 8$

Simplify $-(50)(51) - (51)(52) + \sum_{k=1}^{48} (k+2)(k+2-1)$

$-(50)(51) - (51)(52) + \sum_{k=1}^{48} k^2 + 3k + 2$

$-(50)(51) - (51)(52) + \sum_{k=1}^{48} k^2 + 3 \sum_{k=1}^{48} k + 2 * 48$

$-(50)(51) - (51)(52) + \frac{48(49)((2)(48) + 1)}{6} + \frac{3 (48)(49)}{2} + 2(48)$

Simplify $\sum_{k=3}^{50} 2k (k-1) - (\sum_{k=1}^{48} k^2 + 3k + 2 + \sum_{k=49}^{50} (k^2 + 3k + 2))$

$\frac{48 (49)(2(48) + 1)}{6} + 3 \frac{48(49)}{2} + 2 (49) - 5202$

All three of these are what we got previously (and therefore should all result in the same number).

Example:

$\sum_{k=3}^{7} (3k + 2)$

$\sum_{k=1}^{5} 3 (k+2) + 2$

$\sum_{k=1}^{5} (3k + 8)$

$3 * \sum_{k=1}^{5} k + \sum_{k=1}^{5} 8$

$3 * \frac{5 * 6}{2 + 8*5}$

$= 85$

Example:

$\sum_{j=2}^{5} j^2 - j$

$\sum_{j=1}^{8} (j-3)^2 - (j-3)$

$\sum_{j=1}^{8} -6 j + 9 - j +3$

$\sum_{j=1}^{8} j^2 - 7j + 12$

$\sum_{j=1}^{8} j^2 - 7 \sum_{j=1}^{8} j + \sum_{j=1}^{8} 12$

$= \frac{8 * 9 (2 * 8 + 1)}{6} - 7 \frac{8 * 9}{2} + 8 * 12$

$=48$

2.3 Prelude to the Definite Integral. Riemann Sums

The limit of the Riemann Sums is the Definite Integral.

Consider a car driving. It has a certain position and velocity at a given time. You can take the derivative of position to get the velocity. Can we go back from velocity to position? Yes; with the anti-derivative.

$0 \le t_1 \le 0.3s\ v=30 \frac{m}{s}$

$0.3 < t_2 \le 0.8s\ v=20 \frac{m}{s}$

$0.8 < t_3 \le 1.2s\ v=10 \frac{m}{s}$

$1.2 < t_4 \le 2s\ v=-2 \frac{m}{s}$

We want to find the displacement between $t=0$ and $t=2.0$. This is $p(2) - p(0)$.

We can expand that to be $p(2) - p(1.2) + p(1.2) - p(0.8) + p(0.8) - p(0.3) + p(0.3) - p(0)$

$\frac{p(2) - p(1.2)}{2-1.2} \approx -2 \frac{m}{s}$ which is $\Delta p = v \Delta t$

Now we have to do this with all other intervals:

$\frac{p(1.2) - p(0.8)}{1.2 - 0.8} \approx 10 \frac{m}{s} \therefore \Delta p = 10(0.4)$

$\frac{p(0.8) - p(0.3)}{0.8 - 0.3} \approx 20 \frac{m}{s} \therefore \Delta p = 20(0.5)$

$\frac{p(0.3) - p(0)}{0.8 - 0} \approx 30 \frac{m}{s} \therefore \Delta p = 30(0.3)$

So therefore we can say that $p(2) - p(0) \approx -1.6 + 4.0 + 10 + 9 = 21.4 m$

We partitioned the time interval:

$P = { 0,0.3,0.8,1.2,2.0 }$

Largest sub interval is called the mesh: $\mid \mid P \mid \mid =0.8$

Example:

Let $P = { x_0, …, x_n }$ be a partition of $[a, b]$

Let $S = { s_1, …, s_n }$ be a set of sample points

Then the Riemann Sum, $R^{S}_P (f)$, of $f$ with respect to P and S is:

$\sum_{i=1}^{n} f (s_i) \Delta x_i = f(s_1)(x_1 - x_0) + f(s_2)(x_2 - x_1) + …$

$+ f(s_{n-1}) (x_{n-1} - x_{n-2}) + f(s_n) (x_n - x_{n-1})$

This is an estimate of the area under the function in that interval.

Example:

Consider a rod (shown above) of length 1 meter. The cross-sectional area is $0.01m^2$.

The density of the rod is $p(x) = (1+x) \frac{kg}{m^3}\ 0\le x\le 1$

We want the mass of the rod.

$M = p V$

Partition the interval into $[a,b]$ into 5 chunks (n).

$\Delta x = \frac{b-a}{n} = \frac{1-0}{5} =0.2 m$

So $P = { 0,0.2,0.4,0.6,0.8,1}$

$\mid \mid P \mid \mid = 0.2$

Volume $\approx \Delta x *$ cross sectional area (a) surrounding the point x.

Mass = $p(x) A \Delta x$

Our Riemann sum: $F_n$ * interval

$f(x) = p(x)A = 0.01 (1+x) \frac{kg}{m}$

For $0\le x \le 1$, $M(x)$ is mass between 0 and x so that if $0 \le a\le b\le 1$

$M(b) - M(a)$ is the mass between x=a and x=b.

$L = { 0, 0.2, 0.4, 0.6, 0.8 }$ (Note, we don’t need to write 1 because the last sampling will be 0.8 – we are sampling via the left for everything)

$[x_{i-1},\ x_i] (m)$

$f(s_i) \frac{kg}{m}$

$\Delta M (kg)$ this equals the approximate total.

For left-hand sample points:

[0,0.2], [0.2,0.4], [0.4, 0.6], [0.6, 0.8], [0.8, 1]

We sample with 0, 0.2, 0.4, 0.6, 0.8 respectively.

$f(s_i) = 0.01(1+s_i)$

$[x_{i-1}, x_i]$	[0,0.2]	[0.2,0.4]	[0.4,0.6]	[0.6,0.8]	[0.8,1]
$s_i$	0	0.2	0.4	0.6	0.8
$f(s_i)$	0.01(1)	(0.01)(1.2)	0.01(1.4)	0.01(1.6)	0.01(1.8)
$\Delta M (kg)$	0.01(1)(0.2)	(0.01)(1.2)(0.2)	0.01(1.4)(0.2)	0.01(1.6)(0.2)	0.01(1.8)(0.2)

Approx total

$M = R^{L}_{P} (f) \Delta x = 0.01(0.2)(1+1.2+1.4+1.6+1.8) = 0.014 kg$

Now, for right-hand sample points, use $R = { 0.2, 0.4, 0.6, 0.8, 1 }$ which would mean that your $s_i = 0.2, 0.4, 0.6, 0.8, 1$ for the intervals (respective).

$R^{R}_{P} (f) \Delta x = 0.01(0.2)(1.2 + 1.4 + 1.6 + 1.8 + 2) = 0.016 kg$

And for mid-point sample points, $C = { 0.1, 0.3, 0.5, 0.7, 0.9 }$. Plugging that into the Riemann Sum, we get $R^{C}_{P} (f) \Delta x = 0.01(0.2)(1.1 + 1.3 + 1.5 + 1.7 + 1.9) = 0.015 kg$

Now we want n subintervals, find $\Delta x_i = \frac{1-0}{n}= \frac{1}{n}$

$P_n = {0, \frac{1}{n}, \frac{2}{n}, \frac{3}{n}, …, \frac{n-1}{n}, 1}$

$L_n = {0, \frac{1}{n}, \frac{2}{n}, …, \frac{n-1}{n} }$

Note: $s_i = \frac{i-1}{n}$

Riemann Sum: $\sum_{i=1}^{n} f(s_i) \Delta x_i$

$\sum_{i=1}^{n} \left( \frac{i-1}{n} \right) \frac{1}{n} = \sum_{i=1}^{n} 0.01(1 + \frac{i-1}{n}) \frac{1}{n}$

$= \frac{0.01}{n}[ \sum_{i=1}^{n} 1 + \frac{1}{n}\sum_{i=1}^{n} i - \frac{1}{n} \sum_{i=1}^{n} 1]$

$= \frac{0.01}{n}[n + \frac{n+1}{2} - 1]$

$= \frac{0.01}{n}\left( \frac{3n-1}{n} \right)$

$\lim_{n \to \infty} \frac{0.01}{2}(3 - \frac{1}{n})$

$= 0.015 kg$

We want to now get the limit as the cross-sections become smaller with the right and center Riemann Sum.

Recall that our partition was $P(n) = { 0, \frac{1}{n}, \frac{2}{n}, …, \frac{n-1}{n}, 1 }$

Right sample set (excluding first point) $R_n = { \frac{1}{n}, \frac{2}{n}, …, \frac{n-1}{n}, 1 }$

$s_i = \frac{i}{n}$

So $R_{P}^{R} (f) = \sum_{i=1}^{n} f (\frac{i}{n}) \frac{1}{n} = \sum_{i=1}^{n} 0.01 (1 + \frac{i}{n}) \frac{1}{n}$

$= \frac{0.01}{n} [ \sum_{i=1}^{n} 1 + \frac{1}{n} \sum_{i=1}^{1} i ]$

$= \frac{0.01}{n} [ n+ \frac{1}{n} \frac{n(n+1)}{2} ]$

$= \frac{0.01}{n} [ \frac{2n + n + 1}{2n} ]$

$= \frac{3n + 1}{200n}$

$= \lim_{n \to \infty} \frac{3n + 1}{200n} = 0.01(\frac{3}{2}) = 0.015kg$

Now for the mid-point Riemann Sum.

$L_n = { 0, \frac{1}{n}, \frac{2}{n}, … \frac{n-1}{n} }$

$R_n = { \frac{1}{n}, \frac{2}{n}, …, 1 }$

Center is just the average of left and right.

$C_n = (0+\frac{1}{n}) \frac{1}{2}, (\frac{1}{n}+\frac{2}{n}) \frac{1}{2}, …, (\frac{n-1}{n} + 1) \frac{1}{2}$

$C_n = \frac{1}{2n}, \frac{3}{2n}, …, \frac{2n-1}{2n}$

$S_i = \frac{2i - 1}{2n}$

$R_{P}^{C} (f) = \sum_{i=1}^{n} 0.01 (1 + \frac{2i-1}{2n}) \frac{1}{n}$

$= \frac{0.01}{n} [ \sum_{i=1}^{n} 1 + \frac{1}{n} \sum_{i=1}^{n} i - \frac{1}{2n} \sum_{i=1}^{n} 1 ]$

$= \frac{0.01}{n} [n + \frac{1}{n} \frac{n(n+1)}{2} - \frac{1}{2} ]$

$= \frac{0.01}{n} [ \frac{2n}{2} + \frac{n+1-1}{2} ]$

$= \frac{0.01 (3)}{2} = 0.015 kg$

Example:

Consider the graph $y= f(x) = 0.01 (1+x)$

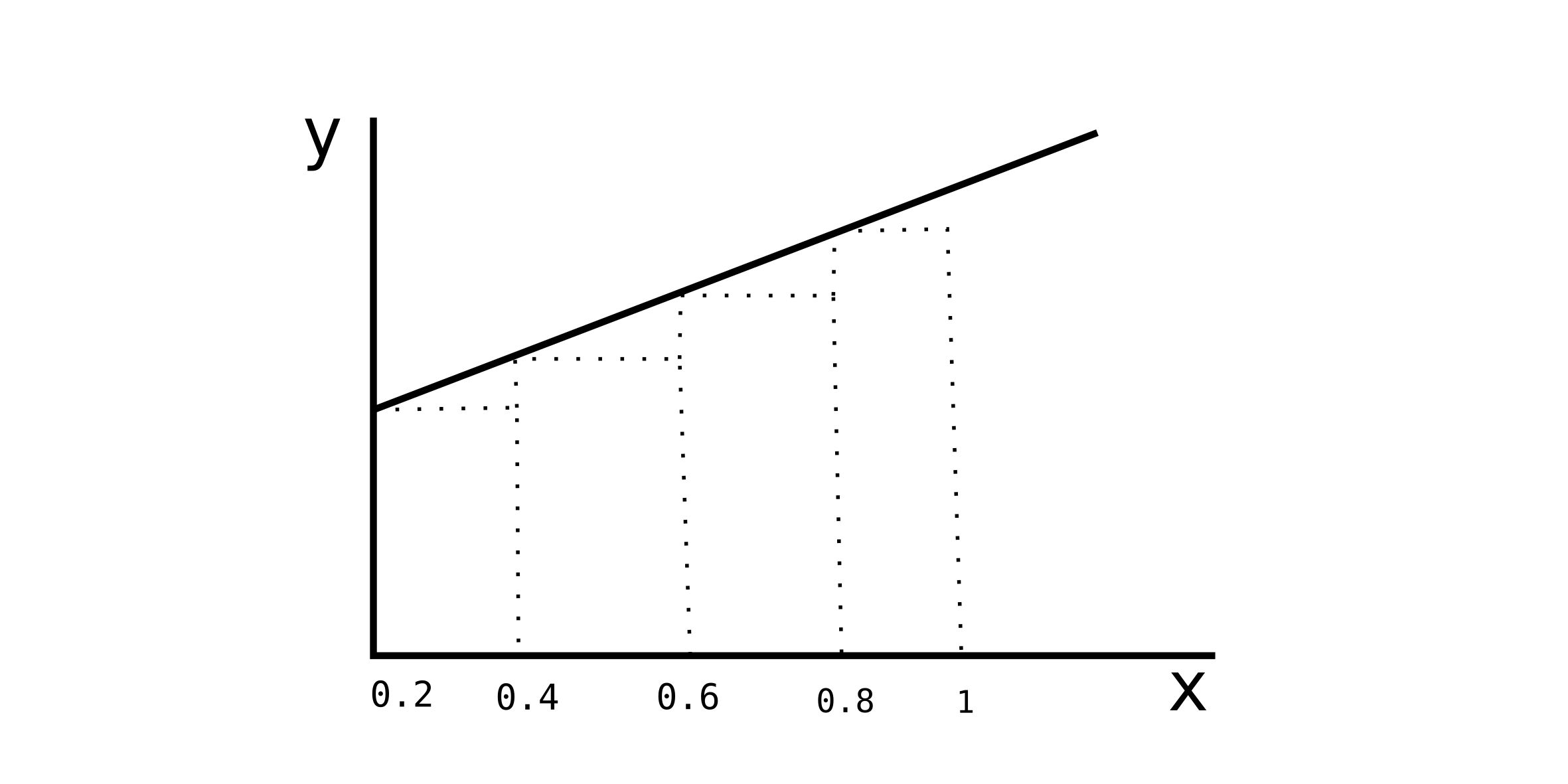
The dotted lines represent getting the Riemann Sum from the left. This is why it’s an underestimate for the area under the curve. And the right Riemann Sum would overestimate the area under a curve (because it gets the height from the right-most point).

We can consider the actual area under the curve as a trapezoid.

$A_{trap} = \frac{1}{2} (base1 + base2) h$

$= \frac{1}{2} (0.01 + 0.02) (1)$

$= 0.015$

But the geometric interpretation doesn’t always work. For example, consider $f(x) = 0.01 (1+x^2)$.

It’s also possible for our function to be negative.

In this case, the area would be negative. $height = -f (s_i)$

$\lim_{mesh \to 0} R_{P}^{S} (f) = A_2 - A_1$

2.3 The Definite Integral

Definition:

If our function is defined on the closed interval $[a, b]$ then $\lim_{\mid \mid P\mid \mid \to 0} R_{P}^{S} (f) $ is $\lim_{\mid \mid P \mid \mid \to 0} \sum_{}^{} f(s_i) \Delta x_i = L$ (the limit exists).

This is equal to $\int_{a}^{b} f(x) dx$. In this case, $f(x)$ is the integrand and a and b are the limits of integration.

What are some functions where they are not Riemann integrable?

Compare $f(x) = 0$ if $x=0$ and $f(x) = \frac{1}{x},\ 0<x\le 1$

Because this is unbounded, this is not integrable.

With $g(x) = 0,\ 0\le x\le 0.1$ and $g(x) = \frac{1}{x},\ 0.1 \le x\le 1$

Because the limit exists when we approach it from the right, it is bounded and therefore it is integrable.

We can picture the Riemann integral as the area under the curve.

And recall that the area can be negative (when the function line is below the x axis).

Consider $y=f(x) = k$

$\int_{a}^{b} k dx = k (b - a)$ (height times width of interval)

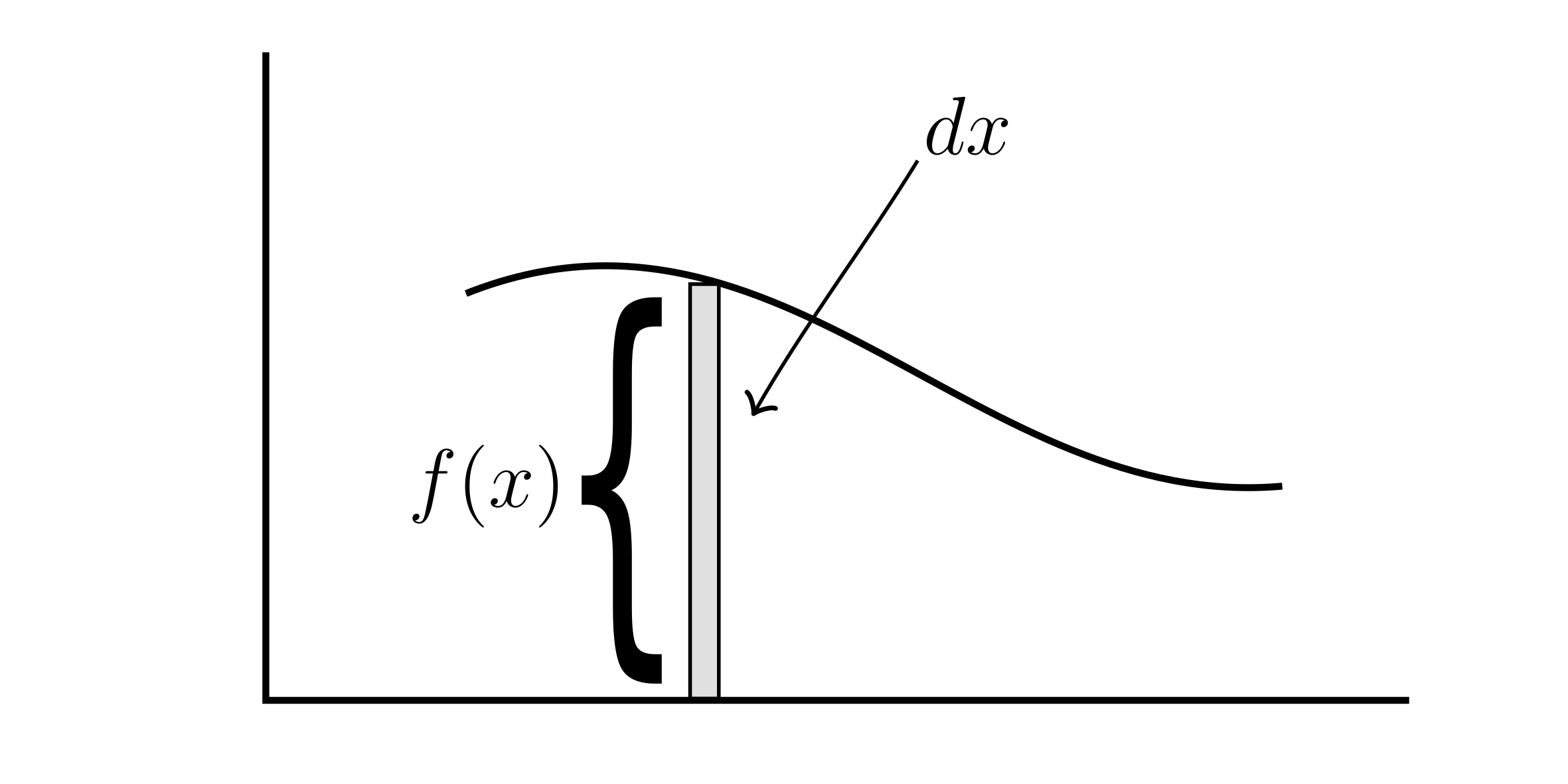
$\int_{a}^{b} f(x) dx = \lim_{\mid \mid p\mid\mid \to 0} R_{P}^{S} (f)$

$= \sum_{i=1}^{n} f(s_i) \Delta x_i$

Example:

$f(x) = 7,\ 1\le x<3$ or $3\le x\le 5$ and $f(x) = 4,\ x=3$

$\int_{1}^{5} f(x) dx = \int_{1}^{3} f(x) dx + \int_{3}^{5} f(x) dx = 7(3-1) + 7(5-3) = 28$

The point is infinitely small so it doesn’t matter.

Properties:

Addition:

$\int_{a}^{b} f(x) dx = \int_{a}^{c} f(x) dx + \int_{c}^{b} f(x) dx$

Linearity:

$\int_{a}^{b} (r f(x) + sg(x)) dx = r \int_{a}^{b} f(x) dx + s \int_{a}^{b} g(x) dx$

Monotonicity of Integration:

If $f(x) \le g(x)$

Then $\int_{a}^{b} f(x) dx \le \int_{a}^{b} g(x) dx$

Handling Absolute Value

You have to find c where f changes sign (negative to positive). $\int_{a}^{b} \mid f(x) \mid dx = \int_{a}^{c} - f(x) dx + \int_{c}^{b} f(x) dx$

Example:

Suppose we have $f(x) = x$.

We want $\int_{a}^{b} x dx$.

Divide our closed interval [a, b] into n subintervals.

$\Delta x = \frac{b-a}{n}$

$P_n = a, a+\Delta x, a+2 \Delta x, …,a+ (n-1)\Delta x, b$

We will do a right-hand Riemann Sum with $s_i = a + i \Delta x$. Therefore

$R_{P}^{R} (f) = \sum_{i=1}^{n} f(s_i) \Delta x_i$

$= \sum_{i=1}^{n} (a+i\Delta x) \Delta x$

$= \sum_{i=1}^{0} a \Delta x + \sum_{i=1}^{n} i(\Delta x)^2$

$= a \Delta x \sum_{i=1}^{n} 1 + (\Delta x)^2 \sum_{i=1}^{n} i$

$= a \Delta x n + (\Delta x)^2 \frac{n(n+1)}{2}$

$= an (\frac{b-a}{n}) + \frac{(b-a)^2}{n^2} \frac{n(n+1)}{2}$

$= a(b-a) + \frac{(b-a)^2}{2} (1+ \frac{1}{n})$

So $\int_{a}^{b} x dx = \lim_{n \to \infty} R_{P}^{R} (f) = \lim_{n \to \infty} \left(a (b-a) + \frac{(b-a)^2}{2} \left( 1 + \frac{1}{n} \right) \right)$

$= a(b-a) + \frac{(b-a)(b-a)}{2}$

$= (b-a) \left( \frac{2a}{2} + \frac{b-a}{2} \right)$

$= (b-a) \left( \frac{b-a}{2} \right)$

$\fbox{$= \frac{b^2 - a^2}{2}$ }$

Proposition:

$\int_{a}^{b} x dx = \frac{b^2}{2} - \frac{a^2}{2}$

$\int_{a}^{b} x^2 dx = \frac{b^3}{3} - \frac{a^3}{3}$

So now we know that the definite integral is the anti-derivative evaluated at the end point b minus the anti-derivative at the start point a.

Average value of a continuous function, $f$, in [a, b].

Recall average of n numbers:

$\frac{x_1 + x_2 + x_3, …, x_n}{n}$

So now,

$\frac{f(x_1) + f(x_2) + f(x_3), …, f(x_n)}{n}$

$= \frac{f(x_1) + f(x_2) + f(x_3), …, f(x_n)}{(b-a)} \Delta x$

$= \frac{1}{b-a} \sum_{i=1}^{n} f(x_i) \Delta x_i$

$= \lim_{n \to \infty} \frac{1}{b-a} \sum_{i=1}^{n} f(x_i) \Delta x_i$

$= \frac{1}{b-a} \int_{a}^{b} f(x) dx$

So $(A_f)(b-a) = \int_{a}^{b} f(x) dx$

Mean Value Theorem for Integration:

Let $f(x)$ be a continuous function on [a, b], then there exists c such that $\int_{a}^{b} f(x) dx = f(c)(b-a)$

Recall that the mean value theorem for derivatives was:

$f’(c) = \frac{f(b)-f(a)}{b-a}$

Example:

Find the average value of the function $f(x) = e^x$ on [0, 2].

$\frac{e^2 - e^0}{2} = \frac{e^2 - 1}{2} \approx 3.19$

Find c for that average value. That is, at what point on the interval does the function equal the average?

$c = \ln \left( \frac{e^2 - 1}{2} \right) \approx 1.16$

Example (#3):

$\int_{-4}^{8} (\mid n -4 \mid + 2) du$

Find some c where the function goes from negative to positive and make it into a piece-wise function.

$= \int_{-4}^{4} (- (u - 4) + 2) du + \int_{4}^{8} (u-4 + 2) du$

$= \int_{-4}^{4} - (u - 4 + 2) du + \int_{4}^{8} (u-4 + 2)$

$= \int_{-4}^{4} (-u + 6) du + \int_{4}^{8} u-2 du$

$= (\frac{-u^2}{2} + 6u)\mid _{-4}^{4} + (\frac{u^2}{2} - 2u) \mid _{4}^{8}$

$= 48 + 16 = 64$

Example (#2):

Calculate the definite integral

$\int_{-3}^{6} (5t - 7) dt$

$[\frac{5t^2}{2} - 7t]\mid _{-3}^{6} = \frac{9}{2}$

Example (#14):

Calculate the average value of $c(x) = -10$ over [-11, 9].

Average value: -10

Example (#22):

Given the velocity function, calculate the average velocity $v(t) = 3t + 2$ over [4, 8].

$= \frac{1}{b-a} \int_{a}^{b} f(x) dx$

$= \frac{1}{4} \int_{4}^{8} 3t + 2 dt$

$= \frac{1}{4} [\frac{3t^2}{2} + 2t]\mid _{4}^{8}$

$= \frac{1}{4} 80 = 20$

Example (#35):

Estimate the definite integral using the given partition and the left sample set

$\int_{0}^{1} \sqrt{x} dx$

$P = {0, \frac{1}{4}, \frac{1}{3}, \frac{3}{4}, 1}$

$\sum_{i=1}^{5} f(x_i) \Delta x_i$

$= \sqrt{0} \frac{1}{4} + \sqrt{\frac{1}{4}} \frac{1}{12} + \sqrt{\frac{1}{3}} \frac{5}{12} + \sqrt{\frac{3}{4}} \frac{1}{4}$

$\approx 0.4987$

Now, what is the exact definite integral?

$= \frac{2}{3}x^{\frac{3}{2}} \mid _{0}^{1} = \frac{2}{3}$

2.4 The Fundamental Theorem of Calculus

Theorem

Let $f$ be a continuous function on [a, b].

The function $G(x) = \int_{a}^{x} f(t) dt$ is an anti-derivative of $f$ on [a, b].
- $\left( \int_{a}^{x} f(t) dt \right)’ = G’(x) = f(x)$
- Continuous functions have anti-derivatives
If $F(x)$ is any anti-derivative of our function $f$ on [a, b], then
- $\int_{a}^{b} f(x) dx = F(x) \mid _{a}^{b} = F(b) - F(a)$

$F(x) = \int_{c}^{x} f(t) dt$

$F’(x) = f(x)$

Consider a to be to the left of x and b to be to the right of x.

$F(b) = \int_{c}^{b} f(t) dt$ $F(a) = \int_{c}^{a} f(t) dt$

So $F(b) - F(a) = \int_{c}^{b} f(t) dt - \int_{c}^{a} f(t) dt = \int_{a}^{b} f(t) dt$

If $G(x)$ and $F(x)$ are anti-derivatives of our function on [a, b], then there exists c such that $G(x) = F(x) + C$. That is, $G(x) = \int_{a}^{x} f(t) dt = F(x) + C$

Let $x=a$, then $\int_{a}^{a} f(t) dt = F(a) + C$ (Part one of theorem)

Let $x=b$, then $\int_{a}^{b} f(t) dt = F(b) + C$ (Part two of theorem)

Why is part two true?

The whole change is the sum of little changes.

Consider a function that goes from a and b.

($x_1$ is part way to b)

(The star near the x denotes some place in the interval)

$F(b) - F(a) = F(x_1) - F(x_0) + F(x_2) - F(x_1) + … + F(x_n) - F(x_{n-1}) + F(x_b) - F(x_a)$

$ = F’(x_1*) \Delta x + F’(X_2 *) \Delta x + … + F’(x_n *) \Delta x$

Change in interval = rate of change * width of interval

This now means that $F(b) - F(a) = \sum_{i=1}^{n} f(x_i *) \Delta x$ (Note that this is the Riemann Sum).

$F(b) - F(a) = \lim_{n \to \infty} \sum_{i=1}^{n} f(x_i *) \Delta x = \int_{a}^{b} f(x) dx$

Why is part one true?

$G(x) = \int_{a}^{x} f(t) dt$

We will show that $\frac{dG}{dx} = f(x)$

Suppose $f$ is continuous on [a, b]

$G(x) = \int_{a}^{x} f(t) dt$

$G(x+h) = \int_{a}^{x+h} f(t) dt$

$G(x+h) - G(x) = \int_{a}^{x+h} f(t) dt - \int_{a}^{x} ft dt = \int_{x}^{x+h} f(t) dt$

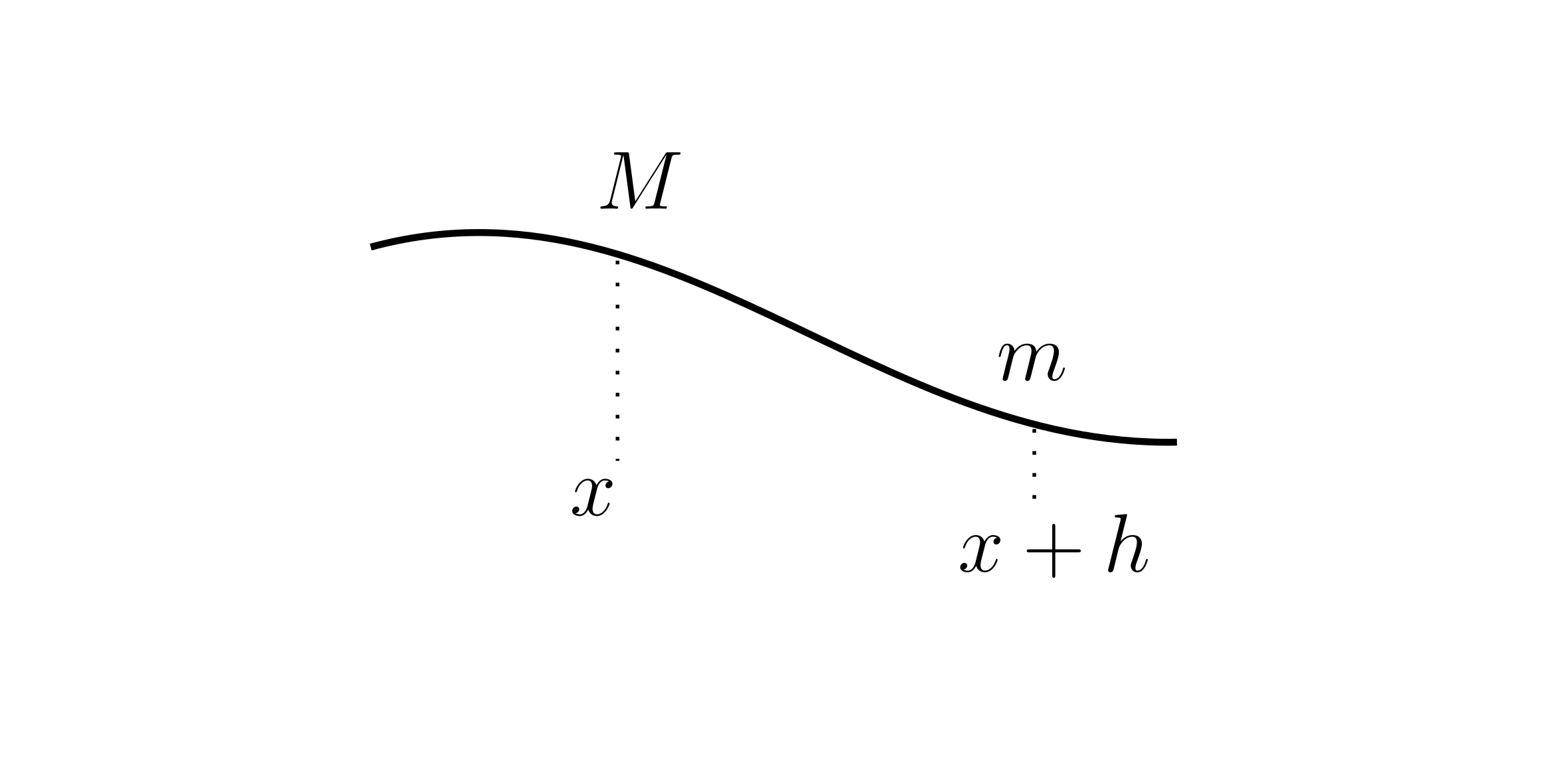
Let $M$ be a max of $f$ on [a, x+h].

Let $m$ be a min of $f$ on [a, x+h].

For some $t$ in [x, x+h]

$m \le f(t) \le M$
$mh \le \int_{x}^{x+h} f(t) dt \le Mh$
- In other words, lower rectangle <= Riemann sum <= upper rectangle

$\lim_{h \to 0} m \le \frac{1}{h} \int_{x}^{x+h} f(t) dt \le M$

$\lim_{h \to 0} m \le \frac{1}{h} (G(x+h) - G(x)) \le M$

$\lim_{h \to 0} m = \lim_{h \to 0} M = f(x)$

So $\frac{dG}{dx} = \lim_{h \to 0} \frac{1}{h} (G(x+h) - G(x)) = f(x)$

Example:

We want the area between x=1 and x=3 for $y=\frac{1}{x}$.

This is just $\int_{1}^{3} \frac{1}{x} dx = [\ln (x)]\mid _{1}^{3} = \ln (3) - 0 = \fbox{$\ln (3)$}$

Example:

Suppose $f$ is continuous on [a, b] and $G(x) = \int_{a}^{x^2} f(t) dt$. What is $\frac{dG}{dx}$?

HINT: Use Chain Rule

$G(x) = F(x^2) - F(a)$

$\frac{dG}{dx} = \frac{d}{dx}(F(x^2)) - \frac{d}{dx} F(a) = \frac{dF}{dx} 2x = \fbox{$2xf(x^2)$}$

Example:

Use the Theorem to solve $\frac{d}{dx} \int_{0}^{3x} 3t dt$

$\frac{d}{dx} \frac{3t^2}{2} \mid _{0}^{3x} = \frac{d}{dx} ( \frac{3(3x^2)}{2} - \frac{3(0^2)}{2})$

$= \frac{d}{dx} \frac{27 x^2}{2} = \fbox{$27x$}$

3.2 Area in the Plane

Suppose we want the area between $y=x-1$ and the x-axis between 0 and 2.

$\int_{0}^{2} (x-1) dx = \frac{1}{2}x^2 - x \mid _{0}^{2} = \frac{1}{2} 2^2 - 2 - 0 = 0$

This isn’t actually 0, but because $A_2$ is negative, it cancels with $A_1$.

Instead, $\int_{0}^{2} (x-1) dx = \int_{0}^{1} (x-1) dx + \int_{1}^{2} (x-1) dx = -A_2 + A_1$

So we want $\int_{0}^{2} \mid x-1 \mid dx$

Proposition:

$y=f(x)$ is a definite and integrable function on $I$ then the area between the function and the x-axis on $I$ is $\int_{a}^{b} \mid f(x) \mid dx$.

If $f(x) \ge 0$ then $\mid f(x) \mid = f(x)$

If $f(x) \le 0$ then $\mid f(x) \mid = - f(x)$

So $\int_{0}^{2} \mid x-1 \mid dx = \int_{0}^{1} - (x-1) dx + \int_{1}^{2} + (x-1) dx$

$= -(\frac{x^2}{2} - x) \mid _{0}^{1} + (\frac{x^2}{2} - x) \mid _{1}^{2}$

$= -(\frac{1}{2} - 1) - (0) + (\frac{2^2}{2} - 2) - (\frac{1}{2} - 1) = 1$

We can work with things that aren’t just the x-axis, however.

Example:

Consider $y=f(x) = x^2$ and $y=g(x) = 4$

We want the area between f and g for $1\le x\le 3$

Consider $f(x) = x^2 + e^{-x^2}$ and $g(x) = 4+e^{-x^2}$. Because these both have a constant factor, we can cancel them out.

In general, we want: $\int_{a}^{b} \mid f(x) - g(x) \mid dx$

We add up $A_1$ and $A_2$.

$A_1 = \int_{1}^{2} 4 - (x^2 - 4) dx = \int_{1}^{2} x^2 dx = \frac{x^3}{3} \mid _{1}^{2}= \frac{7}{3}$

$A_2 = \int_{2}^{3} (x^2-4) - 4 dx = \int_{2}^{3} x^2 - 8 dx = \frac{x^3}{3} - 8x \mid _{2}^{3} = \frac{5}{3}$

$A_1 + A_2 = 4$

Example:

Find the area between $y=\sin(x)$ and $y=\cos (x)$ on the interval $0\le x\le \frac{\pi}{6}$

In this interval, cos is always greater than sin.

Therefore the area is $\int_{0}^{\frac{\pi}{6}} \cos(x) - \sin(x) dx = \sin (x) + \cos(x) \mid _{0}^{\frac{\pi}{6}}$

$= \sin(\frac{\pi}{6}) + \cos(\frac{\pi}{6}) - (\sin(0) + \cos(0))$

$= \frac{1}{2} + \frac{\sqrt{3} }{2} - 0 - 1 = \fbox{$\frac{\sqrt{3} -1}{2}$}$

Going over quiz 8

$y(x) = \cos(x)$

$P = \frac{-3\pi}{2}, \frac{-\pi}{2}, \frac{\pi}{2}, \frac{3\pi}{2}$

$M = -\pi, 0, \pi$

$\Delta x = \pi$

$R^{M} _{P} (f) = \sum _{i=1}^{3} y(x) \Delta x = (\cos(-\pi) + \cos(0) + \cos(\pi))\pi = -\pi$

$s_i = \pi (i - 2)$

$h(x) = x$ $P = 0, …, 3$

$\Delta x = \frac{b-a}{n} = \frac{3}{n}$

$s_i = \frac{3i}{n}$

$R(f) = \sum^{n} _ {i=1} h(x) \Delta x_i = \sum_{i=1}^{n} \frac{3i}{n} \frac{3}{n} = \frac{9}{n^2}\sum_{i=1}^{n} i = \frac{9}{2}(1+\frac{1}{n})$

Example:

Find the area of the bounded region between $y=f(x) = x^3$ and $y=g(x)=x^2$. The bounded region is in the interval [0, 1].

In this interval, $x^2$ is always greater than $x^3$.

$\int_{0}^{1} x^2 dx - \int_{0}^{1} x^3 dx = \frac{x^3}{3} \mid _{0}^{1} - \frac{x^4}{4} \mid _{0}^{1}$

$= \frac{1}{3} - \frac{1}{4} = \fbox{$\frac{1}{12}$}$

Example:

Let $f(x) = e^{-x} + e^{x^2}$ and $g(x) = e^{-3x+4} + e^{x^2}$. Find the area between the graphs of f and g for $0\le x \le 3$

We can get rid of the similarity $e^{x^2}$ and we are left with $f(x) = e^{-x}$ and $g(x) = e^{-3x+4}$

We want $\int_{0}^{3} \mid f(x) - g(x) \mid dx = \int_{0}^{3} \mid e^{-x} - e^{-3x+4} \mid dx$

They equal each other at 2.

$\int_{0}^{2} e^{-3x+4} - e^{-x} dx + \int_{2}^{3} e^{-x} - e^{-3x+4} dx$

$= (\frac{-1}{3}e^{-3x+4} + e^{-x}) \mid _{0}^{2} + (-e^{-x} + \frac{1}{3}e^{-3x+4})\mid _{2}^{3}$

$= \frac{e^4}{3} + 4 \frac{e^{-2}}{3} + \frac{e^{-5}}{3} - e^{-3} - 1 \approx 17.3$

What if we change the bounds to be $[0, \infty]$.

Is the function integrable? How do we do it?

Yes

$\int_{0}^{\infty} e^{-x} - e^{-3x+4} dx = 1-\frac{e^4}{3}$

Example:

We want the area between $x=4-y^2$ and $x=2-y$ for $0\le y\le 2$.

They are equal at (0, 2) and (3, -1).

$\int_{0}^{2} 4-y^2 dy - \int_{0}^{2} 2-y dy$

$= [4y - \frac{y^3}{3}]\mid _{0}^{2} - [2y - \frac{y^2}{2}]\mid _{0}^{2} = \frac{10}{3}$

Three ways to solve

Solve for x. Results in a square root
Swap x and y including axes
Let y be the integration variable

Example:

Calculate the are between $x=\sin(y)$ and the y-axis for $\frac{-\pi}{4}\le y\le \frac{\pi}{2}$

$\int_{\frac{-\pi}{4}}^{\frac{\pi}{2}} \mid \cos(y) \mid dy $

$\int_{-\frac{\pi}{4}}^{0} -\sin(y) dy + \int_{0}^{\frac{\pi}{2}} \sin(y) dy $

$\cos(y) \mid _{-\frac{\pi}{4}}^{0} + (-\cos(y)) \mid _{0}^{\frac{\pi}{2}}$

$= 1 - \frac{1}{\sqrt{2}} - 0 + 1 = \fbox{$2- \frac{1}{\sqrt{2}}$}$

Example:

Find the area between $x=9-y^2$ and the y-axis on $-4\le y\le 2$.

$\int_{-4}^{2} \mid 9-y^2 \mid dy $

$\int_{-4}^{-3} -9+y^2 dy + \int_{-3}^{2} (9-y^2) dy $

$[-9y+\frac{y^3}{3}] _{-4}^{-3} + [9y-\frac{y^3}{3}] _{-3}^{2} = \frac{110}{3}$

Example:

Find the area of the bounded region between $y = \frac{10}{1+x^2}$ and $y=1-\frac{7}{1+x^2}$

They equal each other at $x=-4$ and $x=4$ and the second one is always larger

$\int_{-4}^{4} 1-\frac{7}{1+x^2} - \frac{10}{1+x^2} = [17 \tan^{-1}(x) - x] _{-4}^{4} $

$= 34\tan^{-1}(x) - 8$

Example:

$x=y^2$, $y=x^2$

$x=y^2$ $\therefore y = \sqrt{x} $

They are equal at (0, 0) and (1, 1). And $y=\sqrt{x}$ is always greater in that interval.

$\int_{0}^{1} \sqrt{x} - x^2 dx$

$= [\frac{2x^{\frac{3}{2}}}{3} - \frac{x^3}{3}] _{0}^{1}$

$= \frac{1}{3}$

MATH1341 Calculus 1 for Science and Engineering

The Class

Rates of Change and the Derivative

Average Rate of Change

Def. 1.1.9 - Secant Line

Prop 1.1.10 - Slope of Secant Line

Instantaneous Rates of Change

Def. 1.2.3 - Limit Definition of Derivative

Point-slope Form

1.3 Limits and Continuity

Theorem 1.3.15: Limit Rules

Continuity

1.4 Instantaneous Rates of Change: The Derivative

Limit Definition of the Derivative

Notation:

Propositions:

Examples:

Differentiability

1.5 Extrema and the Mean Value Theorem

Extrema

Extreme Value Theorem

Theorem 1.5.4

Examples

Mean Value Theorem

First Derivative Test for Extrema

1.6 Higher Order Derivatives

Examples

Definition - Concave

Theorem 1.6.9 - 2nd Derivative Test for Extrema

2.0 Rules for Derivative

Theorem 2.1.1 Power Rule for Natural Exponents

2.1 The Power Rule and Linearity

Topic: Summation Notation

Theorem 2.1.8 Derivative of Polynomial Summations

2.2 The Product and Quotient Rule

Power Rule for Integers

2.3 The Chain Rule

Chain Rule to Find Derivative of a Rational Power

Power Rule for Rational Powers

Inverse Functions

Inverse Function Theorem

Chain Rule for Implicit Differentiation

2.4 The Exponential Function

Properties

2.5 The Natural Logarithm

Properties

Algebraic Properties of Logs

Logarithmic Differentiation

Proving Rules Using Logarithmic Differentiation

2.6 General Exponential and Logarithmic Functions

Properties:

Second Derivative

Converting to Base e

Derivatives of Other Bases

General Power Rule

2.7 Trig Functions: Sine and Cosine

Properties

Theorem

Solutions of Differential Equations

2.8 The Other Trig Functions

Properties

Appendix A

Parameterized Curves and Motion

2.9 Inverse Trig Functions

Domains:

Derivatives

Inverse Trig Identities

3.3 Optimization

Case 1: Closed interval

Case 2: An open interval

Case 3: One critical point

3.5 L’Hopital’s Rule

4.1 What is a Differential Equation?

4.2 (or 1.2 in the new book) Anti-Derivatives

Power Rule for Integration

Linearity of Derivatives (and anti-derivatives)

Other Integration Formula:

The Chain Rule in Anti-Derivative Form (Integration by Substitution)

2.1 Sums and Differences

Sums