CS2510 Fundamentals of Computer Science 2
The Class
Fundamentals of Computer Science 1: Correct program behavior
Fundamentals of Computer Science 2: Having your code be scalable/maintainable/efficient
2% late per hour per submission for homework assignments
Read lecture notes before coming to class
Code Review: Taking your code and explain it to somebody else
- Happens towards the end of the semester
Introduction to Java
Data. We first started with atomic data.
For example:
;; a PosReal number representing the price of a coffee
(define coffee-price 3.5)
(define fancy-coffee (+ coffee-price 1.5))
(define extra-fancy-cofee (+ coffee-price "2 dollars"))
; This won't work. Can't add number to integer.
;; An Auto is a (make-auto Integar Integar String PosReal)
(define-struct auto (x y color speed))
DrRacket doesn’t know that this is wrong until you run it. Auto is an example
of compound data–meaning it holds multiple values.
Java is infix notation.
This code would not have compiled.
Java is a strongly typed language (data is checked at compile time). And ISL is dynamically typed (data is checked at run time).
Java Variables
In Java there are two types of numbers: Integers and Doubles. (There are more, but we only care about these 2 for now.)
Also, you can’t have dashes in Java’s names–instead use camelCase. Example in Java:
// Primative Types
int distance = 3;
double coffeePrice = 3.5;
String hi = "hello";
char a = 'a';
boolean isSunny = false;
Why is String capitalized? Because it is not a primitive data type.
Compound Data in Java
Example - Auto
class Auto {
//int x;
//int y;
Location loc;
String color;
double speed;
//Auto(int x, int y, String color, double speed){ // This is a constructor
Auto(Location loc, String color, double speed){
//this.x = x; // _this_ means the one in the class
//this.y = y;
this.loc = loc;
this.color = color;
this.speed = speed;
}
}
class Location{
int x;
int y;
Location(int x, int y){
this.x = x;
this.y = y;
}
}
class ExamplesAuto{
Location Loc34 = new Location(3, 4);
Auto car1 = new Auto(Loc34, "red", 50.0);
ExamplesAuto(){}
}
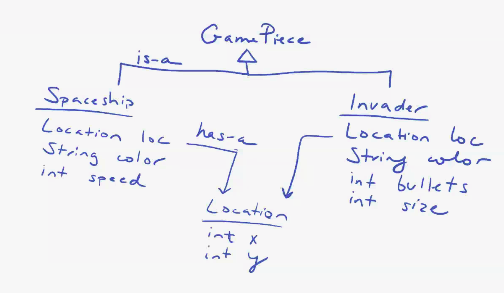
Unions
Example - Spaceships
Racket:
(define-struct invader (loc color bullets size))
;; An Invader is a (make-invader Posn String PosInt PosInt
(define invader1 (make-invader (make-posn 60 120) "green" 30 3))
#;(define (invader-temp1 inv)
(posn-temp1 (invader-loc inv))
(invader-color inv)
(invader-bullets inv)
(invader-size inv))
(define-struct ship (loc color speed))
;; A Shapeship is a (make-ship Posn String PosInt)
;; interp.: loc is a position on the Cartesian plane
;; speed is measured in miles/hour
;; A GamePiece is one of:
;; - Spaceship
;; - Invader
NOTE: The Union data type is only in comments in DrRacket. In Java, however, this is not in comments.
Java
interface IGamePiece {}
// Represents an Invader in the game
class Spaceship implements IGamePiece {
Location loc
String color;
int speed;
Spaceship(Location loc, String color, int speed){
this.loc = loc;
this.color = color;
this.speed = speed;
}
}
// Represents an Invader in the game
class Invader implements IGamePiece {
Location loc
String color;
int bullets;
int size;
Invader(Location loc, String color, int bullets, int size){
this.loc = loc;
this.color = color;
this.bullets = bullets;
this.size = size;
}
}
// A class to represent a location on the Cartesian plane
class Location {
int x;
int y;
Location(int x, int y){
this.x = x;
this.y = y;
}
}
class Examples {
// You cant do the line below because it doesn't know what loc1 is yet
//Spaceship ship = new Spaceship(this.loc1, "blue", 55);
Location loc1 = new Location(30, 40);
Location loc2 = new Location(60, 80);
// Represents two IGamePieces: Spaceships and Invaders
IGamePiece ship = new Spaceship(this.loc1, "blue", 55);
IGamePiece invader1 = new Invader(this.loc2, "pink", 30, 3);
// You can still do this, but it's bad practice
//Spaceship ship = new Spaceship(new Location(30, 40), "blue", 55);
}
IGamePiece is the type at compile time
Spaceship/Invader is the type at run-time
Use the this keyword anytime you can–it removes ambiguity.
In Java, Unions are interfaces. The reason we would want to declare a variable by it’s Union is so it can be that type–which means that we can use more general operations.
Example - Ancestor Tree
Racket:
;; A Person is a (make-person String Person Person)
(define-struct person (name mom dad))
(define alice (make-person "Alice"
(make-person "Sally"
(make-person "Abby"
...
; this issue with this definition is that you cannot stop--you need a base case
; for referential data
;; An AT is one of:
;; - #false
;; - (make-person String AT AT)
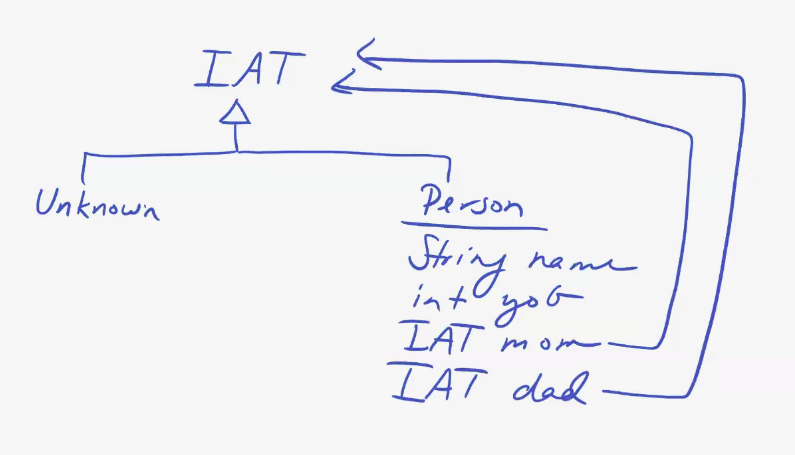
Java:
interface IAT{}
// Class to represent an unknown in an ancestor tree
class Unknown implements IAT {
Unknown() {}
}
// Class to represent a person in an ancestor tree
class Person implements IAT {
String name;
int yob
IAT mom;
IAT dad;
Person(String name, int yob, IAT mom, IAT dad) {
this.name = name;
this.yob = yob;
this.mom = mom;
this.dad = dad;
}
}
Methods
Recall the design recipe for functions:
- Signature
- Purpose Statement
- Examples/Tests
- Code
- Run
Consider the DrRacket code:
;; Spaceship Integer -> Integer
;; produces a reduced speed for the given spaceship based on a given percentage
(check-expect (reduced-speed ship1 20) 80) ; ship1 has a speed of 100
(check-expect (reduced-speed ship2 50) 25) ; ship2 has a speed of 25
(define (reduced-speed ship rate)
(- (ship-speed ship) (/ (* (ship-speed ship) rate) 100)))
Template
What do I have to work with?
You have to do a template for each class
- If a method takes in a complex data type, you need another template: ```java /* everything in template above plus
- fields:
- …
- methods:
- …
- methods for fields:
- … ```
In Java, we just list the things:
import tester.*;
interface IGamePiece {
//moves this IGamePiece by the given x and y
IGamePiece move(int x, int y); //tells the program that every GamePiece has this method
}
// Represents an Invader in the game
class Invader implements IGamePiece {
Location loc
String color;
int bullets;
int size;
Invader(Location loc, String color, int bullets, int size){
this.loc = loc;
this.color = color;
this.bullets = bullets;
this.size = size;
}
/* TEMPLATE HERE
*
*/
public IGamePice move(int x, int y){
return new Invader(this.loc.move(x, y), this.color, this.bullets, this.size);
}
}
// Represents an Spaceship in the game
class Spaceship implements IGamePiece {
Location loc;
String color;
int speed; //in miles per hour
Spaceship(Location loc, String color, int speed) {
this.loc = loc;
this.color = color;
this.speed = speed;
}
/* fields:
* this.local ... Location
* this.color ... String
* this.speed ... int
* methods:
* this.reducedSpeed(int) ... int
* this.move(int, int) ... Spaceship
* methods for fields:
* this.loc.moveLocation(int, int) ... Location
*/
// produces a reduced speed for this spaceship based on the given percentage
int reducedSpeed(int rate) {
return this.speed - ((this.speed * rate) / 100);
}
// produces a new spaceship that is shifted from this spaceship by the given x and y
Spaceship move(int x, int y){
return new Spaceship(this.loc.move(x,y), this.color, this.speed);
}
}
class Location {
int x;
int y;
Location(int x, int y){
this.x = x;
this.y = y;
}
/* fields
* this.x ... int
* this.y ... int
* methods:
* this.moveLocation(int, int) ... Location
*/
//Create a new Location that is shifted from this location by a given x and y
Location move(int x, int y){
return new Location(this.x + x, this.y + y);
}
}
class Examples {
Location loc1 = new Location(30, 40);
Location loc2 = new Location(60, 80);
Spaceship ship1 = new Spaceship(this.loc1, "blue", 100);
Spaceship ship1 = new Spaceship(this.loc2, "pink", 30);
//tests for reducing speed
boolean testReducedSpeed(Tester t) { //these test methods need to start with the word `test`
return t.checkExpect(this.ship1.reducedSpeed(20), 80) &&
t.checkExpect(this.ship2.reducedSpeed(50), 15);
}
//tests for move
boolean testMove(Tester t){
return t.checkExpect(this.ship1.move(1, 2),
new Spaceship(new Location(31, 42), "blue", "100")) &&
t.checkExpect(this.loc1.moveLocation(2, 3), new Location(32, 43));
}
//tests for move
boolean testMove(Test t){
return t.checkExpect(this.ship1.move(10, 20),
new Spaceship(new Location(40, 60), "blue", 55));
//notice that we never ask if something is a Spaceship
}
Methods for Unions
We can use the color class by importing the image library.
Incorrect:
import java.awt.Color
import javalib.worldimages.*
//...
//In Spaceship class
WorldImage draw() {
return new CircleImage(50, "solid", this.color)
}
// in Examples class
IGamePiece ship1 = new Spaceship(this.loc1, Color.BLUE, 55);
this.ship.draw()
// this wouldn't work because draw is in the Spaceship class, NOT IGamePice (which ship1 is)
So in this case, you would want to put draw() in the interface (not just the ship class).
Correct:
import java.awt.Color;
import javalib.worldimages.*;
interface IGamePice {
//...
WorldImage draw();
}
//...
//in spaceship class
public WorldImage draw() {
return new EllipseImage(50, 60, "solid", this.color);
}
//In invader class
public WorldImage draw() {
return new ...
}
Example - Shape
interface IShape {
double area();
boolean biggerThan(IShape that);
}
class Circle implements IShape {
CartPt center;
int radius;
String color;
Circle(CartPt center, int radius, String color){
this.center = center;
this.radius = radius;
this.color = color;
}
/*
// ** TEMPLATE **
public returnType methodName() {
... this.center ... -- CartPt
... this.radius ... -- int
... this.color ... -- String
... this.area() ... -- double
... this.distToOrigin() ... -- double
... this.grow(int inc) ... -- IShape
... this.biggerThan(IShape that) ... -- boolean
... this.contains(CartPt pt) ... -- boolean
*/
// See Lecture code for all of these methods
public double area(){
return Math.PI * Math.pow(this.radius, 2);
}
public boolean biggerThan(IShape that){
return this.area() > that.area();
}
}
class Square implements IShape {
CartPt nw;
int size;
String color;
Square(CartPt nw, int size, String color) {
this.nw = nw;
this.size = size;
this.color = color;
}
/*
// ** TEMPLATE **
returnType methodName() {
... this.nw ... -- CartPt
... this.size ... -- int
... this.color ... -- String
... this.area() ... -- double
... this.distToOrigin() ... -- double
... this.grow(int inc) ... -- IShape
}
*/
// to compute the area of this shape
public double area(){
return this.size * this.size;
}
public boolean biggerThan(IShape that){
/* everything in the Circle template plus:
* fields of that:
*
* methods of that:
* that.area() ... double
*/
return this.area() > that.area();
}
}
class CartPt {
int x;
int y;
CartPt(int x, int y) {
this.x = x;
this.y = y;
}
// to compute the distance form this point to the origin
public double distToOrigin(){
return Math.sqrt(this.x * this.x + this.y * this.y);
}
// to compute the distance form this point to the given point
public double distTo(CartPt pt){
return Math.sqrt((this.x - pt.x) * (this.x - pt.x) +
(this.y - pt.y) * (this.y - pt.y));
}
}
You can also nest interfaces:
class Combo implements IShape {
IShape top;
IShape bottom;
Combo(IShape top, Ishape bottom) {
this.top = top;
this.bottom = bottom;
}
/* fields:
* this.top ... IShape
* this.bottom ... IShape
* methods:
* this.area() ... double
* this.biggerThan(IShape) ... boolean
* methods for fields:
* this.top.area() ... double
* this.bottom.area() ... double
* this.top.biggerThan(IShape) ... boolean
* this.bottom.biggerThan(IShape) ... boolean
*/
public double area() {
return this.top.area() + this.bottom.area();
}
public double biggerThan(IShape that){
return this.area() > that.area();
}
}
class ExamplesShapes{
IShape combo1 = new Combo(this.c1, this.s1); //both c1 and s1 are IShapes
IShape combo2 = new Combo(this.combo1, this.combo1);
}
Methods for Self-referential lists
Recall list of numbers from Fundies 1:
;; A [List-of Number] is one of:
;; - '()
;; - (cons Number [List-of Number])
Notice the self-referential nature of this.
Example - List of Integers
interface ILoInteger{}
class MtLoInteger implements ILoInteger {}
// By not having a constructor, it has the 'default' constructor which is nothing
class ConsLoInteger implements ILoInteger {
int first;
ILoInteger rest;
ConsLoInteger(int first, ILoInteger rest) {
this.first = first;
this.rest = rest;
}
}
Recall the template from Fundies 1:
(define (Lon-temp alon)
(cond [(empty? alon) ... ]
[(cons? alon) ... (first alon)...
(lon-temp (rest alon)) ...]))
Example - Painting
interface ILoPainting {
//count the paintings in this list
int count();
//get the paintings in this list that are by the artist with the given name
ILoPainting getByArtist(String name) {}
}
class MtLoPainting implements ILoPainting {
/*
methods:
*/
// count the paintings in this MtLoPainting
public int count(){
return 0;
}
ILoPainting getByArtist(String name){
return this;
}
}
class ConsLoPainting implements ILoPainting {
Painting first;
ILoPainting rest;
ConsLoPainting(Paining first, ILoPainting rest) {
this.first = first;
this.rest = rest;
}
/* fields:
this.first ... Painting
this.rest ... ILoPainting
Methods:
this.count() ... int
Methods for fields:
this.rest.count() ... Int
this.rest.getByArtist(String) ... ILoPainting
*/
public int count() {
return 1 + this.rest.count();
}
ILoPainting getByArtist(String name) {
if (this.first.getName(name)){
return new ConsLoPainting(this.first, this.rest.getByArtist(name));
}
else {
return this.rest.getByArtist(name);
}
}
}
class Painting {
Artist artist;
String title;
double price; // price in millions of dollars
int year;
Painting(Artist artist, String title, int price, int year) {
this.artist = artist;
this.title = title;
this.price = price;
this.year = year;
}
/* fields:
this.artist ... Artist
this.title ... String
this.price ... Int
this.year ... Int
methods:
this.count() ... int
this.getByArtist(String) ... ILoPainting
methods for fieds:
this.artist.checkArtistName(String) ... boolean
*/
//is the name of the artist of this Painting the same as the given one?
boolean checkName(String name) {
return this.artist.checkArtistName(name);
}
}
class Artist {
String name;
int yob;
Artist(String name, int yob) {
this.name = name;
this.yob = yob;
}
/* fields
this.name ... String
this.yob ... int
methods:
this.checkArtistName(String) ... boolean
*/
//is this artist's name the same as the given one?
boolean checkArtistName(String name) {
return this.name.equals(name);
}
}
class Examples {
...
ILoPainting mt = new MtLoPainting();
ILoPainting list1 = new ConsLoPainting(this.mona, this.mt);
ILoPainting list2 =new ConsLoPainting(this.sunflowers, list1);
}
If Statement
if (true-or-false-question) {
runs if true
}
//the rest is optional
else {
runs if false
}
Insertion Sort
//in interface:
ILoPainting sortByYear();
//inserts the given painting into this sorted list
ILoPainting insertByYear(Painting p);
// in empty list
public ILoPainting sortByYear() {
return this;
}
public ILoPainting insertByYear(Painting p) {
return new ConsLoPainting(p, this);
}
// in ConsLoPainting
public ILoPainting sortByYear() {
return this.rest.sortByYear().insertByYear(this.first);
}
//insert the painting into this sorted list,
//list remains sorted after exiting the method
public ILoPainting insertByYear(Painting p) {
if (this.p.paintedBefore(first)) {
return new ConsLoPainting(p, this);
}
else {
return new ConsLoPainting(this.first, this.rest.insertByYear(p));
}
}
// in Painting
boolean paintedBefore(Painting p) {
return this.year < p.year;
}
// in examples
boolean testSort(Tester t) {
return t.checkExpect(this.list2.sortByYear(),
new ConsLoPainting(this.mona,
new ConsLoPainting(this.sunflowers, this.mt)));
}
Accumulator Methods
When to use an accumulator:
- What information do you need to keep track of? Add a parameter
- What is the starting information? Remember it
- How does the function accumulate knowledge? Is it
+,cons, selector? - How do you use the accumulator? Wrapped in a local – or helper – and initialized with starting information
Example - List of Strings
interface ILoString {
//concatenate the strings in this list in reverse order
String reverseConcat();
//helps to reverse concatenate this list
//accumulator: reversed concatenated string so far
String reverseConcatAcc(String acc);
}
class MtLoString implements ILoString {
//concatenate the strings in this list in reverse order
String reverseConcat(){
return "";
}
//helps to reverse concatenate this list
//accumulator: reversed concatenated string so far
String reverseConcatAcc(String acc) {
return acc;
}
}
class ConsLoString implements ILoString {
String first;
ILoString rest;
ConsLoString(String first, ILoString rest) {
this.first = first;
this.rest = rest;
}
//concatenate the strings in this list in reverse order
String reverseConcat() {
return this.reverseConcatAcc("");
}
//helps to reverse concatenate this list
//accumulator: reversed concatenated string so far
String reverseConcatAcc(String acc) {
return this.rest.reverseConcatAcc(this.first + " " + acc);
}
}
Example - IAT
interface IAT {
//list the names in this tree
ILoString names();
//helps accumulate the names on the dad's side of the tree
//accumulator: keeps track of the names on the dad's side
ILoString namesAcc(ILoString acc);
//is this tree well-formed?
boolean wellFormed();
//help to check if this tree is well-formed
//accumulator: keeps track of the child's year of birth
boolean wellFormedHelp(int childYob);
//produce the IAT that is younger between this IAT and a given one
IAT youngerIAT(IAT other);
//produce the IAT that is younger between this IAT and a given one
IAT youngerIATHelp(IAT other, int yob);
}
class Unknown implements IAT {
Unknown() {}
public ILoString names() {
return new MtLoString();
}
public ILoString namesAcc(ILoString acc){
return acc;
}
boolean wellFormed() {
return true;
}
boolean wellFormedHelp(int childYob) {
return true;
}
public youngerIAT(IAT other) {
return other;
}
public IAT youngerIATHelp(IAT other, int yob){
return other;
}
}
class Person implements IAT {
String name;
int yob;
IAT mom;
IAT dad;
Person(String name, int yob, IAT mom, IAT dad) {
this.name = name;
this.yob = yob;
this.mom = mom;
this.dad = dad;
}
public ILoString names() {
return this.namesAcc(new MtLoString());
}
public ILoString namesAcc(ILoString acc){
return new ConsLoString(this.name, this.mom.names(this.dad.names(acc)));
}
boolean wellFormed() {
return this.mom.wellFormedHelp(this.yob) &&
this.dad.wellFormedHelp(this.yob);
}
boolean wellFormedHelp(int childYob) {
return this.yob < childYob &&
this.mom.wellFormed(this.yob) &&
this.dad.wellFormed(this.yob);
}
public youngerIAT(IAT other) {
return other.youngerIATHelp(this, this.yob); //you don't have to ask what other is
}
public IAT youngerIATHelp(IAT other, int year){
if(this.yob > year) {
return this;
} else {
return other;
}
}
}
Another way to do this problem is to append the father list and the mother list before putting them into the consLoString:
public ILoString names2() {
return new ConsLoString(this.name, this.mom.names2().append(this.dad.names2()));
}
Practice Design
See Lecture 8 for the problems.
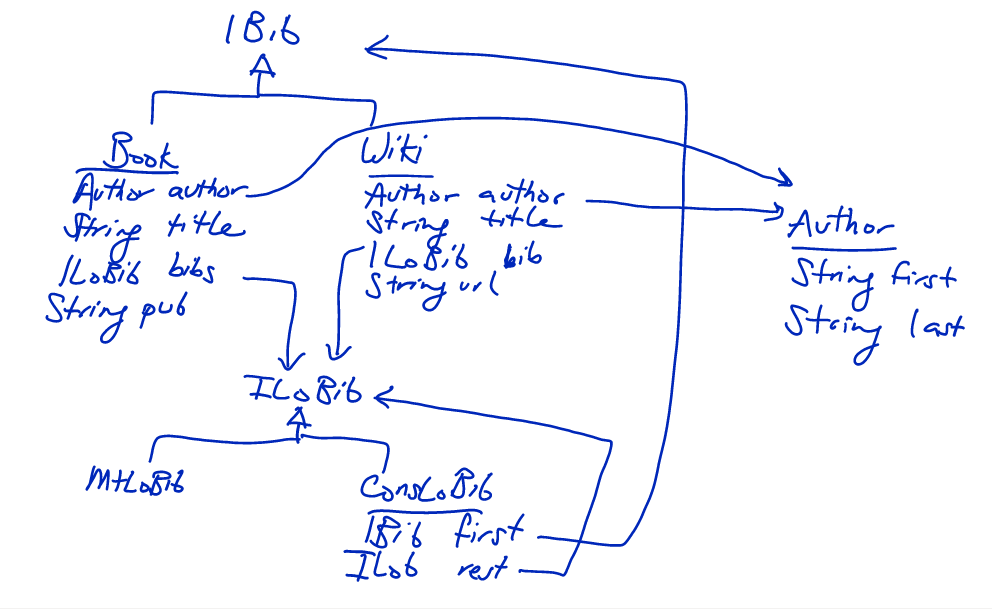
class Author {
String first;
String last;
Author(String first, String last) {
this.first = first;
this.last = last;
}
String getBib() {
return this.last + ", " + this.first + ".";
}
}
interface IBib {
ILoString sources();
}
class Book implements IBib {
Author author;
String title;
String publisher;
ILoBib bibs;
Book(Author author, String title, String publisher, ILoBib bibs) {
this.author = author;
this.title = title;
this.bibs = bibs;
this.publisher = publisher;
}
public ILoString sources() {
return new ConsLoString(this.author.getBib() + "\"" + this.title + "\"", this.bibs.sourcesFromList());
}
}
class wikiArticles implements IBib {
Author author;
String title;
String url;
ILoBib bibs;
wikiArticles(Author author, String title, String url, ILoBib bibs) {
this.author = author;
this.title = title;
this.url = url;
this.bibs = bibs;
}
public ILoString sources() {
return this.bibs.sourcesFromList();
}
}
interface ILoString {
ILoString append(ILoString other);
}
class MtLoString implements ILoString {
public ILoString append(ILoString other) {
return other;
}
}
class ConsLoString implements ILoString {
String first;
ILoString rest;
ConsLoString(String first, ILoString rest) {
this.first = first;
this.rest = rest;
}
public ILoString append(ILoString other) {
return null; // TODO: See previous lectures for append method
}
}
interface ILoBib {
ILoString sourcesFromList();}
class MtLoBib implements ILoBib {
public ILoString sourcesFromList() {
return new MtLoString();
}
}
class ConsLoBib implements ILoBib{
IBib first;
ILoBib rest;
ConsLoBib(IBib first, ILoBib rest){
this.first = first;
this.rest = rest;
}
public ILoString sourcesFromList() {
//return new ConsLoString(this.first.sources(), this.rest.sourcesFromList());
return this.first.sources().append(this.rest.sourcesFromList());
}
}
Problem 2 variant A
See if a given List has all of these requirements:
- A number that is even
- A number that is positive and odd
- A number between 5 and 10, inclusive
interface ILoInt {
//checks if this list satisfies the three requirements
boolean satisfies();
//helps check if the list satisfies the requirements
// aaccumulators: keeps track of whether each requirement was satisfied
boolean satisfiesAcc(boolean even, boolean odd, boolean bet5and10);
}
class MtLoInt implements ILoInt {
public boolean satisfies() {
return false;
}
public boolean satisfiesAcc(boolean even, boolean odd, boolean bet5and10) {
return even && odd && bet5and10;
}
}
class ConsLoInt implements ILoInt {
int first;
ILoInt rest;
ConsLoInt(int first, ILoInt rest) {
this.first = first;
this.rest = rest;
}
public boolean satisfies() {
return satisfiesAcc(false, false, false);
}
public boolean satisfiesAcc(boolean even, boolean odd, boolean bet5and10) {
return (even && odd && bet5and10) ||
(this.rest.satisfiesAcc(even || this.first % 2 == 0,
odd || (this.first % 2 == 1 && this.first > 0),
bet5and10 || (this.first >= 5 && this.first <= 10)));
}
}
class Examples {
}
If you are working with booleans, you don’t need an if statement.
Working with Images
WorldCanvas c = new WorldCanvas(300, 500);
WorldImage img1 = this.ship2.draw();
WorldImage img2 = new VisiblePinholeImage(img1).movePinholeTo(new Posn(20, 0));
img 2 new OverlayImage(new RectangleImage(30, 30, "solid", color.Black), img2);
WorldScene s = new WorldScene(300, 500), placeImageXY(img3, 150, 150);
Abstract Classes and Inheritance
Consider our IShape definition:
Remember that the Square and Circle classes have similarities.
For example: CartPt center, String color
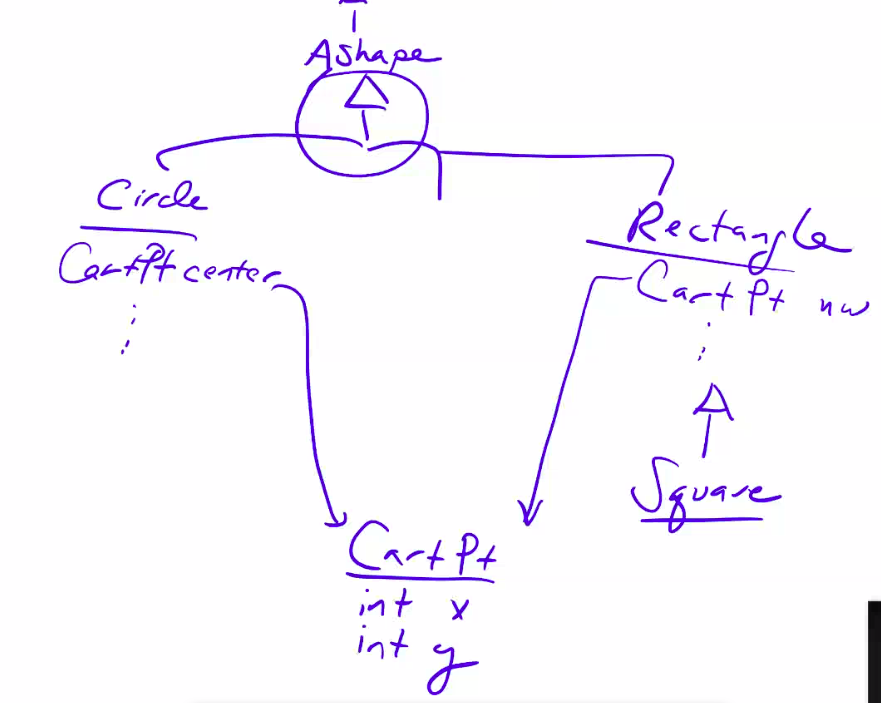
NOTE: There is IShape above AShape
//underneath IShape
abstract class AShape implements IShape{
CartPt location;
String color;
AShape(CartPt location, String color) {
this.location = location;
this.color = color;
}
//compuete the area of this AShape
public abstract double area();
public double distToOrigin() {
return this.location.distToOrigin();
}
public boolean biggerThan(IShape other) {
return this.area() >= other.area();
}
}
class Circle extends AShape {
int radius;
Circle(CartPt center, int radius, String color) {
super(center, color);
this.radius = radius;
}
public double distToOrigin() { //overriding the one in parent class
return this.location.distToOrigin() - this.radius;
}
}
class Rect extends AShape {
int width;
int height;
Rect(CartPt nw, int width, int height, String color) {
super(nw, color);
this.width = width;
this.height = height;
}
}
class Square extends Rect {
Square(CartPt nw, int size, String color) {
super(nw, size, size, color);
}
}
The extends means that it inherits everything from AShape. And because AShape implements IShape, so does Circle, Square, and Recte.
You cannot make instances of AShape (because it is abstract).
You need to say super(VARS) to send the parameters to the constructor.
You need templates for abstract classes.
You can extend classes that aren’t abstract.
You can override abstract classes
- It runs the most local method
Why have an abstract class and an interface?
It’s going to make our code more flexible when we want to add more things to our IShapes.
Should a Combo shape be AShape?
No; it doesn’t have location or color.
Customizing Constructors for Correctness and Convenience
Overriding
abstract class A {
int foo() { return 0;}
}
class B extends A {
public int foo() { return 1;}
}
Overloading
class A {
String hi() {
return "hello";
}
String hi(String name) {
return "hello, " + name;
}
Recall IGamePiece.
...
interface IGamePiece {
//Constant for the starting position
Location START_LOCATION = new Location(150, 0);
...
}
abstract class AGamePiece implements IGamePiece {
Location loc;
Color color;
AGamePiece(Location loc, Color color) {
this.loc = loc;
this.color = color;
}
// Overloading
AGamePiece(Color color) {
this(START_LOCATION, color);
}
}
class Invader extends AGamePiece {
int bullets;
int size;
Invader(Location loc, Color color, int bullets, int size) {
super(loc, color);
this.bullets = bullets;
this.size = size;
}
//Overloading
Invader(Color color, int b, int s) {
super(color);
this.bullets = b;
this.size = s;
}
...
}
class Spaceship extends AGamePiece {
int speed;
Spaceship(Location loc, Color color, int speed) {
super(loc, color);
this.speed = speed;
}
Spaceship(Color color, int speed) {
super(color);
this.speed = speed;
}
}
...
How do you call one constructor using another?
Use this. Ex: this(c, l).
What is overloading?
Its when you have two methods have the same name but different parameters.
Rules for Classes
class Date {
int month;
int day;
int year;
//constructor for data integrity
Date(int m, int d, int y) {
Utils u = new Utils();
this.month = u.checkRange(m, 1, 12, "Month is invalid");
this.day = u.checkRange(d, 1, 31, "Day is invalid");
this.year = u.checkRange(y, 1900, 2050, "Year is invalid");
}
// constructor for convenience
Date(int m, int d) {
this(m, d, 2021);
}
}
class Utils {
// Checks that the given int is within some range
int checkRange(int n, int low, int high, String message) {
if (n <= high && n >= low) {
return n;
} else {
throw new IllegalArgumentException(message);
}
}
class ExamplesDates {
Date today = new Date(2, 10, 2021);
Date lastChristmas = new Date(12, 25, 2020);
// This shouldn't be allowed
// Date badDate = new Date(-12, 120, 2);
boolean testDates(Tester t) {
return t.checkConstructorExceptions(new IllegalArgumentException("Month is invalid"),
"Date", -3, 120, 5000) &&
t.checkException(new IllegialArgumentException("nope"),
new Utils(), "checkRange", 30, 10, 2, "nope");
}
}
Defining Sameness for Complex Data
Properties of Sameness
- Reflexivity -
Ais the same asA - Symmetry - if
Ais the same asB, thenBis the same asA. - Transitivity - if
Ais the same asBandBis the same asC, thenAis the same asC. - Totality - comparing any two objects of the same type should get the correct answer
Primitive Data:
Ints:
int x = 1;
int y = 2;
x == y //False
Doubles:
double w = 1.5;
double z = 1.5;
w - z <= 0.0001 // Close enough
Booleans:
boolean t = true;
boolean s = false;
t == s
Strings (not actually primitive):
String c = "hi";
String d = "hi";
c.equals(d);
What about for complex data?
Consider a Circle from IShape.
// in circle class
boolean sameCircle(Circle that) {
return this.radius == that.radius &&
this.color.equals(that.color) &&
this.location.sameLocation(that.location);
}
// in location class
boolean sameLocation(Location that) {
return this.x == that.x &&
this.y == that.y;
}
// in examples
return t.checkExpect(this.c1.sameCircle(c2), false);
// but at compile time, these are both IShape and not circles.
We want to be able to compare two IShapes.
We need to cast it. And we need type checkers so we don’t cast a random thing as a circle.
// in circle
public boolean sameShape(IShape that) {
if (that instanceof Circle) {
return this.sameCircle((Circle) that);
} else {
return false;
}
}
// in examples
return t.checkExpect(this.c1.sameShape(c2), false) &&
t.checkExpect(this.c1.sameShape(c1), true) &&
t.checkExpect(this.c1.sameShape(r1), false);
instanceof follows the “is-a” arrows
- c1 instance of Circle -> true
- c1 instance of Rect -> false
- c1 instance of IShape -> true
- c1 instance of AShape -> true
instanceof returns true too often
- square instance of rect -> true
- rect instance of square -> false
Violates the law of symmetry
How can we get around this?
- Make our own type checkers
//in abstract class
public boolean isCircle() { return false; }
public boolean isRect() { return false; }
public boolean isSquare() { return false; }
public boolean sameCircle(Circle that) { return false; }
public boolean sameRect(Rect that) { return false; }
public boolean sameSquare(Square that) { return false; }
And just override it once in each class.
Double dynamic dispatch:
// in circle class
public boolean sameShape(IShape that) {
return that.sameCircle(this);
}
// in combo class
public booleam sameCombo(Combo that) {
return this.top.sameShape(that.top) &&
this.bot.sameShape(that.bot);
}
Another example:
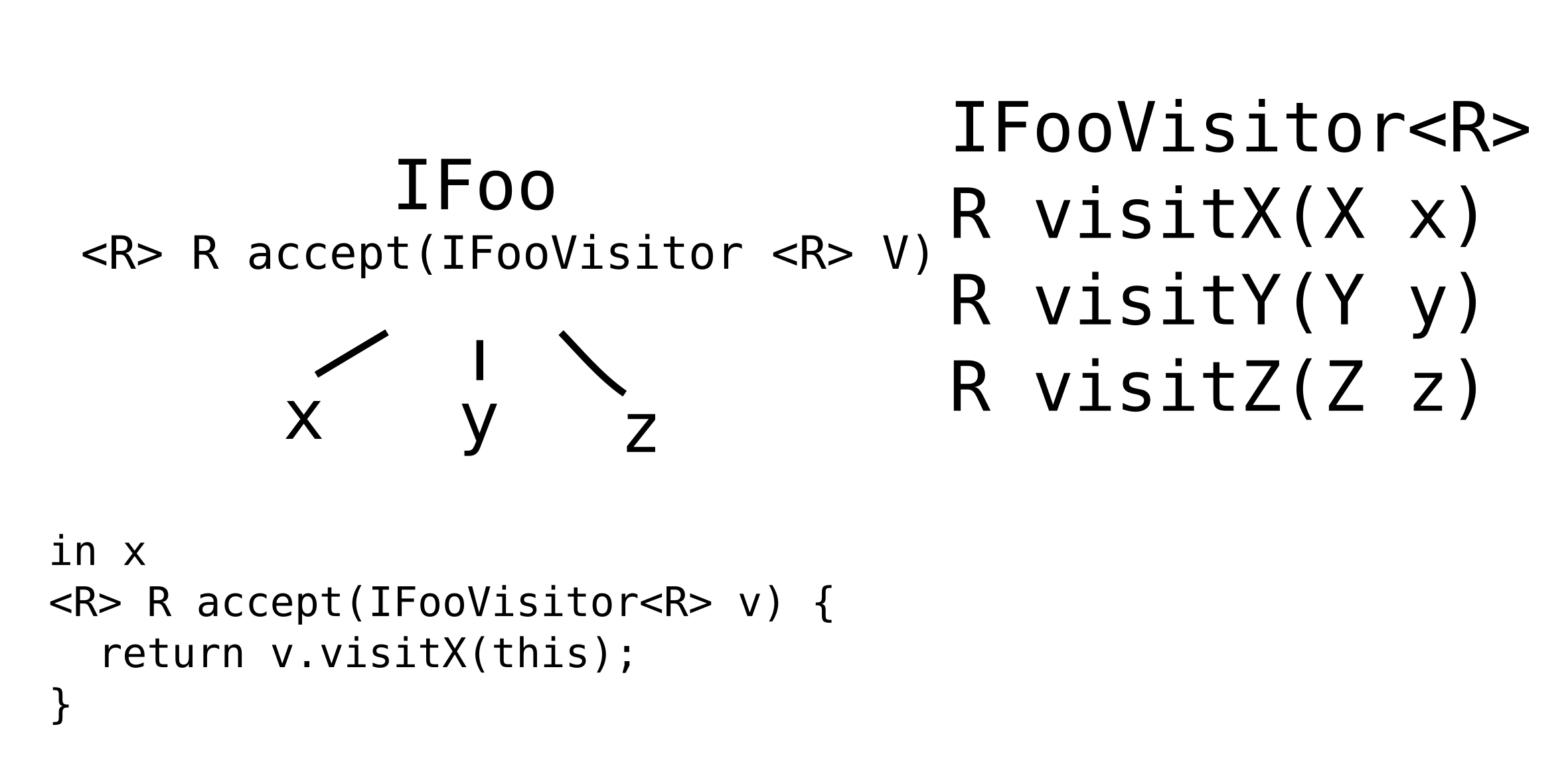
//in IFoo
boolean sameFoo(IFoo that)
boolean sameX(X that)
boolean sameY(Y that)
boolean sameZ(Z that)
// in AFoo
boolean sameX(X that) { return false; }
boolean sameY(Y that) { return false; }
boolean sameZ(Z that) { return false; }
// in X:
boolean someFoo(IFoo that) {
return that.sameX(this);
}
boolean sameX(X that) {
return ... this.field == that.field ...; //compare all fields
}
// the same for the rest of the classes
Sameness for Lists
interface ILoInt {
// is this ILoInt the same as the given one?
boolean sameLoInt(ILoInt that);
// is this ILoInt the same as the given ConsLoInt?
boolean sameCons(ConsLoInt that);
// is this ILoInt the same as the given MtLoInt?
boolean sameMt(MtLoInt that);
}
class MtLoInt implements ILoInt {
// is this ILoInt the same as the given one?
boolean sameLoInt(ILoInt that) {
return that.sameMt(this);
}
boolean sameCons(ConsLoInt that) {
return false;
}
boolean sameMt(MtLoInt that) {
return true;
}
}
class ConsLoInt implemneets ILoInt {
// is this ILoInt the same as the given one?
boolean sameLoInt(ILoInt that) {
return that.sameCons(this);
}
boolean sameCons(ConsLoInt that) {
return this.first == that.first
&& this.rest.sameLoInt(that.rest);
}
boolean sameMt(MtLoInt that) {
return false;
}
}
Exam 1
Thursday the 25th
- No lecture on the 25th
3 hours long
Will be open on Canvas from 6pm-11:59pm
Cover material from Lecture 1-Lecture 12 inclusive
Sample exam will be on Piazza today
Review is part of lab on Tuesday
Abstracting over Behavior
Recall getAllDaVinci() in the paining example.
interface ILoPainting {
// get all the painting that were painted before 1900
ILoPainting getAllBefore1900()
}
class MtLoPainting implements ILoPainting {
ILoPainting getAllBefore1900() {
return this;
}
}
class ConsLoPainting implements ILoPainting {
ILoPainting getAllDaVinci() {
if (this.first.checkArtist("DaVinci")) {
return new ConsLoPainting(this.first, this.rest.getAllDaVinci());
} else {
return this.rest.getAllDaVinci();
}
}
ILoPainting getAllBefore1900() {
if (this.first.paintedBefore1900()) {
return new ConsLoPainting(this.first, this.rest.getAllBefore1900());
} else {
return this.rest.getAllBefore1900();
}
}
}
class Painting {
Artist artist
String title
double value; // in millions of dollars
int year;
//...
boolean paintedBefore1900() {
return this.year < 1900;
}
boolean checkArtist(String name) {
return this.artist.checkName(name);
}
}
class Artist {
String name;
int yob;
//...
boolean checkName(String name) {
return this.name.equals(name);
}
}
This looks like filter.
Recall from Fundies 1:
(filter even? '(1 2 3 4)) ; returns '(2 4)
(filter odd? '(1 2 3 4)) ; returns '(1 3)
We can’t pass through the functions themselves, but we can pass objects which can hold functions:
These are called function objects
interface IPaintingPredicate {
// ask a question about a given painting
boolean apply(Painting p);
}
class ByDaVinci implements IPaintingPredicate {
//is the given Painting by DaVinci?
public boolean apply(Painting p) {
return p.artist.checkName("DanVinci");
}
}
class Before1900 implements IPaintingPredicate {
//is the given Painting painted before 1900
public boolean apply(Painting p) {
return p.year < 1900;
}
}
//...
interface ILoPainting {
//...
//filters this list of painting by the given predicate
ILoPainting filter(IPaintingPredicate pred);
}
class MtLoPainting implements ILoPainting {
//...
ILoPainting filter(IPaintingPredicate pred) {
return this;
}
}
class ConsLoPainting implements ILoPainting {
//...
//...
ILoPainting filter(IPaintingPredicate pred) {
if(pred.apply(this.first)) {
return new ConsLoPainting(this.first, this.rest.filter(pred));
} else {
return this.rest.filter(pred);
}
}
}
class Examples {
this.mt.filter(new Before1900()) -> this.mt
this.list2.filter(new ByDaVinci()) -> this.list1
}
If you want to add another way to filter something, you’d just need to make a new class in the predicate interface (and create the apply method). For example:
class Over50 implements IPaintingPredicate {
//is the given painting values at more than 50 million dollars?
public boolean apply(Painting p) {
return p.value > 50;
}
}
Abstractions over Multiple Arguments
Dot Product Example
Dot product problem. For example, (1, 2, 3).dotProduct(5, 6) should return 5+12+0 = 17
Remember, by doing double dynamic dispatch, you know whether or not that is a ConsLoInt or MtLoList (because it runs to correct method).
interface ILoInt {
int dotProduct(ILoInt that);
//helper for dot product
int dotProductHelp(int firstOfOriginalList, ILoInt restOfOriginalList);
}
class ConsLoInt implements ILoInt {
int first;
ILoInt rest;
ConsLoInt(int f, ILoInt r) {
this.first = f;
this.rest = r;
}
public int dotProduct(ILoInt that) {
return that.dotProductHelp(this.first, this.rest);
}
public int dotProductHelp(int firstOfOriginalList, ILoInt restOfOriginalList) {
return this.first * firstOfOriginalList + this.rest.dotProduct(restOfOriginalList);
}
}
class MtLoInt implements ILoInt {
public int dotProduct(ILoInt that) {
return 0;
}
public int dotProductHelp(int firstOfOriginalList, ILoInt restOfOriginalList) {
return 0;
}
}
class Examples {
ILoInt mt = new MtLoInt();
ILoInt list1 = new ConsLoInt(4, new ConsLoInt(5, this.mt));
ILoInt list2 = new ConsLoInt(1, new ConsLoInt(2, new ConsLoInt(3, this.mt)));
boolean testDot(Tester t) {
return t.checkExpect(list1.dotProduct(list1), 16+25)
&& t.checkExpect(this.list1.dotProduct(this.list2), 4+10);
}
}
List Abstractions
Filter: [X -> Boolean] [List-of X] -> [List-of X]
Map: [X -> Y] [List-of X] -> [List-of Y]
Foldr: [X Y -> Y] Y [List-of X] -> Y
Andmap: [X -> Boolean] [List-of X] -> Boolean
Ormap: [X -> Boolean] [List-of X] -> Boolean
We can’t make Foldr or Map yet because of the signature. They both return something with a Y which we don’t know.
Filter - Painting Example
Recall filter from last lecture. We use function objects to make use of overriding.
// In ConsLoPainting
public ILoPainting filter(IPaintingPredicate pred) {
if(pred.apply(this)) {
return new ConsLoPainting(this.first, this.rest.filter(pred));
} else {
return this.rest.filter(pred);
}
}
//In IPaintingPredicate
class BySomeArtist implements IPaintingPredicate {
String artistName;
BySomeArtist(String artistName) {
this.artistName = artistName;
}
// Is the given painting painted by this.artistName?
public boolean apply(Painting p) {
return p.checkArtistName(this.artistName);
}
}
class BeforeSomeYear implements IPaintingPredicate {
int year;
BeforeSomeYear(int year) {
this.year = year;
}
public boolean apply(Painting p) {
return p.year < this.year;
}
}
// Example
this.list3.filter(new BySomeArtist("Monet")) //return empty list
Ormap
//in ILoPainting
boolean ormap(IPaintingPredicate pred);
//in mt class
boolean ormap(IPaintingPredicate pred) {
return false;
}
// in cons class
boolean ormap(IPaintingPredicate pred) {
return pred.apply(this.first) || this.rest.ormap(pred);
}
Andmap
//in ILoPainting
boolean ormap(IPaintingPredicate pred);
//in mt class
boolean ormap(IPaintingPredicate pred) {
return true;
}
// in cons class
boolean ormap(IPaintingPredicate pred) {
return pred.apply(this.first) && this.rest.ormap(pred);
}
Higher Order Predicates
A predicate that takes in another predicate
(Higher order in general–like foldr–means takes in another function )
//in predicate
class AndPredicate implements IPaintingPredicate {
IPaintingPredicate left;
IPaintingPredicate right;
AndPredicate(IPaintingPredicate left, IPaintingPredicate right) {
this.left = left;
this.right = right;
}
/*
* FIELDS:
* this.left ... IPaintingPredicate
* this.right ... IPaintingPredicate
* METHODS:
* this.apply(Painting) ... Boolean
* METHODS FOR FIELDS:
* this.left.apply(Painting) ... Boolean
* this.right.apply(Painting) ... Boolean
*/
//does the painting pass both predicates?
public boolean apply(Painting p) {
return this.left.apply(p) && this.right.apply(p);
}
}
// in examples:
this.list3.filter(AndPredicate(new BySomeArtist("Monet"), new BeforeSomeYear(1900)));
You can nest these as well because it is a IPaintingPredicate. You can also do the same thing with or. Note, we can use these predicates for sorting as well.
Abstracting Over More Than One Argument
Example of sorting by year (which looks very similar to sort by title):
// In ILoPainting
// sort this list by year
ILoPainting sortByYear();
//insert the given painting into this sorted list (sorted by year)
ILoPainting insertByYear(Painting p);
// In MtLoPainting
public ILoPainting sortByYear() {
return this;
}
public ILoPainting insertByYear(Painting p) {
return new ConsLoPainting(p, this);
}
// In MtLoPainting
public ILoPainting sortByYear() {
return this.rest.sortByYear().insertByYear(this.year);
}
public ILoPainting insertByYear(Painting p) {
if (this.first.yearComesBefore(p)) {
return new ConsLoPainting(this.first, this.rest.insertByYear(p));
} else {
return new ConsLoPainting(p, this);
}
}
So we can abstract this using a comparator object:
NOTE: This isn’t the same as a predicate object because they signatures are different. The predicate’s signature is Painting -> Boolean and the comparator’s signature is Painting Painting -> Boolean (it takes in another Painting).
You do, however, have to delegate the actual comparison to the painting class
interface IPaintingComparator {
// does p1 come before p2?
boolean compare(Painting p1, Painting p2);
}
class CompareByYear implements IPaintingComparator {
// was p1 painted before p2?
boolean compare(Painting p1, Painting p2){
return p1.paintedBefore(p2);
}
}
class CompareByArtistName implements IPaintingComparator {
// does p1's artist name come before p2's artist name alphabetically
boolean compare(Painting p1, Painting p2){
return p1.nameComesBefore(p2);
}
}
We also create this compare method in our Painting class.
// in Painting class
boolean paintedBefore(Painting p) {
return this.year < p.year;
}
And the abstracted sort method looks like:
// In ILoPainting
//sort this list of painting by the given comparison operator
ILoPainting sortBy(IPaintingComparator comp);
// inserts into the sorted list
ILoPainting insertBy(IPaintingComparator comp, Painting p);
// In MtLoPainting class
//sort this list of painting by the given comparison operator
ILoPainting sortBy(IPaintingComparator comp) {
return this;
}
// inserts into the sorted list
ILoPainting insertBy(IPaintingComparator comp, Painting p) {
return new ConsLoPainting(p, this);
}
// In ConsLoPainting class
//sort this list of painting by the given comparison operator
ILoPainting sortBy(IPaintingComparator comp) {
return this.rest.sortBy(comp).insertBy(comp, this.first);
}
// inserts into the sorted list
ILoPainting insertBy(IPaintingComparator comp, Painting p) {
if (comp.compare(this.first, p)) {
return new ConsLoPainting(this.first, this.rest.insertBy(comp, p));
} else {
return new ConsLoPainting(p, this);
}
}
What if we want it to be a three value comparator (is this before that, after that, or the same as that)?
- Returns a negative int if it comes before
- Zero if it’s equal
- Positive if it comes after
// in PaintingComparator
// returns a negative int if p1 comes before p2,
// a positive int if p1 comes after p2,
// or zero if p1 is the same as p2
int compare(Painting p1, Painting p2);
// in Painting
int paintedBefore(Painting p) {
return this.year - p.year;
}
int nameComesBefore(Artist that) {
return this.name.compareTo(that.name);
}
// in ConsLoPainting
public ILoPainting insertBy(IPaintingComparator comp, Painting p) {
if (comp.compare(this.first, p) < 0) {
return new ConsLoPainting(this.first, this.rest.insertBy(comp, p));
} else {
return new ConsLoPainting(p, this);
}
}
Example - Gets the Min Painting in an List
Getting the most expensive/least expensive/earliest painted Painting
// in IPainting
// Gets the min painting based on the given comparator
Painting findMin(IPaintingComparator comp);
// Gets the min painting
// Accumulator: keeps track of the min painting so far
Painting findMinAcc(IPaintingComparator comp, Painting acc);
// in MtLoPainting
// Gets the min painting based on the given comparator
public Painting findMin(IPaintingComparator comp) {
throw new RunTimeException("No min painting in empty list");
}
// Gets the min painting
// Accumulator: keeps track of the min painting so far
Painting findMinAcc(IPaintingComparator comp, Painting acc) {
return acc;
}
// in ConsLoPainting
// Gets the min painting based on the given comparator
public Painting findMin(IPaintingComparator comp) {
return this.rest.findMinAcc(comp, this.first);
}
// Gets the min painting
// Accumulator: keeps track of the min painting so far
Painting findMinAcc(IPaintingComparator comp, Painting acc) {
if (comp.compare(this.first, acc) < 0) {
return this.rest.findMinAcc(comp, this.first);
} else {
return this.rest.findMinAcc(comp, acc);
}
}
Higher Order Comparator
A comparator that takes in another comparator
class ReverseComparator implements IPaintingComparator {
IPaintingComparator comp;
ReverseComparator(IPaintingComparator comp) {
this.comp = comp;
}
// does p2 come before p2 according to the reverse of this.comp?
public int compare(Painting p1, Painting p2) {
return this.comp.compare(p1, p2) * -1;
}
}
Abstracting Over Types
IPaintingPredicate
boolean apply(Painting P)
IBookPredicate
boolean apply(Book P)
These are similar. Can we abstract away these differences (only difference is what they take in)?
We can take in a generic type
interface IPred<T> {
boolean apply(T t);
}
Example:
class ByArtist implements IPred<Painting> {
String name;
ByArtist(String name) {
this.name = name;
}
// is the given painting painted by this.name?
boolean apply(Painting p) {
return this.name.equals(p.name);
}
}
class ByAuthor implements IPred<Book> {
String name;
ByAuthor(String name) {
this.name = name;
}
// is the given painting painted by this.name?
boolean apply(Book b) {
return this.name.equals(b.name);
}
}
Generic List
We can have one IList interface which can be a list of whatever you want. The downsides to this is that you can’t have specific methods (such as totalSumOfBooks). Cannot refer to anything specific about T. But this is where List Abstractions are helpful.
Filter: [x-> Boolean] [List-of X] -> [List-of X]
Map: [X->Y] [List-of X] -> [List-of Y]
Fold: [X Y -> Y] Y [List-of X] -> Y
NOTE: If we haven’t seen a type before, we need to say
interface IList<T> {
//filters this list by the given predicate
IList<T> filter(IPred<T> pred);
//map a function onto the members of this list
<U> IList<U> map(IFunc<T, U> f);
// combine the items in this list according to the given function
// foldr
<U> U fold(IFunc2<T, U, U> f, U base);
}
class MtList<T> implements IList<T> {
//filters this list by the given predicate
IList<T> filter(IPred<T> pred){
return this;
}
//map a function onto the members of this list
public <U> IList<U> map(IFunc<T, U> f) {
return new MtList<U>();
}
// combine the items in this list according to the given function
public <U> U fold(IFunc2<T, U, U> f, U base) {
return base;
}
}
class ConsList<T> implements IList<T> {
T first;
IList<T> rest;
ConsList(T first, IList<T> rest) {
this.first = first;
this.rest = rest;
}
//filters this list by the given predicate
IList<T> filter(IPred<T> pred){
if (pred.apply(this.first)) {
return new ConsList<T>(this.first, this.rest.filter(pred));
} else {
return this.rest.filter(pred);
}
}
//map a function onto the members of this list
public <U> IList<U> map(IFunc<T, U> f) {
return new ConsList<U>(f.apply(this.first), this.rest.map(f));
}
// combine the items in this list according to the given function
public <U> U fold(IFunc2<T, U, U> f, U base) {
return f.apply(this.first, this.rest.fold(f, base));
}
}
interface IPred<X> {
//asks a question about the given x
boolean apply(X x);
}
class ByAuthor implements IPred<Painting> {
String name;
ByAuthor(String name) {
this.name = name;
}
public boolean apply(Painting x) {
return x.checkArtistName(this.name);
}
}
interface IFunc<X, Y> {
//apply an operation to x and produce a y
Y apply(X x);
}
interface IFunc2<X, Y, Z> {
//apply some operation to x and y to produce a Z
Z apply(X x, Y y);
}
class SumValues implements IFunc2<Painting, Double, Double> {
public Double apply(Painting x, Integer y) {
return p.value + y;
}
}
class PaintingToArtist implements IFunc<Painting, Artist> {
// gets the artist of a given painting
public Artist apply(Painting x) {
return x.artist;
}
}
class Examples {
...
Painting waterlilies = new Painting(this.monet, "Water Lilies", 20, 1915);
IList<Painting> paintings = new ConsList<Painting>(this.waterlilies, new MtList<Painting>);
boolean testFilter(Tester t) {
return t.checkExpect(this.paintings.filter(new ByAuthor("Monet")), this.paintings);
}
boolean testMap(Tester t) {
return t.checkExpect(this.paintings.map(new PaintingToArtist()),
new ConsList<Artist>(this.monet, new MtList<Artist>))
&& t.checkExpect(new MtList<Painting>().map(new PaintingToArtist()),
new MtList<Artist>());
}
}
Java’s Own Implementation
Import utils for Java
java.util.function Predicate
- Instead of
apply, it has the methodtest
Function
applymethod
BiFunction
- The same as
Func2 applymethod
java.util.
Comparator
comparemethod
See official Java documentation for more information.
Visitors
Recall Generic Lists from last lecture
NOTE: You can implement multiple interfaces in a single class
...
interface IShape {
// produces a Double when this IShape is apply to by the given function
<R> R accept(IShapeVisitor<R> f);
}
class Circle implements IShape {
int x, y, radius;
String color;
Circle(int x, int y, int radius, String color) {
this.x = x;
this.y = y;
this.radius = radius;
this.color = color;
}
// produces a Double when this Circle is apply to by the given function
public <R> R accept(IShapeVisitor<R> f){
return f.visitCircle(this);
}
}
class Rect implements IShape {
int x, y, w, h;
String color;
Rect(int x, int y, int w, int h, String c) {
this.x = x;
this.y = y;
this.w = w;
this.h = h;
this.color = c;
}
// produces a Double when this Rect is apply to by the given function
public <R> R accept(IShapeVisitor<R> f){
return [f visitRect](f.visitRect)(this);
}
}
// We can say this `extends IFunc<IShape, R>` if we want every
// IShapeVisitor to be an IFunc
interface IShapeVisitor<R> {
R visitCircle(Circle c);
R visitRect(Rect r);
}
// a function to compute the area of an IShape
class ShapeArea implements IShapeVisitor<Double>{
// compute the area of a Circle
public Double visitCircle(Circle c) {
return Math.PI * c.radius * c.radius;
}
// compute the area of a Rect
public Double visitRect(Rect c) {
return r.h * r.w * 1.0;
}
// apply a function to the given shape
public Double apply(IShape x) {
return x.accept(this);
}
}
// NOTE: We could also just have every IShapeVisitor is an IFunc
class ShapeGrow implements IShapeVisitor<Shape>, IFunc<IShape, Double> {
int increment;
ShapeGrow(int i) {
this.increment = i;
}
public IShape visitCircle(Circle c) {
return new Circle(c.x, c.y, c.radius + this.increment, c.color);
}
public IShape visitRect(Rect r) {
return new Rect(r.x, r.y, r.w, r.h, r.color);
}
// apply a function to the given shape
public Double apply(IShape x) {
return x.accept(this);
}
}
class Examples {
IShape c1 = new Circle(3, 4, 10, "red");
IShape r1 = new Rectangle(6, 8, 3, 2, "blue");
IList<IShape> shapes = new ConsList<IShape>(this.c1, new ConsList<IShape>(this.r1, new MtList<IShape>()));
boolean testShapeAreas(Tester t){
return t.checkExpect(this.shapes.map(new shapeArea()),
new ConsList<Double>(Math.PI * 100, new ConsList<Double>(6.0, new MtList<Double>())));
}
}
What about the visitors for ILists?
import java.util.Function;
interface IList<T> {
<R> R accept(IListVisitor<T, R> ilv);
}
class MtList<T> implements IList<T> {
public <R> R accept(IListVisitor<T, R> ilv) {
return ilv.visitMt(this);
}
}
class ConsList<T> implements IList<T> {
T first;
IList<T> rest;
ConsList(T first, IList<T> rest) {
this.first = first;
this.rest = rest;
}
public <R> R accept(IListVisitor<T, R> ilv) {
return ilv.visitCons(this);
}
}
interface IListVisitor<T, R> {
R visitMt(MtList<T> mt);
R visitCons(ConsList<T> cons);
}
class FilterVisitor<T> implements IListVisitor<T, IList<T>> {
Predicate<T> pred;
FilterVisitor(Predicate<T> pred) {
this.pred = pred;
}
public IList<T> visitMt(MtList<T> mt) {
return mt;
}
// asks a question about the first item in the cons, recurs on the rest
public IList<T> visitCons(ConsList<T> cons) {
if (this.pred.test(cons.first)) {
return new ConsList<T>(cons.first, cons.rest.accept(this));
} else {
return this.rest.accept(this);
}
}
}
class ContainsA implements Predicate<String> {
// does the string contain the letter a?
public boolean test(String x) {
return x.contains("a") || x.contains("A");
}
}
class Examples {
// Strings2 = ["dog", "cat"]
// Strings1 = ["cat"]
boolean testFilter(Tester t) {
return t.checkExpect(this.strings2.accept(new FilterVisitor<String>(new ContainsA())), this.strings1);
}
}
Mutation
Consider:
This doesn’t work because this is circular data. How can we make an example of this?
What we want is:
t.checkExpect(this.monet.painting.artist, this.monet);
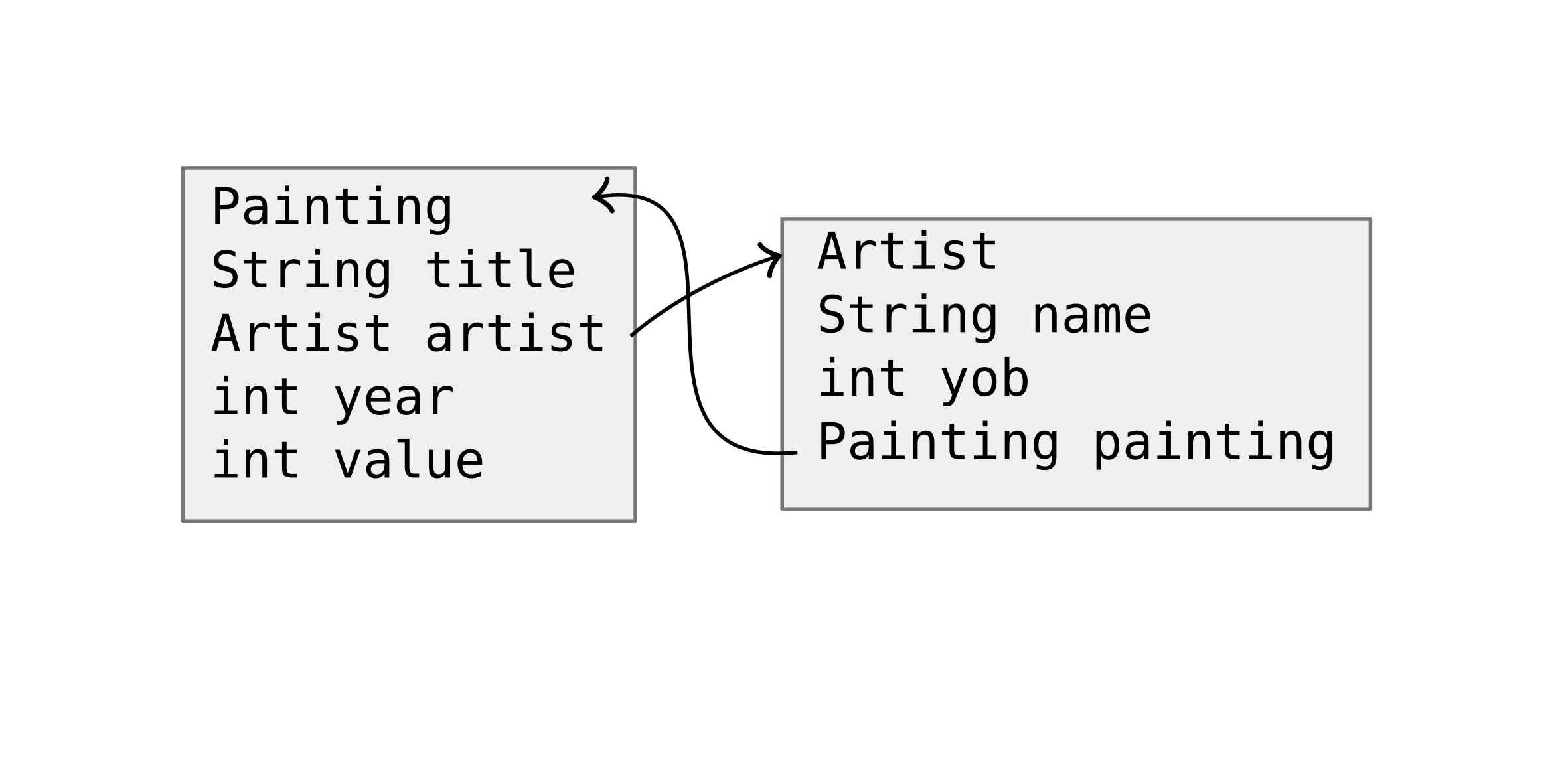
class Artist {
String name;
int yob;
Painting painting;
Artist(String n, int yob, Painting p) {
this.name = n;
this.yob = yob;
this.painting = p;
}
}
class Painting {
String title;
Artist artist;
int year;
int value;
Painting(String t, Artist a, int y, int v) {
this.title = t;
this.artist = a;
this.year = y;
this.value = v;
}
}
In order to do this, we need to start with incomplete objects:
this.monet = new Artist("Claude Monet", 1840, null);
this.waterlilies = new Painting(this.monet, "Waterlilies", 30, 1915);
// Assignment statement
this.monet.painting = this.waterlilies;
This represents:
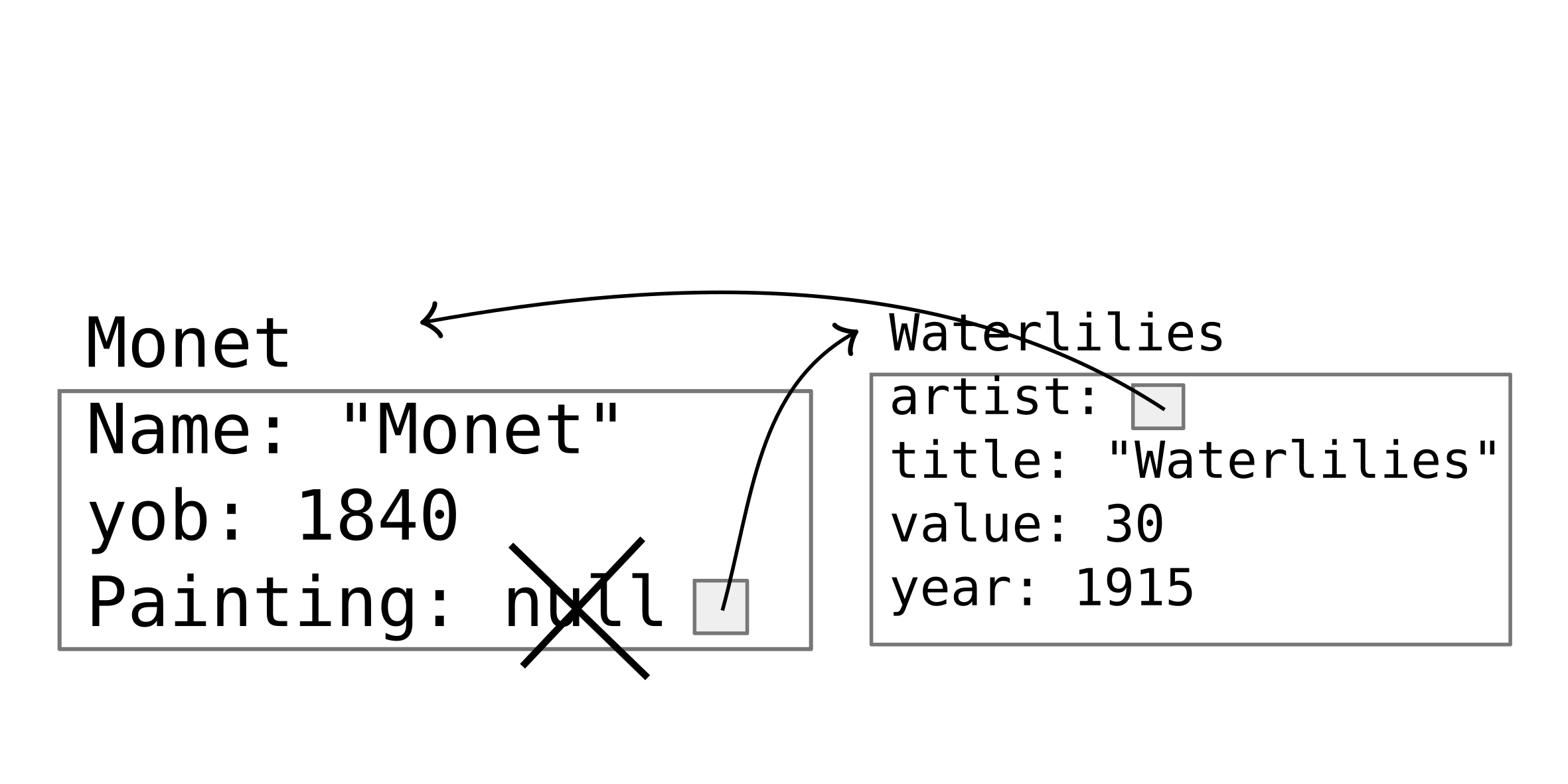
The side effect is that The Artists painting value is changed from null to waterlilies.
Now what about checking for sameness? Because we introduced circularity in our data, we have to make sure that our methods terminate.
// In Painting class
boolean samePainting(Painting p) {
return this.artist.sameArtist(p.artist)
&& this.title.equals(p.title)
&& this.value == p.value
&& this.year == p.year;
}
// In Artist class
boolean sameArtist(Artist other) {
return this.name.equals(other.name)
&& this.yob == other.yob;
// We don't include the next line because it introduces circularity
//&& this.painting.samePainting(other.painting);
}
Another example (to show how complicated this can get):
class Counter {
int val;
Counter() {
this(0);
}
Counter(int initialVal) {
this.val = initialVal;
}
int get() {
int ans = this.val;
this.val = this.val + 1;
return ans;
}
}
class ExamplesCounter {
boolean testCounter(Tester t) {
Counter c1 = new Counter();
Counter c2 = new Counter(2);
// What should these tests be?
return t.checkExpect(c1.get(), 0)// Test 1
&& t.checkExpect(c2.get(), 2)// Test 2
&& t.checkExpect(c1.get() == c1.get(), false)// Test 3
&& t.checkExpect(c2.get() == c1.get(), true)// Test 4
&& t.checkExpect(c2.get() == c1.get(), true) // Test 5
&& t.checkExpect(c1.get() == c1.get(), false) // Test 6
&& t.checkExpect(c2.get() == c1.get(), false)// Test 7
}
}
NOTE: If we pass through primitive types, it makes a copy of the value whereas if we pass in objects, it copies the reference (we will go over this in future lectures).
Another example for Painting.
Painting poppies = new Painting(this.monet, "Poppies", 20, 1873);
boolean testPainting(Tester t) {
this.monet.painting = this.poppies;
return t.checkExpect(monet.painting.artist, this.monet);
}
We want to make this more clear:
NOTE: A void method does not return anything. If a method has a side effect to running it, you have to declare an effect statement. If it also returns something, you add a purpose statement.
// In Artist class
// EFFECT: Update this Artist's painting with the given painting
void updatePainting(Painting p) {
if (this.painting != null) {
throw new RuntimeException("Artist cannot have a second painting");
} else if (!p.artist.sameArtist(this)) {
throw new RuntimeException("not the right painting for this artist");
}
} else {
this.painting = p;
}
}
// In Examples class
this.monet.updatePainting(this.waterlilies);
this.monet.updatePainting(this.poppies);
Mutation Inside Structures
Test Fixture
How to test updatePainting:
- Ensure the state of our initial conditions
- Modify the state by running the code
- Test that the changes occurred
Example:
// In Examples class
Artist monet;
Painting waterlilies;
Painting poppies;
//initialize the data to its initial conditions
void initData() {
this.monet = new Artist("Claude Monet", 1840, null);
this.waterlilies = new Painting(this.monet, "Waterlilies", 30, 1915);
this.poppies = new Painting(this.monet, "Poppies", 20, 1873);
}
boolean testPainting1(Tester t) {
//1. Ensure our initial conditions
this.initData();
//2. Run the code
this.monet.updatePainting(this.waterlilies);
//3. Test that the changes occurred
return t.checkExpect(this.monet.painting.artist, monet);
}
NOTE: Test methods are run in a random order each time.
We do not require testing initData.
NOTE: We don’t have to have our test methods return a boolean, they can return a void.
void testPainting(Tester t) {
//1. Ensure our initial conditions
this.initData()
// Check
t.checkExpect(this.monet.painitng, null);
//2. Run the code
this.monet.updatePainting(this.waterlilies);
//3. Test that the changes occurred
t.checkExpect(this.monet.painting, this.waterlilies);
}
void testPaintingsArtists(Tester t) {
this.initData();
Artist daVinci = new Artist("Leonardo da Vinci", 1452, null);
Painting mona = new Painting(this.daVinci, "Mona Lisa", 100, 1500);
t.checkExpect(this.monet.painting, null);
t.checkExpect(this.daVinci.painting, null);
t.checkException(new RuntimeException("not the right painting for this artist"),
daVinci, "updatePainting", waterlilies);
}
This linking should happen automatically:
// in Painting class
Painting(Artist artist, String title, double value, int year) {
this.artist = artist;
this.title = title;
this.value = value;
this.year = year;
this.artist.updatePainting(this);
}
// in Artist class
Artist(String name, int yob) {
this.name = name;
this.yob = yob;
}
// in Examples
Artist monet = new Artist("Monet", 1850); // Don't need to initialize the painting here
Lets make an Artist have multiple paintings.
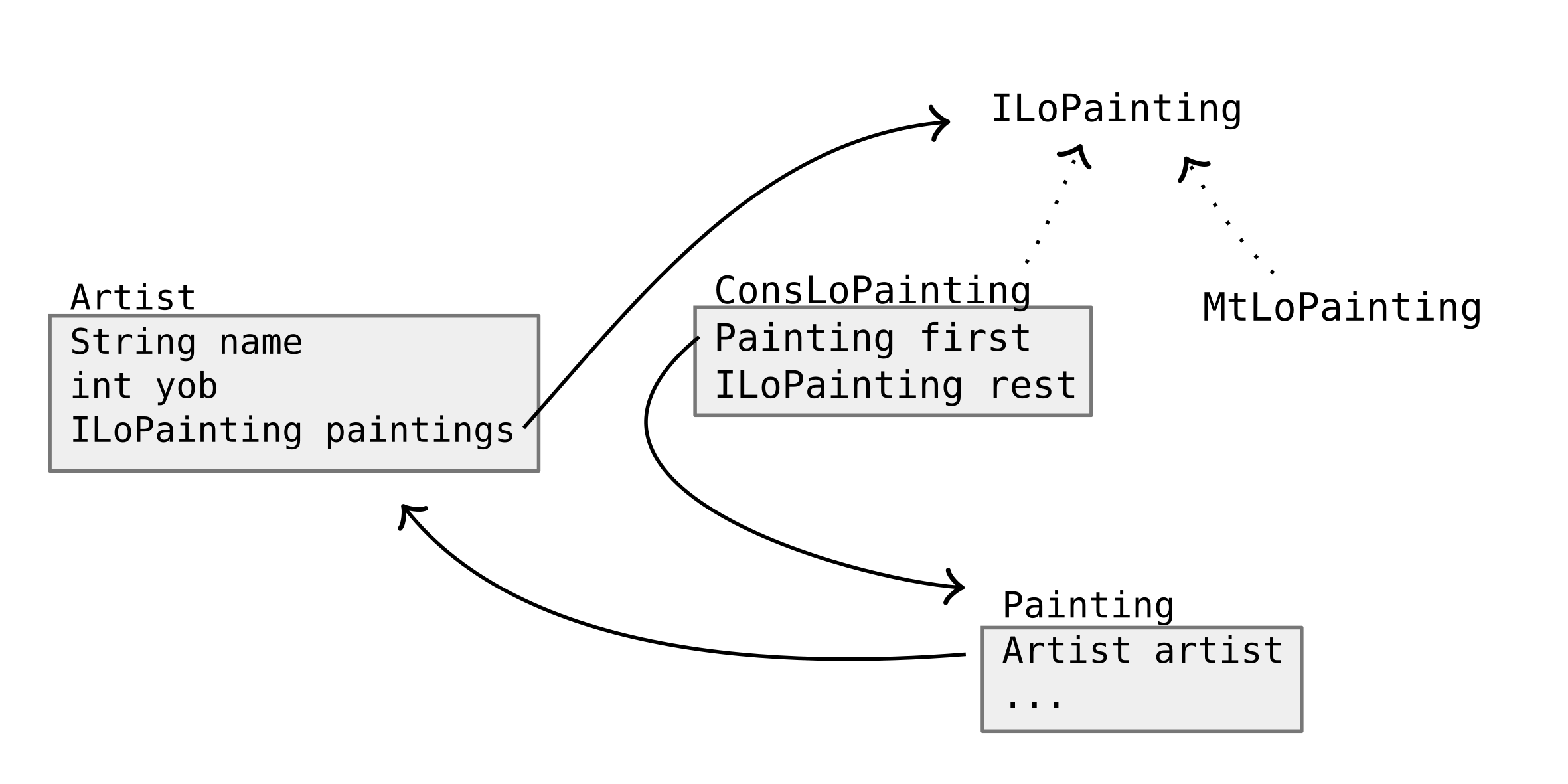
This is still circular.
// in Artist class
IList<Painting> paintings;
void updatePaintings(Painting p) {
if (!p.artist.sameArtist(this)) {
throw new RuntimeException("Artist cannot have a second painting");
} else {
this.paintings = new ConsList<Painting>(p, this.paintings);
}
}
Lambdas
You need an interface with only one method. (The input for map is that interface.)
Example:
this.strings2.map(x -> x.length());
Map takes in an IFunc and IFunc only has one method (apply).
You can also have multiple inputs:
this.strings2.map((x, y) -> x.length());
(This won’t work with our current implementation of IFunc2, but it would work if it was implemented correctly.)
Mutation, Aliasing, and Testing
When changing a person, we want to change the person object instead of creating a new object with the changed value in a list. That way, when we refer to the person in another list (or just directly), we will see the changed values.
class Person {
String name;
int phone;
Person(String name, int phone) {
this.name = name;
this.phone = phone;
}
// Returns true when the given person has the same name and phone number as this person
boolean samePerson(Person that) {
return this.name.equals(that.name) && this.phone == that.phone;
}
// Returns true when this person has the same name as a given String
boolean sameName(String name) {
return this.name.equals(name);
}
// Returns the number of this person when they have the same name as a given String
int phoneOf(String name) {
if (this.name.equals(name)) {
return this.phone;
}
else {
throw new RuntimeException("The given name does not match this person's name");
}
}
//EFFECT: changes this persons phone number to the given one
void changePhone(int newNum) {
this.phone = newNum;
}
}
interface ILoPerson {
// Returns true if this list contains a person with the given name
boolean contains(String name);
// gets the number of the person with the given name
int findPhoneNum(String name);
//EFFECT: change the number of the person with the given name
void changeNum(String name, int newNum);
}
class MtLoPerson implements ILoPerson {
public boolean contains(String name) {
return false;
}
public int findPhoneNum(String name) { return -1; }
public void changeNum(String name, int newNum) {}
}
class ConsLoPerson implements ILoPerson {
// Returns true if this non-empty list contains a person with the given name
public boolean contains(String name) {
return this.first.sameName(name) || this.rest.contains(name);
}
public int findPhoneNum(String name) {
if (this.first.sameName(name)) {
return this.first.phoneOf(name);
}
else {
return this.rest.findPhoneNum(name);
}
}
public void changeNum(String name, int newNum) {
if (this.first.sameName(name)) {
this.first.changePhone(newNum);
} else {
this.rest.changeNum(name, newNum);
}
}
}
class Examples {
...
void testChangePhoneNum(Tester t) {
this.initData()
t.checkExpect(this.friends.findPhoneNum("Frank"), 7294);
t.checkExpect(this.family.findPhoneNum("Frank"), 7294);
t.checkExpect(this.frank.phone, 7294);
this.friends.changeNum("Frank", 4927);
t.checkExpect(this.friends.findPhoneNum("Frank"), 4927);
t.checkExpect(this.family.findPhoneNum("Frank"), 4927);
t.checkExpect(this.frank.phone, 4927);
}
}
Person alice1 = new Person("Alice", 67890);
Person alice2 = new Person("Alice", 67890);
Person alice3 = this.alice1; //Alias for alice1
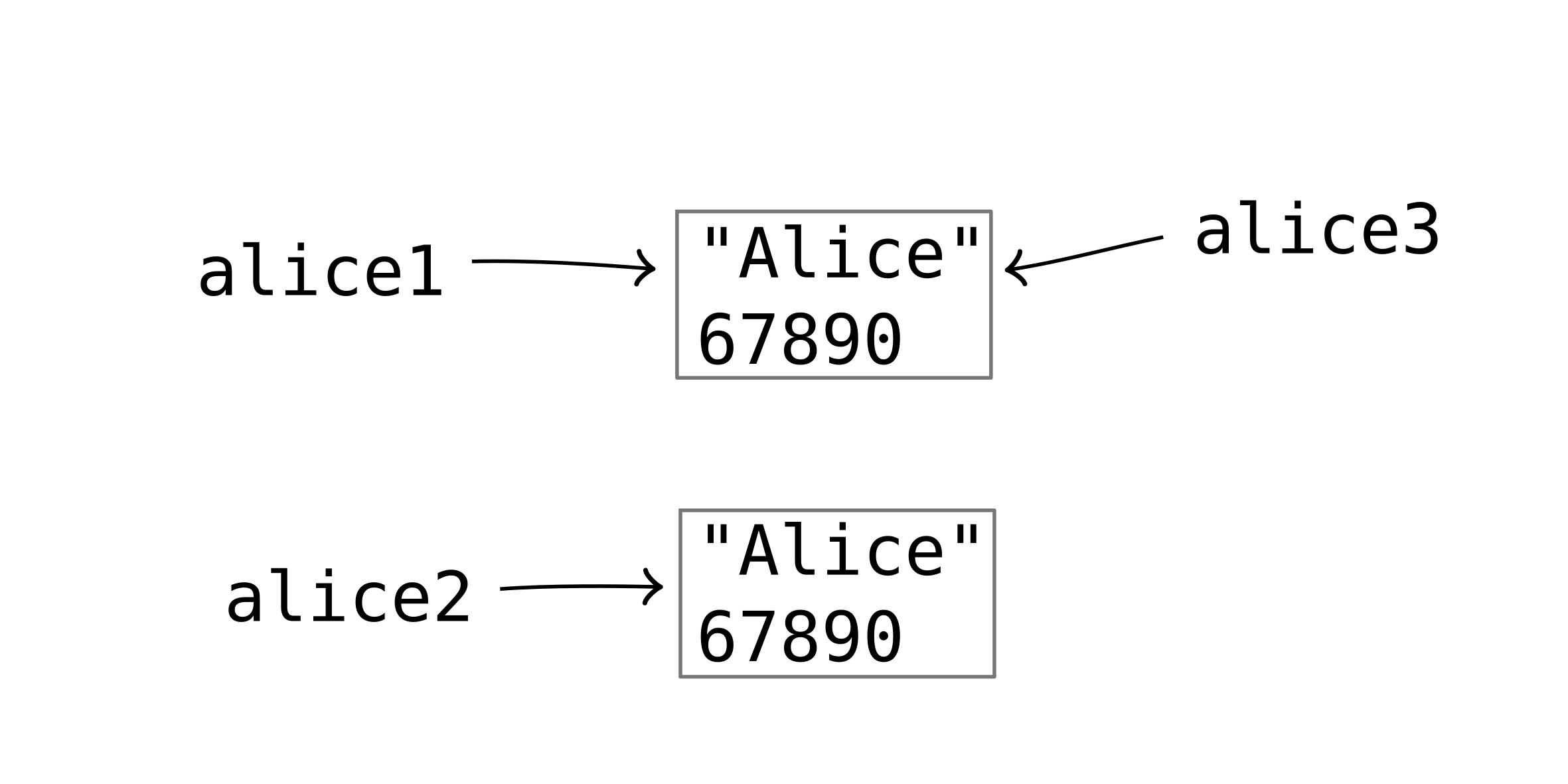
alice1.samePerson(alice2) - > true
alice1.samePerson(alice3) -> true
alice1.phone = 09676
alice1.samePerson(alice2) -> false
alice1.samePerson(alice3) -> true
Extensional Equality:
Compare objects field-by-field seeing if all the values are equivalent.
Intensional Equality:
Checks if two objects are the exact same object.
alice1.equals(alice2) -> false // Intensional equality
alice1.equals(alice3) -> true
class Counter {
int val;
Counter() {
this(0);
}
Counter(int initialVal) {
this.val = initialVal;
}
int get() {
int ans = this.val;
this.val = this.val + 1;
return ans;
}
}
class ExamplesCounter {
boolean testCounter(Tester t) {
Counter c1 = new Counter();
Counter c2 = new Counter(5);
Counter c3 = c1;
// What should these tests be?
return t.checkExpect(c1.get(), 0)// Test 1
&& t.checkExpect(c2.get(), 5)// Test 2
&& t.checkExpect(c3.get(), 1)// Test 2
&& t.checkExpect(c1.get() == c1.get(), false)// Test 3
&& t.checkExpect(c2.get() == c1.get(), true)// Test 4
&& t.checkExpect(c2.get() == c1.get(), true) // Test 5
&& t.checkExpect(c1.get() == c1.get(), false) // Test 6
&& t.checkExpect(c2.get() == c1.get(), false)// Test 7
}
}
Relating to the persons example, what if we use IList<T>
NOTE: When abstracting over types, if you want to not return anything, you use Void and in the method, you return null. (It’s an object type and not the same as void.)
interface IList<T> {
// EFFECT: modifies the first object in this list that passes the predicate
void modify(IPred<T> whichOne, IFunc<T, Void> whatToDo);
}
class MtList<T> implements IList<T> {
public T find(IPred<T> whichOne) {return null; }
// EFFECT: modifies the first object in this list that passes the predicate
void modify(IPred<T> whichOne, IFunc<T, Void> whatToDo) {}
}
class ConsList<T> implements IList<T> {
T first;
IList<T> rest;
ConsList(T first, IList<T> rest) {
this.first = first;
this.rest = rest;
}
public T find(IPred<T> whichOne) {
if (whichOne.apply(this.first)) {
return this.first;
} else {
return this.rest.find(whichOne);
}
}
// EFFECT: modifies the first object in this list that passes the predicate
void modify(IPred<T> whichOne, IFunc<T, Void> whatToDo) {
if (whichOne.apply(this.first)) {
whatToDo.apply(this.first);
} else {
this.rest.modify(whichOne, whatToDo);
}
}
}
// In the Java library, you can just use Consumer
class ChangePhone implements IFunc<Person, Void> {
int num;
ChangePhone(int num) {
this.num = num;
}
public Void apply(Person x) {
x.phone = this.num;
return null;
}
}
Mutable Data Structures
Recall the friends list from last lecture
// In ILoPerson
// EFFECT: Removes the person with the given name from this list
void removePerson(String name);
// EFFECT: Helps to remove the person with the given name
// ACCUMULATOR: Keeps track of the previous node
void removePersonHelp(String name, ConsLoPerson prev);
// In MtLoPerson
// EFFECT: Removes the person with the given name from this list
void removePerson(String name) {}
// EFFECT: Helps to remove the person with the given name
// ACCUMULATOR: Keeps track of the previous node
void removePersonHelp(String name, ConsLoPerson prev) {}
// In ConsLoPerson
// EFFECT: Removes the person with the given name from this list
void removePerson(String name) {
this.rest.removePersonHelp(name, this);
}
// EFFECT: Helps to remove the person with the given name
// ACCUMULATOR: Keeps track of the previous node
void removePersonHelp(String name, ConsLoPerson prev) {
if(this.first.sameName(name)) {
prev.rest = this.rest;
} else {
this.rest.removePersonHelp(name, this);
}
}
//in Examples
void testRemove(Tester t) {
this.initData();
t.checkExpect(this.friends.contains("Frank"), true);
t.checkExpect(this.family.contains("Frank"), true);
this.friends.removePerson("Frank");
t.checkExpect(this.friends.contains("Frank"), false);
t.checkExpect(this.family.contains("Frank"), true);
}
void testRemoveFirst(Tester t) {
this.initData();
t.checkExpect(this.friends.contains("Anne"), true);
t.checkExpect(this.family.contains("Anne"), true);
this.friends.removePerson("Anne");
t.checkExpect(this.friends.contains("Anne"), false);
t.checkExpect(this.family.contains("Anne"), true);
}
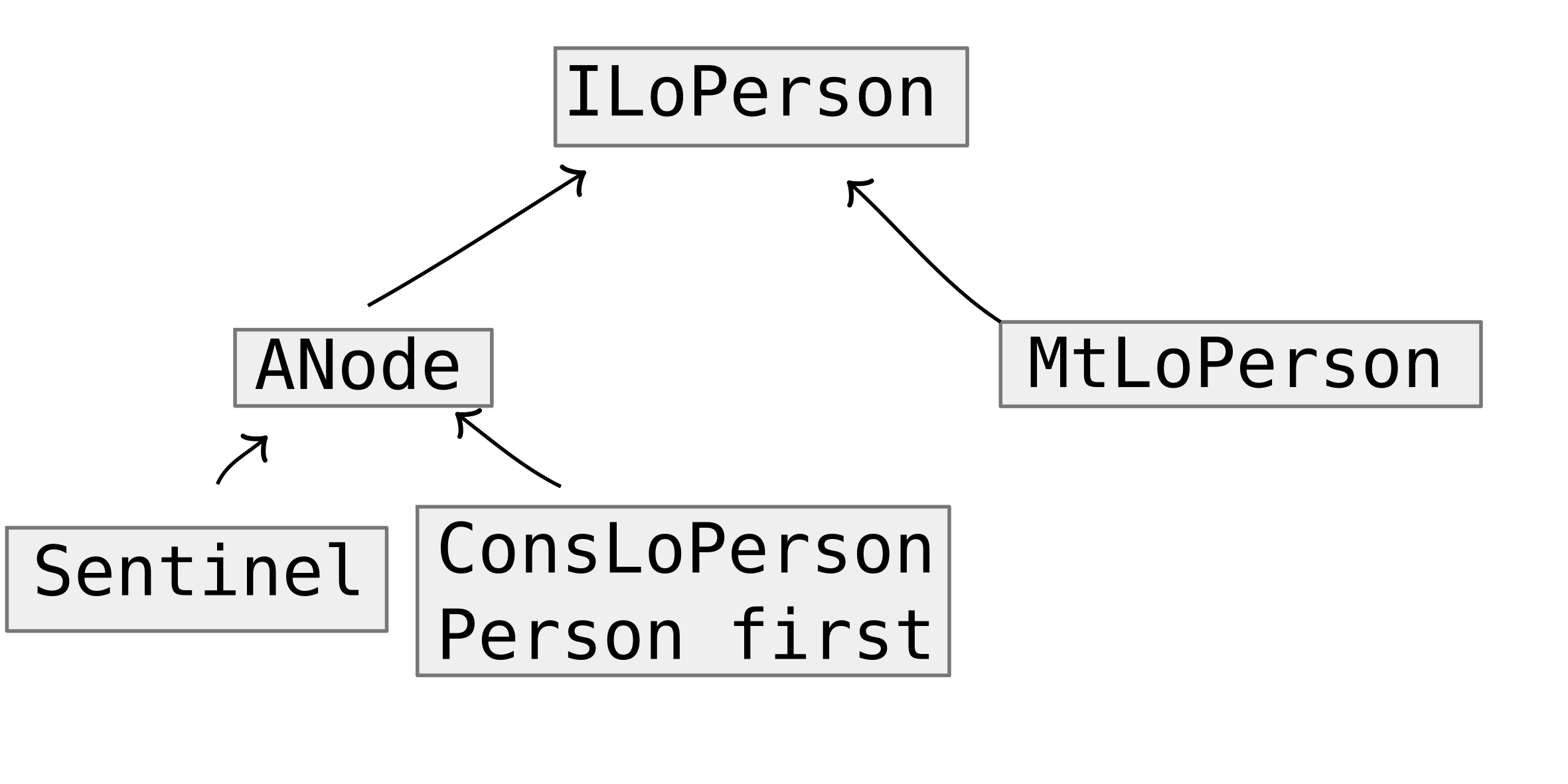
This won’t work because it can’t change the first (there is nothing before it). We need to add a sentinel which stands in front of a list and only has a rest.
Adding a layer of indirection
NOTE: Doing it this way would mean that we would always need a sentinel in front.
To make this easier, we need a wrapper:
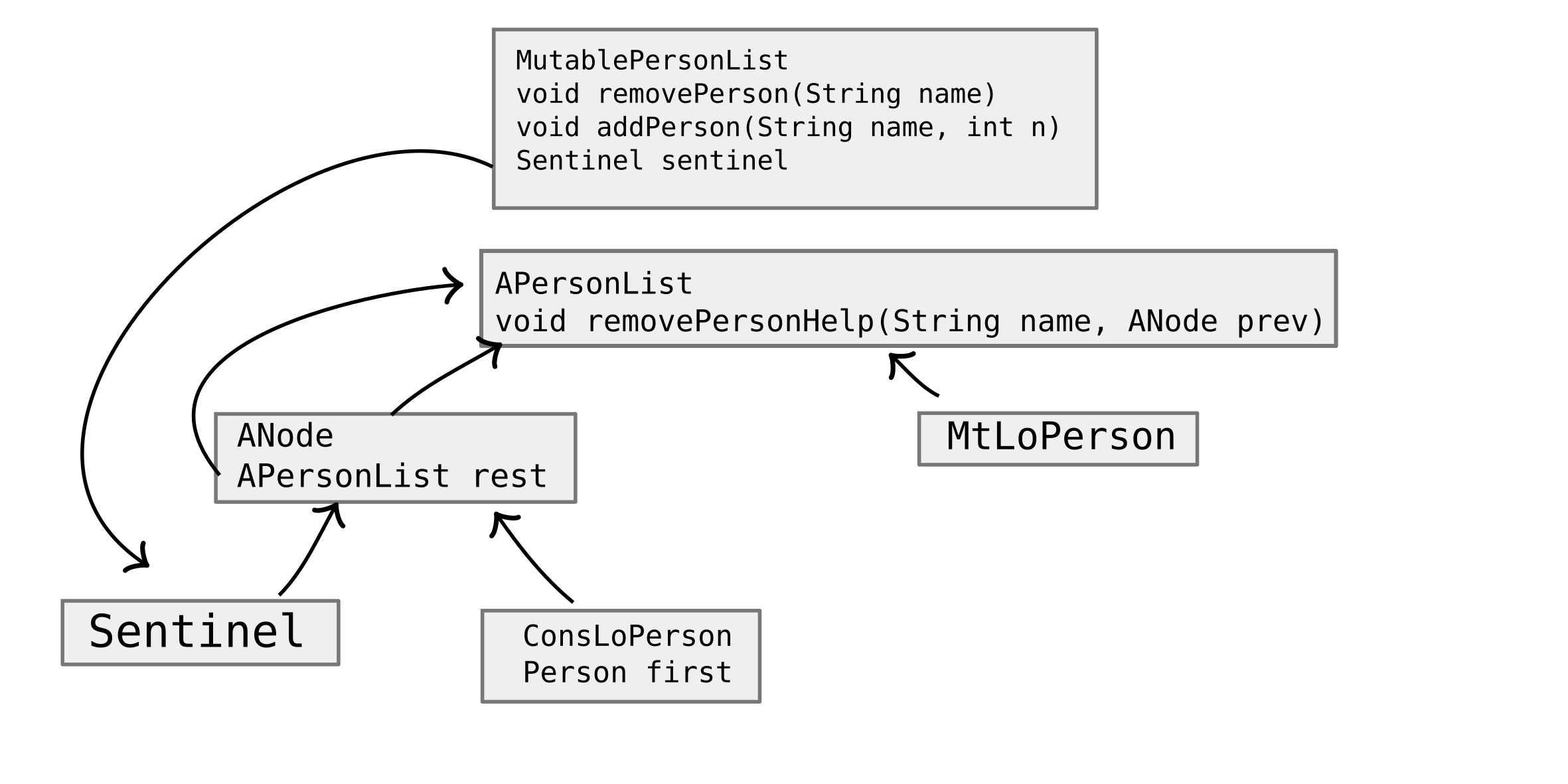
abstract class APersonList {
abstract void removePersonHelp(String name, ANode prev);
}
class MtLoPerson extends APersonList {
void removePersonHelp(String name, ANode prev) {}
}
abstract class ANode extends APersonList {
APersonList rest;
ANode(APersonList rest) {
this.rest = rest;
}
}
class ConsLoPerson extends ANode {
Person first;
ConsLoPerson(Person first, APersonList rest) {
super(rest);
this.first = first;
}
void removePersonHelp(String name, ANode prev) {
if(this.first.sameName(name)) {
prev.rest = this.rest;
} else {
this.rest.removePersonHelp(name, this);
}
}
}
class Sentinel extends ANode {
Sentinel(APerson rest) {
super(rest);
}
void removePersonHelp(String name, ANode prev) {
throw new RuntimeException("Cannot remove the sentinel");
}
}
class MutablePersonList {
Sentinel sentinel;
MutablePersonList() {
this.sentinel = new Sentinel(new MtLoPerson());
}
void removePerson(String name) {
this.sentinel.rest.removePersonHelp(name, this.sentinel);
}
}
This adds two layers of indirection.
How can we make this generic? (We will see Java’s implementation of this later)
interface IMutableList<T> {
void remove(T t); // Uses intentional equality (== or .equals)
T remove(Predicate<T> pred); // Uses extensional equality. Returns what we remove.
void addToFront(T t);
void addToEnd(T t);
void insert(T t, int n); // Adds at some index
void set(int index, T t); // Sets the element at _index_ to _t_
int size();
}
ArrayLists
Recall IMutableList from last lecture. We aren’t going to be using our own implementation, rather we are going to be using ArrayList in Java’s implementation.
ArrayLists and For Each Loops
For Each Loops
... setup ...
for (T item : list) {
... body ...
}
... use the results ...
import java.util.ArrayList;
import java.util.Arrays;
import java.util.function.Function;
import java.util.function.BiFunction;
class ArrayUtils {
// EFFECT: Swaps the items in the given list at the two given indices
<T> void swap(ArrayList<T> alist, int index1, int index2) {
// ArrayList.set returns the previous element
alist.set(index2, alist.set(index1, alist.get(index2)));
}
// map a function onto every member of the given list
<T, U> ArrayList<U> map(ArrayList<T> alist, Function<T, U> f) {
return this.mapHelp(alist, f, 0, new ArrayList<U>());
}
// map a function onto every member of the given list
<T, U> ArrayList<U> mapHelp(ArrayList<T> alist, Function<T, U> f, int current, ArrayList<U> result) {
if (alist.size() == current) {
return result;
} else {
return this.mapHelp(alist, f, current + 1, result.add(f.apply(alist.get(current))));
}
}
// map a function onto every member of the given list
<T, U> ArrayList<U> map2(ArrayList<T> alist, Function<T, U> f) {
ArrayList<U> result = new ArrayList<U>();
for (T t : alist) {
result.add(f.apply(t));
}
return result;
}
// combines the items in the given list using the given BiFunction
<T, U> U fold(ArrayList<T> alist, BiFunction<T, U, U> f, U base) {
/*
For `foldr`
ArrayList<T> reverse = new ArrayList<T>();
for (T item : alist) {
reverse.add(0, item);
}
*/
// Foldl:
U result = base;
for (T t : alist) {
result = f.apply(item, result);
}
return result;
}
// find the index of the first item that passes the given predicate
// returns -1 if the item is not found
<T> int find(ArrayList<T> alist, Predicate<T> pred) {
return this.findHelp(alist, pred, 0);
}
// find the index of the first item that passes the given predicate
// returns -1 if the item is not found
<T> int findHelp(ArrayList<T> alist, Predicate<T> pred, int current) {
if (current >= alist.size()) {
return -1;
} else if (pred.test(alist.get(current))) {
return current;
} else {
return this.findHelp(alist, pred, current+1);
}
}
}
class Examples {
ArrayList<Integer> ints;
ArrayList<String> strings;
void initData() {
this.ints = new ArrayList<Integer>();
this.ints.add(1);
this.ints.add(2);
this.ints.add(3);
this.strings = new ArrayList<String>(Arrays.asList("a", "b", "c"));
}
void testArrayLists(Tester t) {
this.initData();
t.checkExpect(this.ints.get(0), 1);
t.checkExpect(this.strings.get(2), "c");
// Will throw a IndexOutOfBounds exception
//t.checkExpect(this.strings.get(3), "c");
this.strings.add(2, "d");
t.checkExpect(this.strings.get(3), "c");
new ArrayUtils().swap(this.strings, 2, 3)
t.checkExpect(this.strings.get(3), "d");
}
void testMap(Tester t) {
this.initData();
t.checkExpect(new ArrayUtils().map(this.ints, n -> n+1),
new ArrayList<Integer>(Arrays.asList(2, 3, 4)));
}
}
Finding Something in a Sorted List
We don’t have to use find for a sorted list because that would be inefficient. Instead, we can treat it like a binary search tree. So to do that, we go to the middle and go from there.
// In ArrayListUtils
// find the index of the first String that matches target in given sorted list
// returns -1 if the item is not found
<T> int binarySearch(ArrayList<String> alist, String target) {
return this.binarySearchHelp(alist, target, 0, alist.size() -1);
}
// find the index of the first String that matches target in given sorted list
// returns -1 if the item is not found
<T> int binarySearchHelp(ArrayList<String> alist, String target, int low, int high) {
int mid = (low+high) / 2
if (low > high) {
return -1;
}
else if (target.compareTo(alist.get(mid)) == 0) {
return mid;
}
else if(target.compareTo(alist.get(mid)) > 0) {
return this.binarySearchHelp(alist, target, mid + 1, high);
}
else if(target.compareTo(alist.get(mid)) < 0) {
return this.binarySearchHelp(alist, target, low, mid - 1);
}
}
// in Examples class
ArrayList<String> strings2 = new ArrayList<String>(Arrays.asList("a", "b", "c", "d", "e", "f"));
void testFind(Tester t) {
t.checkExpect(new ArrayUtils().binarySearch(this.strings2, "b"), 1);
t.checkExpect(new ArrayUtils().binarySearch(this.strings2, "bb"), -1);
}
Sorting (Selection Sort)
Selection sort
- Find the index of the min item
- Swap with that item and the item at the front of the unsorted part
Counted For Loop
for (initialization; termination condition; update statement) {
... body ...
}
- Initialization statement: declares a loop variable, initialize to starting value, runs once
- Termination condition: checked before every iteration, if it returns false, loop terminates when this evaluates to false
- Loop body Execute at every iteration of the loop
- Update statement: executed after the loop body, used to advance the loop variable to its next value
Example:
for (int i = 0; i<10; i=i+1) {
...
}
// In ArrayListUtils
//find the index of the String that comes first alphabetically in the list
int findIndexOfMinItem(ArrayList<String> strings) {
if (strings.size() == 0) {
throw new RuntimeException("No min of an empty list");
}
int currentMin = 0;
for (int i=0; i < strings.size(); i += 1) {
if (strings.get(current).compareTo(strings.get(i)) > 0) {
currentMin = i;
}
}
return currentMin;
}
Nested For Loops
We get every combination of suits and values.
// In ArrayListUtils class
ArrayList<Card> makeDeck() {
ArrayList<Card> cards = new ArrayList<Card>();
ArrayList<String> suits = new ArrayList<String>(Arrays.asList("hearts", "diamonds", "spades", "clubs"));
ArrayList<String> values = new ArrayList<String>(Arrays.asList("ace", "two", "three", "four"));
for (int i = 0; i < values.size(); i += 1) {
for (int j = 0; j < suits.size(); j += 1) {
cards.add(new Card(values.get(i), suits.get(j)));
}
}
return cards;
}
// Outside of ArraylistUtils class
class Card {
String value;
String suit;
Card(String value, String suit) {
this.value = value;
this.suit = suit;
}
}
For-each and Counted-for Loops
Example - Build list
// In ArrayListUtil
// Build a list by applying the given function to natural numbers starting
// from 0 to n-1
<U> ArrayList<U> buildList(int num, Function<Integer, U> func) {
ArrayList<U> result = new ArrayList<U>();
for (int i = 0; i < num; i += 1) {
result.add(func.apply(i));
}
return result;
}
Consider the Cartesian points.
class CartPt {
int x;
int y;
CartPt(int x, int y) {
this.x = x;
this.y = y;
}
// EFFECT: Shifts this CartPt by a given dx and dy
void shift(int dx, int dy) {
this.x = this.x + dx;
this.y = this.y + dy;
}
// Prints this object
// Overrides the default toString which is OBJECTCLASS@numsandletters
// Works with System.out.println
public String toString() {
return "[" + this.x + ", " + this.y + "]";
}
}
Example - shiftPoints
How can we shift all of the points in a given ArrayList by a given dx, dy?
3 choices for shiftPoints:
- Try to remove the current point and then add a new shifted point
- Problematic because we are adding/removing an element while we are trying to iterating over the list
- You can get a
ConcurrentModificationException
- Change the point to be a new Cartesian point that is shifted.
- See below on why this won’t work
- Modify the current point
- This works
// In ArrayListUtils
// EFFECT: shifts all of the points in the given list by the given increments
void shiftPoints(ArrayList<CartPt> points, int x, int y) {
/*
// Option 2:
for (CartPt pt : points) {
pt = new CartPt(pt.x + x, pt.y + y);
}
*/
// Option 3:
for (CartPt pt: points) {
pt.shift(x, y);
}
}
// In Examples
ArrayList<CartPt> pointsList = new ArrayList<CartPt>(Arrays.asList(new CartPt(3, 4), new CartPt(6, 8)));
Why option 2 doesn’t work:
When we change pt, we don’t actually change anything in the list because we are only changing what pt points to.
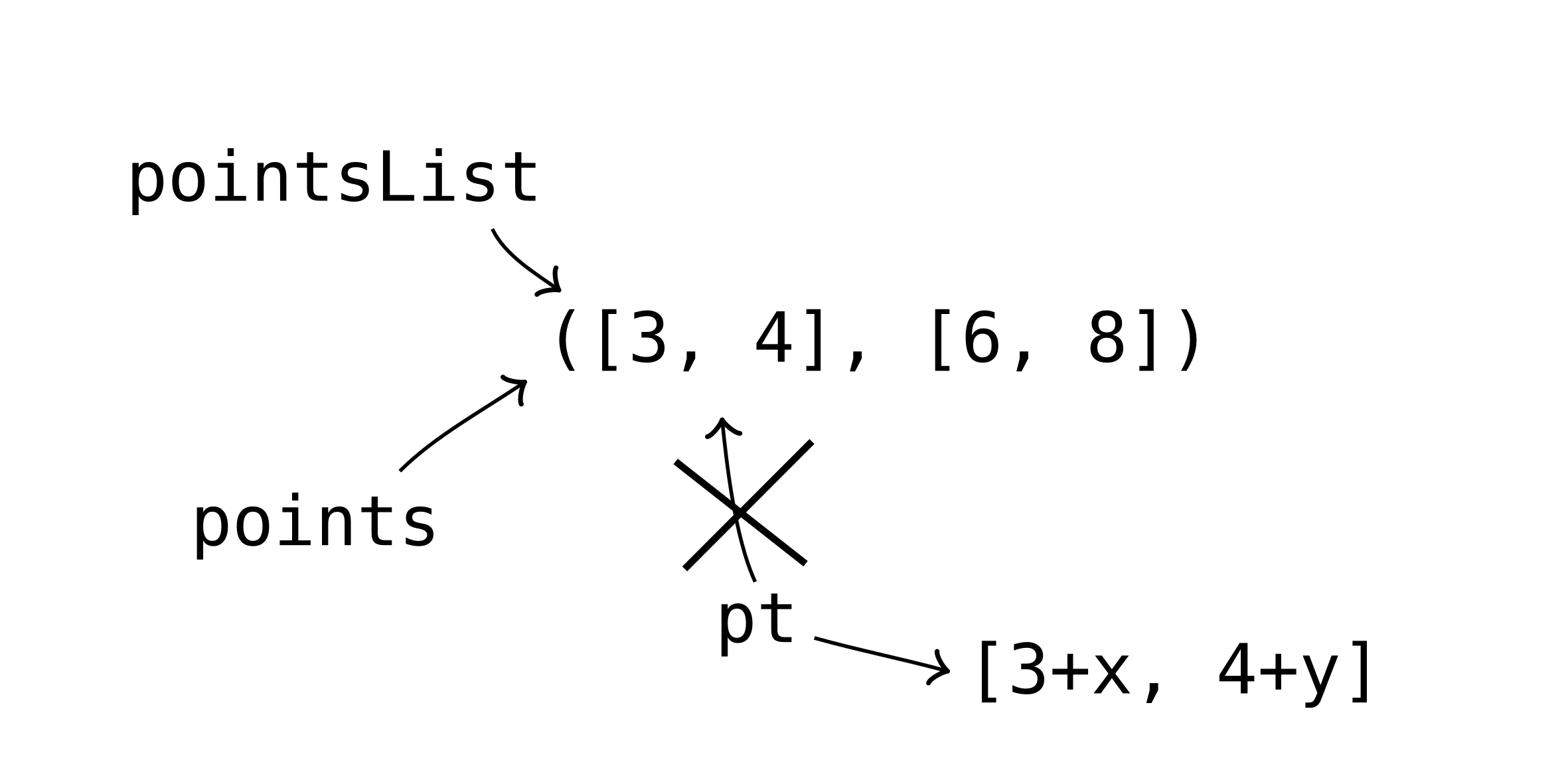
How can we shift every CartPt in a 2 dimensional array?
// in Examples
void test2dArray(Tester t) {
ArrayList<ArrayList<CartPt>> twoDArray = new ArrayList<ArrayList<CartPt>>();
ArrayList<CartPt> temp;
for (int i = 0; i < 3; i += 1) {
temp = new ArrayList<CartPt>();
for (int j = 0; j < 3; j += 1) {
temp.add(new CartPt(i, j));
}
twoDArray.add(temp);
}
// Don't test like this, but this shows a good representation
for (int i = 0; i < twoDArray.size(); i += 1) {
System.out.println(twoDArray.get(i));
}
// Shifting every CartPt in a 2D array
for (int i = 0; i < twoDArray.size(); i += 1) {
for (int j = 0; j < twoDArray.size(); i += 1) {
twoDArray.get(i).get(j).shift(0, 1);
}
}
for (int i = 0; i < twoDArray.size(); i += 1) {
System.out.println(twoDArray.get(i));
}
}
Differences in Incrementation
++i : Pre increment
- Increments
i, then assigns
i++ : Post increment
- Assigns, then increments
i
++i: (the “more correct” option)
i = i + 1return i
i++:
int j = iCached value ofii = i + 1return j
Examples:
int i = 0
int x = i++ (x=0, i=1)
int y = ++i (y=2, i=2)
Example Problem with Aliases
Example:
class Weather {
String description;
Weather(String description) {
this.description = description;
}
}
class Examples {
void F2(Weather s1) {
Weather s2 = s1;
s2.weather = "rain";
}
String question2() {
Weather sunny = new Weather("sun");
F2(sunny);
return sunny.description;
}
void testWeather(Tester t) {
// What will this return?
t.checkExpect(this.question2(), "rain");
}
}
Example 2:
class Weather {
String description;
Weather(String description) {
this.description = description;
}
}
class Hurricane {
String name;
int severity;
Weather weather;
Hurricane(String name, int severity, Weather weather) {
this.name = name;
this.severity = severity;
this.weather = weather;
}
}
class Examples {
void F3(Weather w1) {
Hurricane jane = new Hurricane("Jane", 5, w1);
jane.weather.description = "thunder";
}
String question3() {
Weather hail = Weather("hail");
Hurricane sally = new Hurricane("sally", 3, hail);
F3(hail);
return hai.description;
}
void testWeather(Tester t) {
// What will this return?
t.checkExpect(this.question3(), "thunder");
}
}
While Loops
Recall counted for loops:
for (init ; termination condition; update) {
... body ...
}
While Loops:
... initialize ...
while(termination condition) {
... body ...
... update ...
}
We use while loops when we don’t know when we want to terminate.
Example - Collatz Conjecture
(3n+1 problem)
$f(n)$
- $\frac{n}{2}$ if $n$ is even
- $3n+1$ if $n$ is odd
$f(8) \to 4 \to 2 \to 1$
$f(7) \to 22 \to 11 \to 34 \to 17$
$\to 52 \to 26 \to 13 \to 40 \to 20 \to 10 \to 5 \to 16 \to 8 \to 4 \to 2 \to 1$
// will we reach 1 using collatz conjecture?
boolean collatz(int n) { // n > 0
while (n > 1) {
if (n % 2 == 0) {
n = n/2;
}
else {
n = 3n + 1;
}
}
return true;
}
Examples - binarySearch
// In ArrayListUtils
// find the index of the first String that matches target in given sorted list
// returns -1 if the item is not found
<T> int binarySearch(ArrayList<String> alist, String target) {
int low = 0;
int high = alist.size() - 1;
while(low < high) {
int mid = (low + high) / 2;
if (alist.get(mid).compareTo(target) == 0) {
// We found it
return mid;
}
else if (alist.get(mid).compareTo(target) < 0) {
low = mid + 1;
}
else {
high = mid - 1;
}
}
return -1;
}
Loops
- for each
- counted for
- while
Every while can be a counted for and every counted for can be a for each
Use the simplest for the given problem.
Iterators and Iterable
What we want to do:
//assuming I have an ArrayList called alist
for (T t : alist) {
... do something ...
}
// in English this is what we want
while (there are more items in alist) {
T t = get next item
... do something ...
// We need to keep track of the state
}
Remember: Always call hasNext before you try to get the next!
The code:
// This is already implemented in Java. See documentation
interface Iterator<T> {
// are there any more items to process?
boolean hasNext();
// gets the next item to process
// Usually advances to the item following the one returned
T next();
}
// This is also already implemented in Java. See documentation
interface Iterable<T> {
Iterator<T> iterator();
}
// Already implemented in Java
class ArrayList<T> implements Iterable<T> {
...
Iterator<T> iterator() {
// And the ArrayListIterator implements Iterator
return new ArrayListIterator<T>(this);
}
}
class ArrayListIterator<T> implements Iterator<T> {
ArrayList<T> items;
int currentIndex;
ArrayListIterator(ArrayList<T> items) {
this.items = items;
this.currentIndex = 0;
}
// are there any more items to process?
public boolean hasNext() {
return this.currentIndex < this.items.size();
}
// gets the next item to process
// EFFECT: Add 1 to the current index
public T next() {
T result = this.items.get(this.currentIndex);
this.currentIndex++
return result;
// OR (this might work)
//return this.items.get(this.currentIndex++);
}
}
// In Examples class
Iterator<T> arrayListIter = new ArrayListIterator<T>(alist);
// What a for each loop does behind the scenes
while(arrayListIter.hasNext()) {
T t = arrayListIter.next();
... body ...
}
Example - Linked Lists
// You have to use `extends` when it's an interface
interface IList<T> extends Iterable<T> {
// Is this list a cons?
boolean isCons();
}
class MtList<T> implements IList<T> {
// returns an Iterator especially for this empty list
public Iterator<T> iterator() {
return new IListIterator<T>(this);
}
// Is this list a cons?
public boolean isCons() {
return false;
}
}
class ConsList<T> implements IList<T> {
T first;
IList<T> rest;
ConsList(T first, IList<T> rest) {
this.first = first;
this.rest = rest;
}
// returns an Iterator especially for this non-empty list
public Iterator<T> iterator() {
return IListIterator<T>(this):
}
// Is this list a cons?
public boolean isCons() {
return true;
}
}
class IListIterator<T> implements Iterator<T> {
IList<T> items;
IListIterator(IList<T> items) {
this.items = items;
}
// are there any more items to process?
public boolean hasNext() {
return this.items.isCons();
}
// gets the next item to process
// EFFECT: Queues the next
public T next() {
ConsList<T> cons = (ConsList<T>) this.items;
T answer = cons.first;
items = cons.rest;
return answer;
}
}
// We can now use for each loops with our custom ILists
class Examples {
// ints2 = [2, 1]
int result = 0;
for (Integer i : ints2) {
result += i;
}
// checkExpect(result, 3) -> true
// strings = ["cat", "dog"]
Strings = "";
for (String i : strings) {
s += i;
}
// checkExpect(Strings, "catdog") -> true
}
Examples - Unstructured Iterables
class Evens implements Iterator<Integer>, Iterable<Integer> {
int currentEven;
Evens() {
this.currentEven = 0;
}
Evens(int n) {
if (n % 2 == 0) {
this.currentEven = n;
} else {
throw new IllegalArgumentException("currentEven must be even!");
}
}
// is there another even number to produce?
public boolean hasNext() {
return true;
}
// produces the next even number
// EFFECT: currentEven is increased by 2
public Integer next() {
// NOTE: Because int is a primitive type, answer doesn't hold a
// reference to the data, it stored the data itself (an integer)
int answer = this.currentEven;
this.currentEven += 2;
return answer;
}
// Returns the iterator
public Iterator<Integer> iterator() {
return this;
}
}
NOTE: We can’t use a for each loop with this because it will never stop (see the method hasNext).
Higher-order Iterators
Let’s do the EveryOther iterator. Produces every other item from a given iterator.
class EveryOther<T> implements Iterator<T> {
Iterator<T> source;
EveryOther(Iterator<T> source) {
this.source = source;
}
/*
fields:
this.source ... Iterator
methods:
this.hasNext() ... boolean
this.next() ... T
methods for fields:
this.source.hasNext() ... boolean
this.source.next() ... T
*/
// is there another item to produce
public boolean hasNext() {
return this.source.hasNext();
}
// produce the next item
// EFFECT: source calls next a second time to skip over the item
// after the one produced
public T next() {
T temp = this.source.next;
// We need to make sure that there is yet another item
if (this.source.hasNext()) {
this.source.next();
}
return temp;
}
}
class Examples {
// strings2 = ["bird", "cat", "dog"] of type IList
EveryOther<String> eo = new EveryOther<String>(this.strings2.iterator());
EveryOther<Integer> eo2 = new EveryOther<Integer>(
new ArrayList<Integer>(Arrays.asList(1, 2 ,3)).iterator());
void testIListIterator(Tester t) {
t.checkExpect(this.eo.hasNext(), true);
t.checkExpect(this.eo.next(), "bird");
t.checkExpect(this.eo.hasNext(), true);
t.checkExpect(this.eo.next(), "dog");
t.checkExpect(this.eo.hasNext(), false);
//t.checkExpect(this.eo.next(), "dog"); // throws a ClassCastException
}
}
Examples - Trees
Breadth first traversal order: A, B, C, D, E, F, G
Depth first traversal order: A, B, D, E, C, F, G
In order traversal: D, B, E, A, F, C, G
Consider the Binary Search Tree data structure?
interface IBT<T> extends Iterable<T> {
//is this IBT a Node?
boolean isNode();
}
class BTLeaf<T> implements IBT<T> {
//is this tree a Node?
public boolean isNode() {
return false;
}
// produces an iterator for this leaf
public Iterator<T> iterator() {
return new BFIter<T>(this);
}
}
class BTNode<T> implements IBT<T> {
T data;
IBT<T> left;
IBT<T> right;
BTNode(T data, IBT<T> left, IBT<T> right) {
this.data = data;
this.left = left;
this.right = right;
}
//is this tree a Node?
public boolean isNode() {
return true;
}
// produces an iterator for this node
public Iterator<T> iterator() {
return new BFIter<T>(this);
}
}
Iterator and iterable for the tree:
(This is for both Breadth and Depth first traversals)
// Breadth first
class BFIter<T> implements Iterator<T> {
// Worklist
Deque<IBT<T>> worklist; // See assignment 8 for the code
BFIter(IBT<T> source) {
this.worklist = new Deque<IBT<T>>();
this.addIfNode(source);
}
// EFFECT: Adds the given tree to the worklist if the tree is a Node
void addIfNode(IBT<T> tree) {
if (tree.isNode()) {
this.worklist.addAtTail(tree);
}
}
// Is there another item to process?
public boolean hasNext() {
return worklist.size() > 0;
}
// Gets the next
// EFFECT: Queues up the next
public T next() {
BTNode<T> currentNode = (BTNode<T>) this.worklist.removeFromHead();
this.addIfNode(currentNode.left);
this.addIfNode(currentNode.right);
return currentNode.data;
}
}
// Depth first
class DFIter<T> implements Iterator<T> {
// Worklist
Deque<IBT<T>> worklist; // See assignment 8 for the code
DFIter(IBT<T> source) {
this.worklist = new Deque<IBT<T>>();
this.addIfNode(source);
}
// EFFECT: Adds the given tree to the worklist if the tree is a Node
void addIfNode(IBT<T> tree) {
if (tree.isNode()) {
this.worklist.addAtHead(tree); // The only difference
}
}
// Is there another item to process?
public boolean hasNext() {
return worklist.size() > 0;
}
// Gets the next
// EFFECT: Queues up the next
public T next() {
BTNode<T> currentNode = (BTNode<T>) this.worklist.removeFromHead();
this.addIfNode(currentNode.right);
this.addIfNode(currentNode.left); // Also need to switch this if you want left first
return currentNode.data;
}
}
class Examples {
void testBFIter(Tester t) {
String result = "";
// NOTE: aNode is the tree shown above
for (String s : aNode) {
result += s;
}
t.checkExpect(result, "ABCDEFG");
}
}
In BFIter: treat worklist like a queue
- First in, first out
In DFIter: treat worklist like a stack
- Last in, first out
Exam 2
Covers everything up to (and including) Lecture 26 (Hashing and Equality)
3pm to midnight
On Canvas
Lab will be review
Hashing and Equality
Consider a DictionaryEntry and WikiEntry. We want to be able to search for definitions easily.
DictionaryEntry:
- String word
- String meaning
Wiki Entry:
- String URL
- String contents
Types of structures that we’ve seen so far:
- IList
- ArrayList
- BT
- BST
- Deque
What functionality we want to add (and we want to have them efficient)
- find
- add
- delete
- modify
Right now, a sorted ArrayList or a Binary Search tree would be the most efficient.
It doesn’t make sense to store WikiEntrys in alphabetical order.
Consider people and their phone numbers:
Bob: 1234 Alice: 2345 Juan: 3456
We can make a summarizing function that gets the length of the string. For example summerizingFunction(bob) -> 3.
Therefore, we put Bob at index 3, Alice at 5, and Juan at 4. Now, searching does not depend on the size of the structure (significantly more efficient).
But what if we want to add Sally (with # 4567). She has the same name length (therefore same summarizing function result) as Alice. This is called a collision.
Collision solutions
- Linear Probing: Put it in the next available spot (but it can get messy)
- Chaining: Have each spot be another ArrayList (but we lose some of our efficiency)
- Summarizing function needs to produce more unique numbers
- Chaining + A second summarizing function
- Increase the size of our ArrayList
Java’s implementation:
Map<Key, Value> // An interface in java
HashMap<Key, Value> // A class that we will be using
HashMap’s methods
- put(Key k, Value v)
- get(Object key)
Map<Key, Value> phones = new HashMap<String, int>();
// In initData
phones.put("bob", 1234);
phones.put("alice", 2345);
phones.get("bob") -> 1234
phones.get("sally") -> null
phones.containsKey("sally") -> false
//therefore the null above means that sally
//is not there as opposed to that sally's value is null
Every Object has a hashCode method. What is it?
For Strings: “Bob”
$s(0) * 31^{length - 1} + s(1) * 31^{length-2} …$
So for “bob” it would be:
$”b” * 31 ^2 + “o” * 31 ^1 + “b” * 31^0$
2 objects may have the same HashMap
Once you went to the location, it checks to make sure that you got the right one with .equals(). Note that .equals() doesn’t always work with our custom Classes.
Consider a Book class:
Book
- String title
- int year
Author
- String name
- int yob
Book cswr = new Book("Chicken Soup with Rice", 1962);
Author ms = new Author("Maurice Sendak", 1928);
Map<Author, Book> map1 = new HashMap<Author, Book>();
// The default summary function is based off of references
map1.put(this.ms, this.cswr);
map1.get(this.ms) -> this.cswr
map1.get(new Author("Maurice Sendak", 1928)) -> null
// the above line doesn't work because it is a different object in memory
// (this is a result of the issue with .equals() )
We want to use extensional equality, not just intentional equality.
We need to override the .equals() method. This is the only place in this class that we are allowed to use instanceof and casting.
// in Author class
boolean equals(Object o) {
if (o instanceof Author) {
Author that = (Author) o;
return that.name.equals(this.name) && that.yob == this.yob;
} else {
return false;
}
}
// in Book class
boolean equals(Object o) {
if (o instanceof Book) {
Book that = (Book) o;
return that.title.equals(this.title) && this.year == that.year;
} else {
return false;
}
}
We need to also make a new summarizing function that isn’t based off of references but rather based on the data.
2 objects that evaluate to equals, must have the same hash code, so we must override has code as well as overriding .equals().
Recall that instanceof is too lenient.
Consider Posn and ColorPosn (which extends Posn)
Posn
- int x
- int y
ColorPosn
- int x
- int y
- Color color
// in Posn class
public boolean equals(Object o) {
if (o instanceof Posn) {
Posn that = (Posn) o;
return that.canEqual(o) && this.x == that.y
&& this.y == that.y;
} else {
return false;
}
}
boolean canEqual(Object o) {
return o instanceof Posn;
}
// In ColorPosn class
public boolean equals(Object o) {
if (o instanceof ColorPosn) {
ColorPosn that = (ColorPosn) o;
return that.canEqual(o) && this.x == that.x &&
this.y == that.y && this.color.equals(that.color);
} else {
return false;
}
}
// can the given be equal to this Posn?
boolean canEqual(Object o) {
return o instance of ColorPosn;
}
// in Author class
// produce a hash code for this author
int hasCode() {
return this.yob * 37 + this.name.hashCode();
}
Rule for overriding hash codes: must use a subset of the fields used in the overriding .equals() when overriding hashCode().
Now, because the hash code is dependent only on the data inside a structure, two structures with the same data will result in the same hash code.
You cannot use mutable fields when getting the hash code.
Introduction to Big-O Analysis
Introducing performance analysis
Analyze a few algorithms
What we’ve done
- Sorting
- Finding
- Inserting

Does this mean that B is better? Well we don’t have enough information
Now, we can see that A performs better with greater inputs. But now we have another issue: time. Different computers can perform tasks at different speeds, therefore we need to express running time in terms of size of the input.
What we need to consider:
- We need to count the number of operations as a function of the input.
- Since many algorithms are recursive, the performance at one size will depend on the performance at another size.
- Want to say a function’s performance is no bigger than another function or no smaller than another.
- Reflexivity, symmetry, transitivity apply to comparisons of algorithms’ performance
$T(n)$ : running time of an algorithm
$g(n)$ : running time another algorithm
$T(n) \le c * g(n)$, choose $n_0$ and $c > 0$.
For example:
$T(n) = n$
$g(n) = n^2$
Yes; $n \le c * n^2$ ($c=1$ and $n_0 = 2$)
Therefore we can say:
$T(n) \in O(g(n))$
- The big O states the upper bound – the worst case
Consider another example:
$T(n) = n^2$
$g(n) = n$
$n^2 \le c * n$
- No; as big as
cis, $n^2$ will always catch up
$T(n) \not\in O(g(n))$
To describe $T(n)$, we can use big Omega notation:
$T(n) \in \Omega (g(n))$ if $T(n) \ge c * g(x)$
- The big Omega states the lower board
$n^2 \ge c * n$
Cost Model
Cost Model (operations)
What we’ll encounter (and their cost)
- Constants - 0 units of work
- Arithmetic - 1 + cost of any sub-expressions
- Method invocation - 1 + cost of evaluating any arguments of the method + cost of evaluating the body of the method
- Statements (if, return, etc.) - 1 + cost of any sub-expressions
Cost Model (space)
- each object created - 1
Example - IList
Consider IList’s length method.
// In ConsList class
public int length() {
return 1 + this.rest.length();
}
// In MtList class
public int length() {
return 0;
}
| n | cost |
|---|---|
| 0 | 1+1 |
| >0 | 2 + this.rest.length() |
Recurrence Definition:
$T(n) = 2$ when $n=0$
$T(n) = 2 + T(n-1)$ when $n >0$
$T(n) = 2 + T(n-1)$
$2n + 2 \in O(n)$
$2n + 2 \le c * n$ therefore it is linear
$2 \le cn - 2n$
$2 \le n(c-2)$
Say, $c = 8$
$n_0 = 2$
Quicksort and Merge Sort
Insertion Sort
// In ILoInt
ILoInt nsort();
ILoInt insert(int n);
// In Mt
ILoInt nsort() {
return this;
}
ILoInt insert(int n) {
return new ConsLoInt(n, this);
}
// In Cons
ILoInt nsort() {
return this.rest.nsort().insert(this.first);
}
ILoInt insert(int n) {
if (this.first < n) {
return new ConsLoInt(this.first, this.rest.insert(n));
} else {
return new ConsLoInt(n, this);
}
}
Let’s do some Big-O analysis on this:
Insert Method
$T_{\text{insert}} (n)$:
- Best Case: $\Omega (1)$
- Worst Case: $O(n)$
$M_{\text{insert}} (n)$:
- Best Case: $\Omega (1)$
- Worst Case: $O(n)$
$1 \le T_{\text{insert}} (n) \le 3n + 1$
$1 \le M_{\text{insert}} (n) \le 3n + 1$
Best Case:
$T_{\text{best insert}} (n)$
| n | cost |
|---|---|
| 0 | 1 |
| >0 | 1 |
$M_{\text{best insert}} (n)$
| n | cost |
|---|---|
| 0 | 1 |
| >0 | 1 |
Worst Case:
$T_{\text{worst insert}} (n) = 3n + 1$
| n | cost |
|---|---|
| 0 | 1 |
| >0 | 3 + $T_{\text{worst insert}} (n-1)$ |
$M_{\text{worst insert}} (n) = n + 1$
| n | cost |
|---|---|
| 0 | 1 |
| >0 | 1 + $M_{\text{worst insert}} (n-1)$ |
Sort Method
Best Case:
$T_{\text{best sort}} (n) = T_{\text{best sort}} (n-1) + 1 = n+1$
$T_{\text{best sort}} \in \Omega (n)$
$M_{\text{best sort}} (n) = M_{\text{best sort}} (n-1) + 1 = n+1$
$M_{\text{best sort}} \in \Omega (n)$
Worst Case:
$T_{\text{worst sort}} (n) = T_{\text{worst sort}} (n-1) + T_{\text{worst insert}} (n-1)$
$T_{\text{worst sort}} (n) = 1+\sum_{i=1}^{n-1} (3i+1) = 1 + 3 \sum_{i=1}^{n-1} i + \sum_{i=1}^{n-1} 1$
$= 1 + \frac{3(n(n-1))}{2} + n - 1$
$T_{\text{worst sort}} \in O(n^2)$
$M_{\text{worst sort}} \in O(n^2)$ (same as above)
$T_{\text{sort}} (n)$
| n | cost |
|---|---|
| 0 | 1 |
| >0 | $T_{\text{sort}} (n-1) + T_{\text{insert}} (n-1)$ |
$M_{\text{sort}} (n)$
| n | cost |
|---|---|
| 0 | 0 |
| >0 | $M_{\text{sort}} (n-1) + M_{\text{insert}} (n-1)$ |
Selection Sort
Recall that selection sort gets the minimum value and swaps it with the first of the list. Continues this until the entire list has been traversed.
Methods used:
swapfindMinIndexselectionSort
$T_{\text{swap}} (n) = 4$
$T_{\text{findMinIndex}} (n) = 3 + n(t_{\text{comp}} + 4)$
$T_{\text{selection sort}} (n) = n * ( n (t_{\text{comp}} + 4) + 3 + 4)$
$T_{\text{selection sort}} (n) \in O(n^2)$
But is this fair? The list shrinks as we look through it, so it’s not really $O(n^2)$.
Consider the term: $n * (n (t_{\text{comp}} + 4))$
$n(t_{\text{comp}} + 4) + (n-1) (t_{\text{comp}} + 4) + … + (n - n) (t_{\text{comp}} + 4)$
$= t_{\text{comp}} + 4 \sum_{i=0}^{n} i + …$
$= t_{\text{comp}} + 4 \frac{n (n+1)}{2}$
So yes, $O(n^2)$ is fair. Even when we reduce it, it still has the $n^2$. We do the same thing every time, there is no difference between the best and the worst case. There, however, are not objects being created (because it’s doing the swapping in place).
$T_{\text{selection sort}} (n) \in O(n^2)$
$T_{\text{selection sort}} (n) \in \Omega (n^2)$
Recall transitivity:
- if $a<b$ and $b<c$, then $a<c$.
Quicksort
Consider partitioning. If we pick a middle value, say, 4, and compare everything else to that number. We then can move all items greater than that number after it and those less than the number, we can move before it.
For example:
This:
| 4 7 6 2 5 0 3 1 |
Turns into this:
| 1 2 3 0 | 4 | 7 6 5 |
If we do this, we don’t need to compare the numbers on the left with the numbers on the right. This method is called Divide and Conquer.
We would call 4 the pivot. If we assume that the list is scrambled enough, we can just take the first item in the list as the pivot.
Quicksort:
- Choose a pivot
- Partition
- QuickSort by partitioning the left portion and partitioning the right portion
We do this by having a temporary list with a low index pointer (that starts the beginning of the pointer) and a high index pointer (that starts at the end of the list). You compare each item in the list with the pivot and if it is greater, you put it where high is pointing and decrement high. If it is less than, you put it where low is pointing and you increase low. Once high equals low, you are done and you just put the pivot where high (or low) is.
Quick Sort In Place:
while (low <= high) {
while(list.get(low) <= pivot) {
low++;
}
while(list.get(high) > pivot) {
high--;
}
if (low < high) {
swap(list, low, high);
}
}
We move the low and high until the low is greater than the pivot and high is less than the pivot. We now know that we should swap them. Once this is done, we know that low = high and the pivot should be placed right before low (or high).
Full Code:
// In ArrayUtils
// EFFECT: Sorts the given ArrayList according to the given comparator
<T> void quicksort(ArrayList<T> arr, IComparator<T> comp) {
quicksortHelp(arr, comp, 0, arr.size());
}
// EFFECT: sorts the source array according to comp, in the range of indices [loIdx, hiIdx)
<T> void quicksortHelp(ArrayList<T> source, IComparator<T> comp,
int loIdx, int hiIdx) {
// Step 0: check for completion
if (loIdx >= hiIdx) {
return; // There are no items to sort
}
// Step 1: select pivot
T pivot = source.get(loIdx);
// Step 2: partition items to lower or upper portions of the temp list
int pivotIdx = partition(source, comp, loIdx, hiIdx, pivot);
// Step 3: sort both halves of the list
quicksortHelp(source, comp, loIdx, pivotIdx);
quicksortHelp(source, comp, pivotIdx + 1, hiIdx);
}
// Returns the index where the pivot element ultimately ends up in the sorted source
// EFFECT: Modifies the source list in the range [loIdx, hiIdx) such that
// all values to the left of the pivot are less than (or equal to) the pivot
// and all values to the right of the pivot are greater than it
<T> int partition(ArrayList<T> source, IComparator<T> comp,
int loIdx, int hiIdx, T pivot) {
int curLo = loIdx;
int curHi = hiIdx - 1;
while (curLo < curHi) {
// Advance curLo until we find a too-big value (or overshoot the end of the list)
while (curLo < hiIdx && comp.compare(source.get(curLo), pivot) <= 0) {
curLo = curLo + 1;
}
// Advance curHi until we find a too-small value (or undershoot the start of the list)
while (curHi >= loIdx && comp.compare(source.get(curHi), pivot) > 0) {
curHi = curHi - 1;
}
if (curLo < curHi) {
swap(source, curLo, curHi);
}
}
swap(source, loIdx, curHi); // place the pivot in the remaining spot
return curHi;
}
$T_{\text{qs}} (n) = P(n) + T_{\text{qs}} (i) + T_{\text{qs}} (n-i-1)$
Swaps
- Best case: No swaps
- Worst case: Swap each time, $\frac{n}{2}$ swaps
We know, by this, that the partitions are linear.
$T_{\text{qs}} (n) = T_{\text{qs}} (i) + T_{\text{qs}} (n-i-1) + c_1 n$
Worst Case:
$T_{\text{qs}} (n) = T (n-1) + c_1 n$
$= T(n-2) + c_1 n + c_1 n$
$= T(n-(n-1)) + (n-1) n c_1$
$T_{\text{qs}} \in O(n^2)$
Best Case:
$T_{\text{qs}} (n) = T_{\text{qs}} (\frac{n}{2}) + T_{\text{qs}} (\frac{n}{2}) + c_1 n$
$= 2T_{\text{qs}} (\frac{n}{2}) + c_1 n$
$= [2 (2 T_{\text{qs}} (\frac{n}{4})) + c_1 \frac{n}{2}] + c_1 n$
$= 2^2 (T (\frac{n}{2^2}) + c_1 \frac{n}{2}) + c_1 n$
$= 2^i T (\frac{n}{2^i}) + i c_1 n$
We want to know when $\frac{n}{2^i} = 1$ (which is the base case)
$n = 2^i$
$\therefore i = \log_{2} n$
$= 2^{\log_2 (n)} T (\frac{n}{2^{\log_{2} n}} ) + \log_{2} n c_1$
$= n T_{\text{qs}} (1) + c_1 n \log_{2} n$
$T_{\text{qs}} (n) \in \Omega (n \log_{2} n)$
(And it’s done in place so it doesn’t take up any space)
Mergesort
Consider the list:
| 4 7 6 5 3 0 1 |
Sort pairs of numbers:
| 47 | 56 | 03 | 1 |
Merge:
| 4 5 6 7 | 0 1 3 |
| 0 1 3 4 5 6 7 |
Note: you don’t have to compare every element to every other element if we know that each sub-list is sorted.
We can also do this in place. By advancing a low and high.
$T_{ms} (n) = 2T_{ms} (\frac{n}{2}) + T_{merge} (n)$
$T_{ms} (n) = \Omega (n \log_2 n) + O(n)$
But no matter what the list is, we are always doing the same amount of comparisons. Although this is more consistent than quicksort, we do use space (holding onto the split lists).
What we saw:
- insertion sort
- Easy to code
- Worst case: $O(n^2)$, $\Omega (n)$ (but on average is better)
- selection sort
- Didn’t take any space
- Always $O(n^2)$, $\Omega (n^2)$
- quick sort
- $O(n^2)$, $\Omega (n \log_2 n)$
- merge sort
- $O(n \log_2 n)$, $\Omega (n \log_2 n)$
- ?
- $O(n \log_2 n)$, $\Omega (n \log_2 n)$ with no extra space
Exam 2 - Second Practice Test
- What is the difference between an abstract class and an interface?
- What is the difference between
superandthis? - Consider the following code and complete the method:
// Represents a Shape
interface IShape {
// Create this method
boolean sameShape(IShape other);
}
class Rect implements IShape {
int height;
int width;
Rect(int height, int width) {
this.height = height;
this.width = width;
}
}
class Circle implements IShape {
int size;
Circle(int size) {
this.size = size;
}
}
-
Create the data structures for
PaintingsandArtists. Any definition would be acceptable as long as you can get theArtistfrom aPaintingand vice versa. - What is the difference between
for-each,counted-for, andwhileloops?- When are each good (and bad) options?
- Consider the following code and complete the methods:
interface IList<T> {
// Create this method
IList<T> filter(Predicate<T> pred);
// Create this method
<U> IList<U> map(Function<T, U> func);
// Create this method
<U> U fold(BiFunction<T, U, U> f, U base);
}
class ConsList<T> implements IList<T> {
T first;
IList<T> rest;
ConsList(T first, IList<T> rest) {
this.first = first;
this.rest = rest;
}
}
class MtList<T> implements IList<T> {
}
- With the following code, (1) create a method that calculates the area of a shape using Visitors, (2) create a method that grows a shape by a given value using Visitors:
interface IShape {
// Create this method
boolean sameShape(IShape other);
}
class Rect implements IShape {
int height;
int width;
Rect(int height, int width) {
this.height = height;
this.width = width;
}
}
class Circle implements IShape {
int size;
Circle(int size) {
this.size = size;
}
}
- Redo your code from the
IListquestion above and have all of the methods Visitors. - Fill in the check expects below:
class Counter {
int val;
Counter() {
this(0);
}
Counter(int initialVal) {
this.val = initialVal;
}
int get() {
int ans = this.val;
this.val = this.val + 1;
return ans;
}
}
class ExamplesCounter {
boolean testCounter(Tester t) {
Counter c1 = new Counter();
Counter c2 = new Counter(5);
Counter c3 = c1;
// What should these tests be?
return t.checkExpect(c1.get(), ___)// Test 1
&& t.checkExpect(c2.get(), ___)// Test 2
&& t.checkExpect(c3.get(), ___)// Test 2
&& t.checkExpect(c1.get() == c1.get(), ___)// Test 3
&& t.checkExpect(c2.get() == c1.get(), ___)// Test 4
&& t.checkExpect(c2.get() == c1.get(), ___) // Test 5
&& t.checkExpect(c1.get() == c1.get(), ___) // Test 6
&& t.checkExpect(c2.get() == c1.get(), ___)// Test 7
}
}
- Recall our definition of
Deque. Make it so that you can use our defined Deque objects in afor-eachloop. - Create an iterator for
Binary Search Treesthat traverses the tree in the order of its values. - Consider the following code. Fill in the checkExpect
// Assume that Book and Author are defined above with each holding a String _name_
Book book1 = new Book("Book1");
Author author1 = new Author("Author 1");
Map<Author, Book> map1 = new HashMap<Author, Book>();
map1.put(this.author1, this.book1);
t.checkExpect(map1.get(this.author1), ___);
t.checkExpect(map1.get(new Author("Author 1"), ___);
Reading the next sentence will give away the answer!!! Okay, so assuming that you’ve finished the problem, you should realize that the second checkExpect returns null. Why is that? Design what you need to to assure that the checkExpect returns what is desired – which is book1.
Priority Queues and Heapsort
We saw stacks (last in, first out) and queues (first in, first out).
How can we define priority queues? That is, something that the thing with the highest priority gets served first.
Which tree is better? Obviously the left because the max height is $\log_2 (n)$ if n is the number of nodes. Whereas the tree on the right is basically a list.
An invariant is something that never changes.
Max heap:
- Invariant 1 (Structural): the tree is full on every level, except the last one which is filled in from left to left to right.
- Invariant 2 (Logical): Every child of a node is less than the parent.
Example:
Upheap:
Add: $\in O(\log_2 (n))$
We want to add 36. Can we put it as the left child of the 1? No, it violates the second invariant. Place it there to satisfy the first invariant. Then so swap the 36 and 1 (when placed in the invalid location). Now, swap 36 with the 3 and we now have a valid heap.
Now, we want to add 48. Place as right child of 3. Swap 48 and 3. Swap 48 and 36.
The resulting tree is:
Downheap: Remove: $\in O(\log_2 (n))$
Remove 48. Place 3 (the last thing in the heap) where 48 was. This makes it structurally valid, but it still isn’t logically valid. Swap 3 with 36.
We now want to use an array-based structure instead of a tree. So we can give every node an index:
How can we get the children so that we can move it to an ArrayList?
- leftchild(i) = 2i + 1
- rightcild(i) = 2i + 2
- parent(i) = $\lfloor \frac{i-1}{2} \rfloor$ (integer math)
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Priority | 70 | 60 | 50 | 30 | 50 | 40 | 20 | 10 | 20 | 15 |
Now, let’s try to do add given this ArrayList representation. We first add it to the last position:
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Priority | 70 | 60 | 50 | 30 | 50 | 40 | 20 | 10 | 20 | 15 | 65 |
Get parent: $\lfloor \frac{10-1}{2} \rfloor = 4$. It’s greater than it’s parent so swap.
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Priority | 70 | 60 | 50 | 30 | 65 | 40 | 20 | 10 | 20 | 15 | 50 |
Get parent again (which is index 1). It’s greater than it’s parent so swap again.
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Priority | 70 | 65 | 50 | 30 | 60 | 40 | 20 | 10 | 20 | 15 | 50 |
The parent of 1 (which is 0) is greater so we are done.
What about deleting? Let’s go back to our original list:
We remove the 70 and replace it with the last in the list.
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Priority | 15 | 60 | 50 | 30 | 50 | 40 | 20 | 10 | 20 | 70 |
Our heap ends at 8, but we are just putting the 70 at the end temporarily.
Because the largest child is greater, we swap the 15 and the 60.
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Priority | 60 | 15 | 50 | 30 | 50 | 40 | 20 | 10 | 20 | 70 |
We then look at the largest child of 1 which is 4 and we see that it’s greater so we swap.
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Priority | 60 | 50 | 50 | 30 | 15 | 40 | 20 | 10 | 20 | 70 |
4 is greater than or equal to its children so we are done.
What if we remove 60?
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Priority | 50 | 10 | 40 | 30 | 15 | 20 | 20 | 10 | 60 | 70 |
Now remove 50?
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Priority | 50 | 30 | 40 | 10 | 15 | 20 | 20 | 50 | 60 | 70 |
See the pattern? At the end of the heap, we are sorting things least to greatest. Say we remove everything from the heap, we would end up with a sorted list. We would end up with a sorted list using heapsort.
Heapsort
Steps for heapsort:
- Build a valid heap
- Remove all elements from the heap $\in O(n \log_2 n)$ (we saw the removing one element is $\log_2 (n)$ and we do this n times)
What is the Big O for building the heap?
| 13 | 14 | 18 | 17 | 12 | 16 | 11 | 10 |
We can just start with the first element and continue adding. This would be $O(n \log_2 (n))$
But there is a more efficient way to build the tree. We can first build an invalid tree. Then start with the last element (that has leaves as children) and do upheap.
(size of the array list - 1) / 2
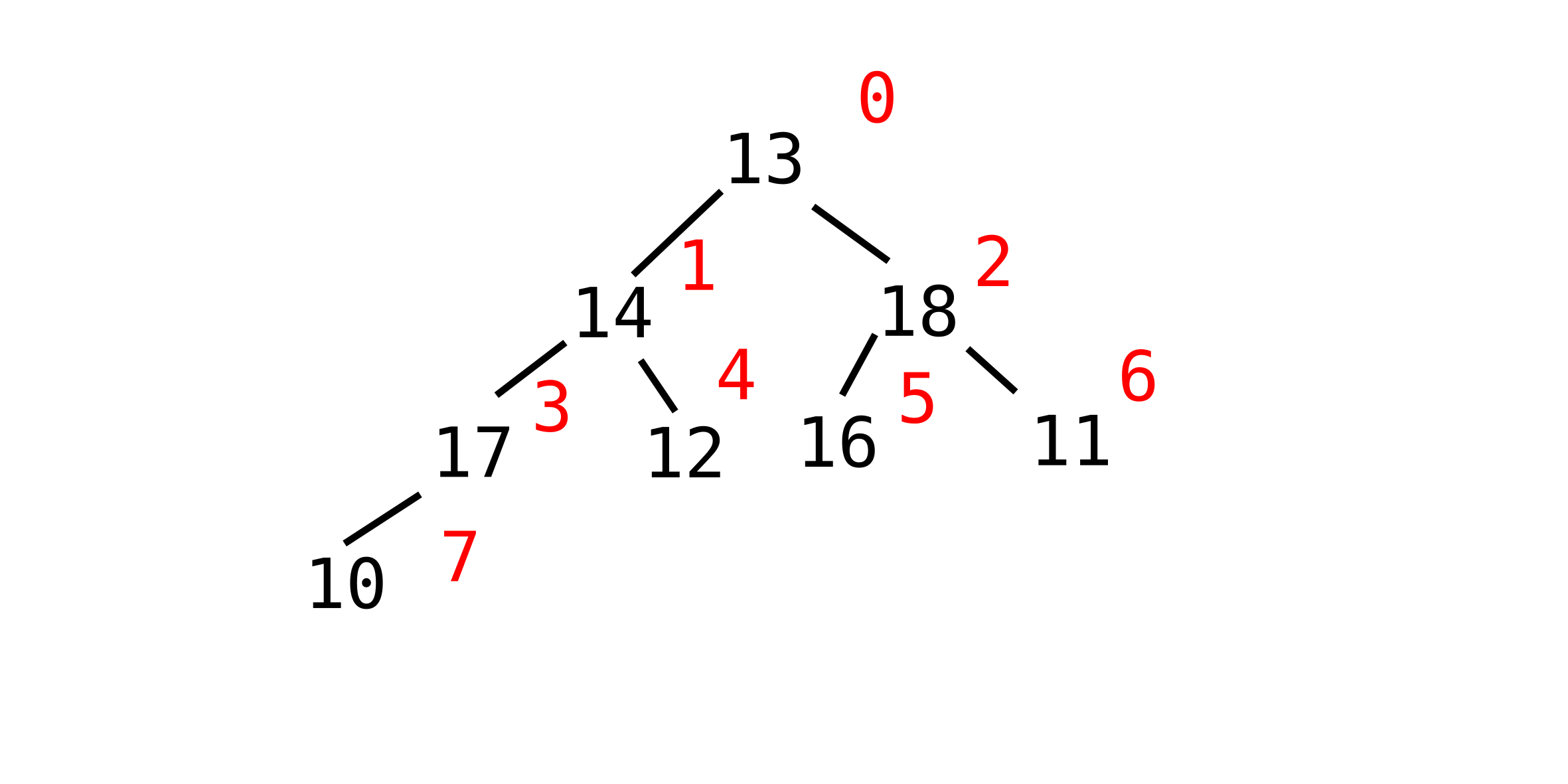
We are then left with another valid heap (slightly different than the first one, however). This is less than $O(n \log_2 (n))$ so heapsort as a whole is $O(n \log_2 (n))$.
Heapsort: $O(n \log_2 n)$ and $\Omega (n \log_2 n)$ and it doesn’t take up any extra space (because you can represent heaps as lists).
Breadth-first Search and Depth-first Search on Graphs
Graphs you can have connections from one node to any other node. Road maps/flight maps/social network are good examples of graphs.
A node looks like:
Undirected graph:
Nodes can also be called vertices. Connections can also be called edges.
Directed graph:
We can also make an undirected graph from a directed graph (by also having arrows going the other way).
You can also assign costs to connections. When we have costs, it’s called a weighted graph. (And we can make a weighted graph unweighted by assigning the same weight to every connection.)
Consider
And then we can have a table to represent the cost between different nodes:
Adjacency Matrix:
| x | 0 | 1 | 2 |
| 0 | 0 | 2 | 3 |
| 1 | -1 | 0 | 4 |
| 2 | -1 | 5 | 0 |
// Represents the above table
ArrayList<ArrayList<Integer>> graph;
graph.get(i).get(j)
But this isn’t very efficient.
Another representation that we can use is an Adjacency List.
class Vertex {
String name;
ArrayList<Edge> outEdges;
Vertex(String name, ArrayList<Edge> outEdges){
this.name = name;
this.outEdges = outEdges;
}
// is there a path from this vertex to the given one?
boolean hasPathTo(Vertex dest, ArrayList<Vertex> seen) {
for (Edge e : this.outEdges) {
if (!seen.contains(e.to)) {
seen.add(e.to);
if ( e.to == dest // can get there in just one step
// can get there on a path through e.to
|| e.to.hasPathTo(dest, seen)) {
return true;
}
}
}
return false;
}
}
class Edge {
Vertex from;
Vertex to;
int weight;
Edge(Vertex from, Vertex to, int weight) {
this.from = from;
this.to = to;
this.weight = weight;
}
}
class Graph {
ArrayList<Vertex> allVertices;
Graph(ArrayList<Vertex> verts) {
this.allVertices = verts;
}
}
Now, something that we can ask is “is there a connection between these two given nodes?”. Recall that we used an accumulator to keep track of the already visited nodes (so we don’t get stuck in a loop).
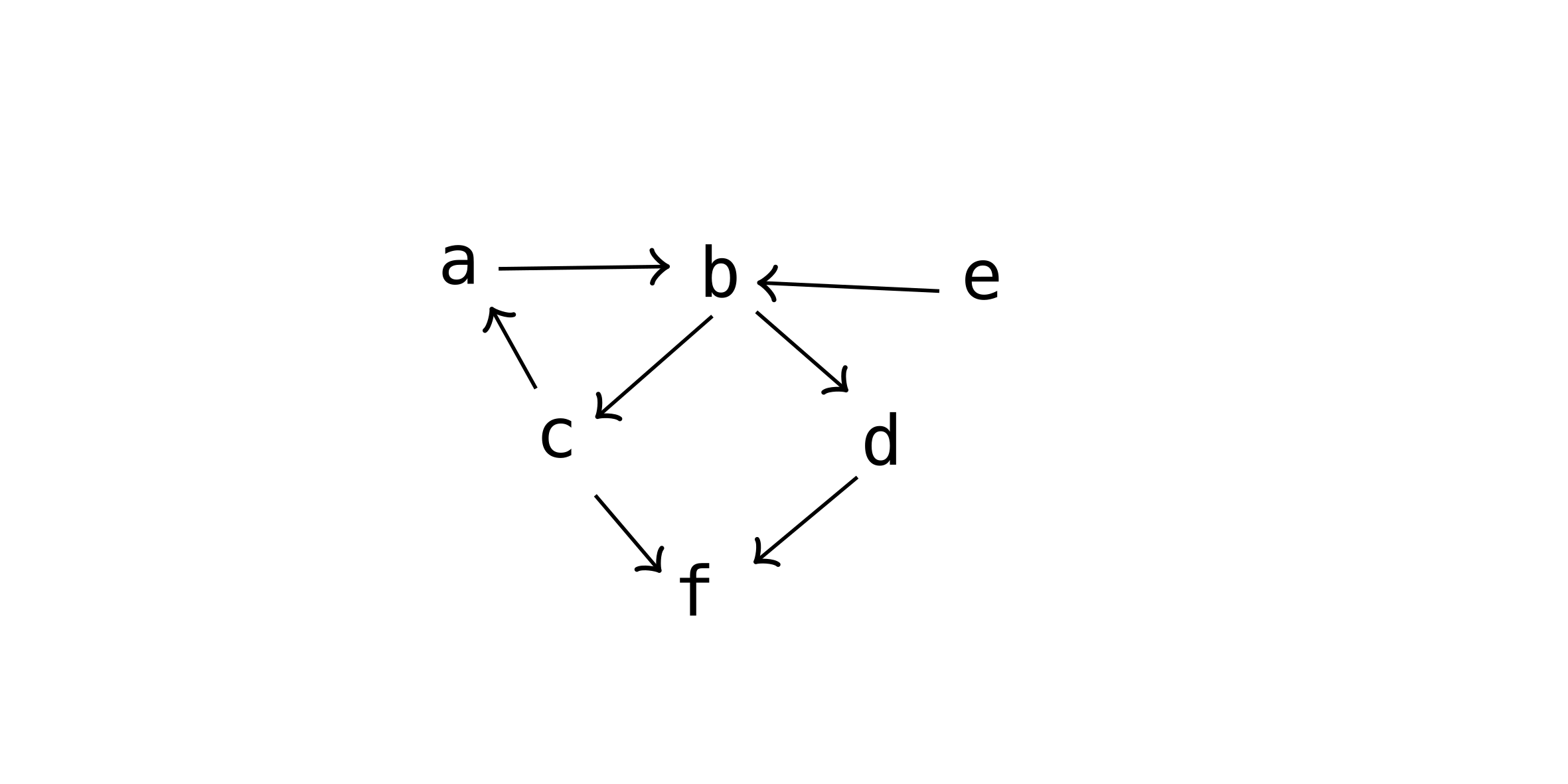
Say we want to go from a to e. Can we do it? (At a glance we can see that it’s no, but how would we do this in code?) Make sure that you keep track of what nodes you’ve already visited.
Depth-first traversal (go as far as you can down one path).
- a, b, c, f, a, d, f
Breadth-first traversal
- a, b, c, d, a, f
// in Graph class
// is there a path from node _from_ to node _to_ in this graph using DFS?
boolean hasPathDFS(Vertex from, Vertex to) {
// Stack: Last in, first out
ArrayList<Vertex> alreadySeen = new ArrayList<Vertex>();
Deque<Vertex> worklist = new Deque<Vertex>();
worklist.addAtHead(from);
while(worklist.size() > 0) {
Vertex next = worklist.removeFromHead();
// We can use intentional equality because we are
// looking for the exact node. Did we find the ~exact~
// thing we were looking for?
if (next == to) {
return true;
}
else if (alreadySeen.contains(next)) { }
else {
for (Edge e : next.outEdges) {
worklist.addAtHead(next);
}
alreadySeen.add(next);
}
}
return false;
}
// is there a path from node _from_ to node _to_ in this graph using BFS?
boolean hasPathBFS(Vertex from, Vertex to) {
// Queue: First in, first out
ArrayList<Vertex> alreadySeen = new ArrayList<Vertex>();
Deque<Vertex> worklist = new Deque<Vertex>();
// Changed line
worklist.addAtTail(from);
while(worklist.size() > 0) {
Vertex next = worklist.removeFromHead();
// We can use intentional equality because we are
// looking for the exact node. Did we find the ~exact~
// thing we were looking for?
if (next == to) {
return true;
}
else if (alreadySeen.contains(next)) { }
else {
for (Edge e : next.outEdges) {
// Changed line
worklist.addAtTail(next);
}
alreadySeen.add(next);
}
}
return false;
}
Both these functions look very similar so we can abstract them.
interface ICollection<T> {
// Gets the size of the collection
int size();
// Adds a given item to the collection
void add(T t);
// Removes the item at the front
T remove();
}
class Stack<T> implements ICollection<T> {
Deque<T> items;
Stack() {
this.items = new Deque<T>();
}
// Gets the size of the collection
public int size() {
return this.items.size();
}
// Adds a given item to the collection
public void add(T t) {
this.items.addAtHead(t);
}
// Removes the item at the front
public T remove() {
return this.items.removeFromHead();
}
}
class Queue<T> implements ICollection<T> {
Deque<T> items;
Queue() {
this.items = new Deque<T>();
}
// Gets the size of the collection
public int size() {
return this.items.size();
}
// Adds a given item to the collection
public void add(T t) {
this.items.addAtTail(t);
}
// Removes the item at the front
public T remove() {
return this.items.removeFromHead();
}
}
Now we can rewrite our hasPath methods:
// Is there a path between _from_ and _to_?
boolean hasPath(Vertex from, Vertex to, ICollection<Vertex> worklist) {
// Queue: First in, first out
ArrayList<Vertex> alreadySeen = new ArrayList<Vertex>();
worklist.add(from);
while(worklist.size() > 0) {
Vertex next = worklist.remove();
// We can use intentional equality because we are
// looking for the exact node. Did we find the ~exact~
// thing we were looking for?
if (next == to) {
return true;
}
else if (alreadySeen.contains(next)) { }
else {
// To avoid field-of-a-field, put this for loop in the Vertex class
for (Edge e : next.outEdges) {
worklist.add(next);
}
alreadySeen.add(next);
}
}
return false;
}
// is there a path from node _from_ to node _to_ in this graph using DFS?
boolean hasPathDFS(Vertex from, Vertex to, ICollection<Vertex> worklist) {
return this.hasPath(from, to, new Stack<Vertex>());
}
// is there a path from node _from_ to node _to_ in this graph using BFS?
boolean hasPathBFS(Vertex from, Vertex to, ICollection<Vertex> worklist) {
return this.hasPath(from, to, new Queue<Vertex>());
}
Consider the graph:

Path from b to e?
DFS
- worklist:
b,c(added after d),f(added after a),a(added after c),d,f - alreadyseen: b, c, f, a
- next:
b,c,f,a,b,d,f
Nothing else on the worklist and it was never found, so return false.
Minimum Spanning Trees
Consider the graph:
We want to keep the vertices but get rid of the unnecessary edges.
Options:
These are called spanning trees.
Now, what if we have weights on the edges? We then want the spanning tree with the least cost. This is called the minimum spanning tree.
Consider
The minimum spanning tree for the graph of the left is the graph on the right.
For n nodes, the minimum spanning tree will have n-1 edges.
We have algorithms for this:
Prim’s Algorithm
To find the minimum spanning tree T:
- Choose any node to be in
T - Consider which edges in
Tconnect to nodes outside ofT- Choose one with the minimum weight. Add the edge to
Tas long as it does not introduce any cycles.
- Choose one with the minimum weight. Add the edge to
- Repeat step 2, until every node is in
Tor you haven-1edges.
Pseudo code:
// The final resulting tree
ArrayList<Edge> tree = new ArrayList<Edge>();
// The set of connected vertices
HashMap<Vertex, Boolean> connected = new HashMap<Vertex, Boolean>();
// The priority queue of candidate edges
PriorityQueue<Edge> frontier = new PriorityQueue<Edge>();
If the graph's vertices are empty, just return the empty tree
Initialize the connected map to map each vertex to false
Pick some initial vertex, v. Set its connectedness to true, and add
all its edges to the frontier.
While(the frontier is not empty)
Pick the cheapest edge from the frontier, suppose it connects X to Y.
If Y is already connected to the tree:
Discard this edge // it would create a cycle
Else:
Add the edge XY to the tree
Mark Y as connected
Add all the out-edges of Y to the frontier
Return the tree
Kruskal’s Algorithm
Steps:
- Find the cheapest edge and mark it
- Find the next cheapest unmarked edge that does not create a cycle
- Repeat step 2 until
n-1edges
Cost (Big O):
- Sort all of the edges by weight
- Look for cycles
For looking for cycles, we can use Union-find.
Union-find:
Maintains a partition of objects
find(x) - returns the name of the group that x belongs to.
union(x, y) - Takes the names of two groups and fuses (unions) them into one group.
Objects: nodes
Groups: Connected components with respect to currently chosen edges
Consider the graph:
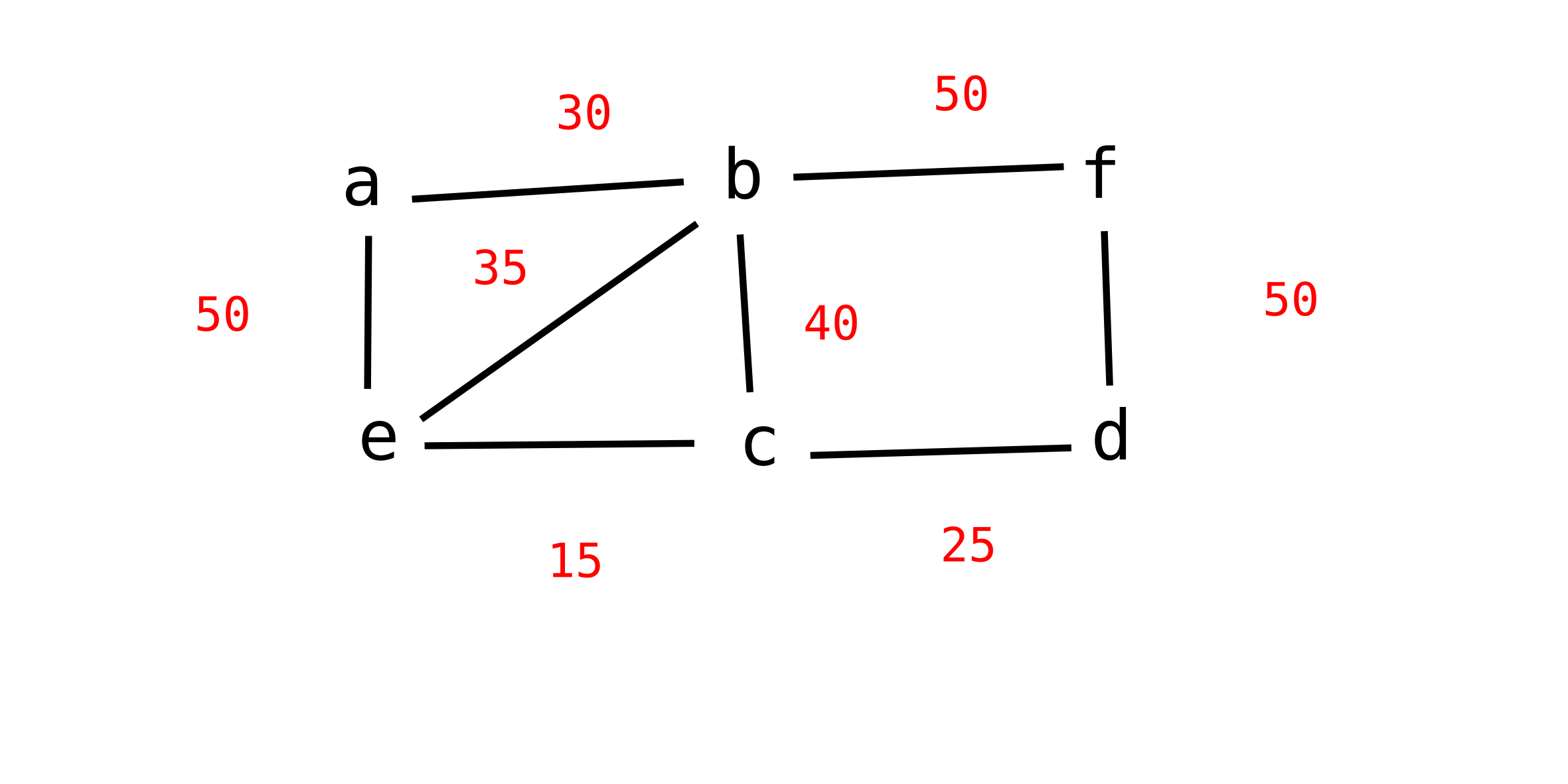
| Nodes | A | B | C | D | E | F |
| Representative | C |
Groups:
| C | |||||
|---|---|---|---|---|---|
| E, D, A, B, F |
Pseudo code:
HashMap<String, String> representatives;
List<Edge> edgesInTree;
List<Edge> worklist = all edges in graph, sorted by edge weights;
initialize every node's representative to itself
While(there's more than one tree)
Pick the next cheapest edge of the graph: suppose it connects X and Y.
If find(representatives, X) equals find(representatives, Y):
discard this edge // they're already connected
Else:
Record this edge in edgesInTree
union(representatives,
find(representatives, X),
find(representatives, Y))
Return the edgesInTree
Dijkstra’s Algorithm for Single-Source Shortest Paths
Say you want to take a flight with the least amount of money or shortest flight time.
Recall our Vertex definition from last lecture. A Graph has a list of vertices.
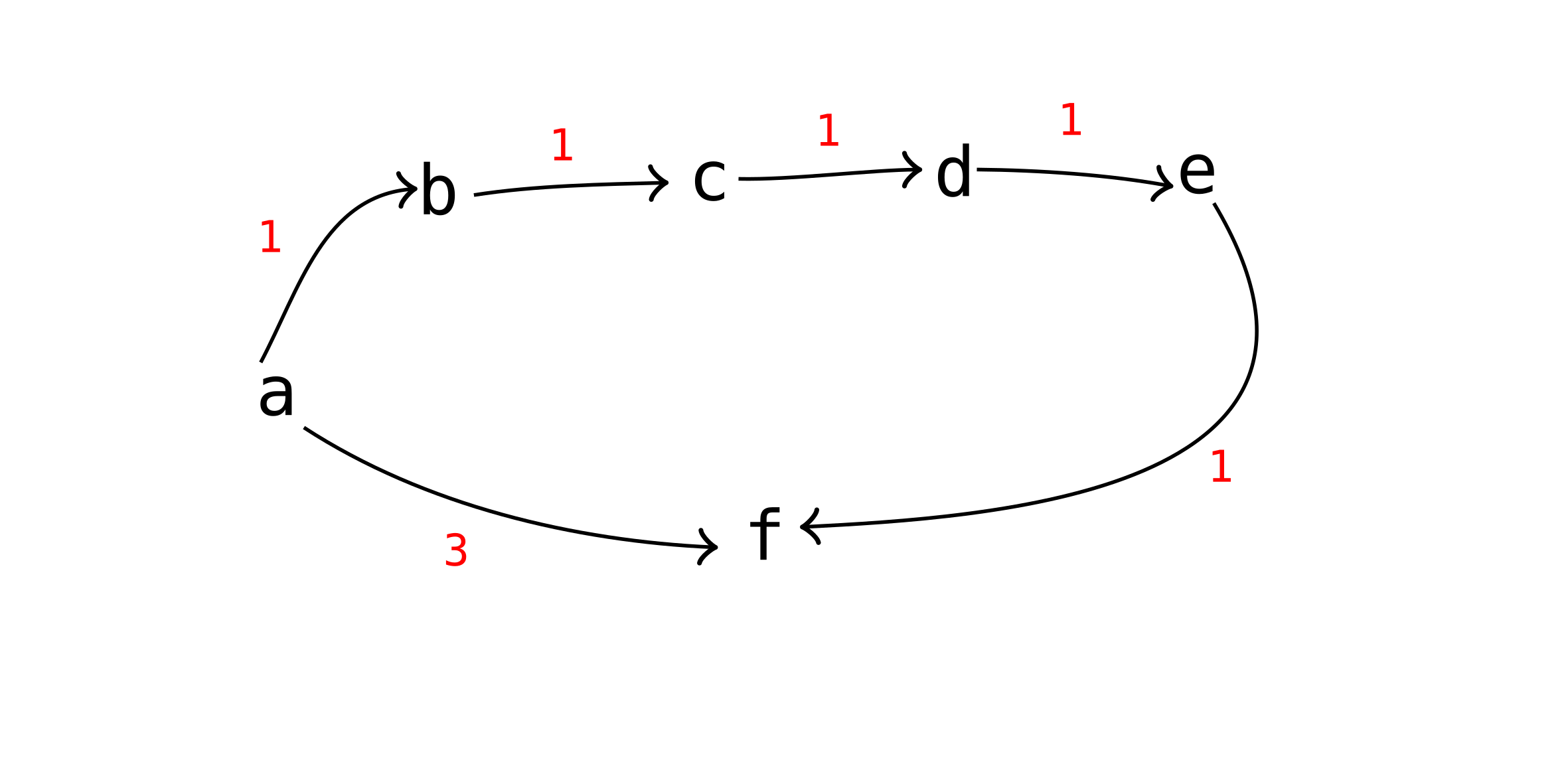
| Worklist | - |
|---|---|
| a(0) | |
| b(1) | f(3) |
| c(1) | f(3) |
| d(1) | f(3) |
| e(1) | f(3) |
| f(1) | f(3) |
Cost of a->b->c->d->e->f = 5
But we can just from a->f = 3
Instead, we keep track of how much it costs to get to any given point as you are traversing. This is called Dijkstra’s Algorithm.
Consider this graph:
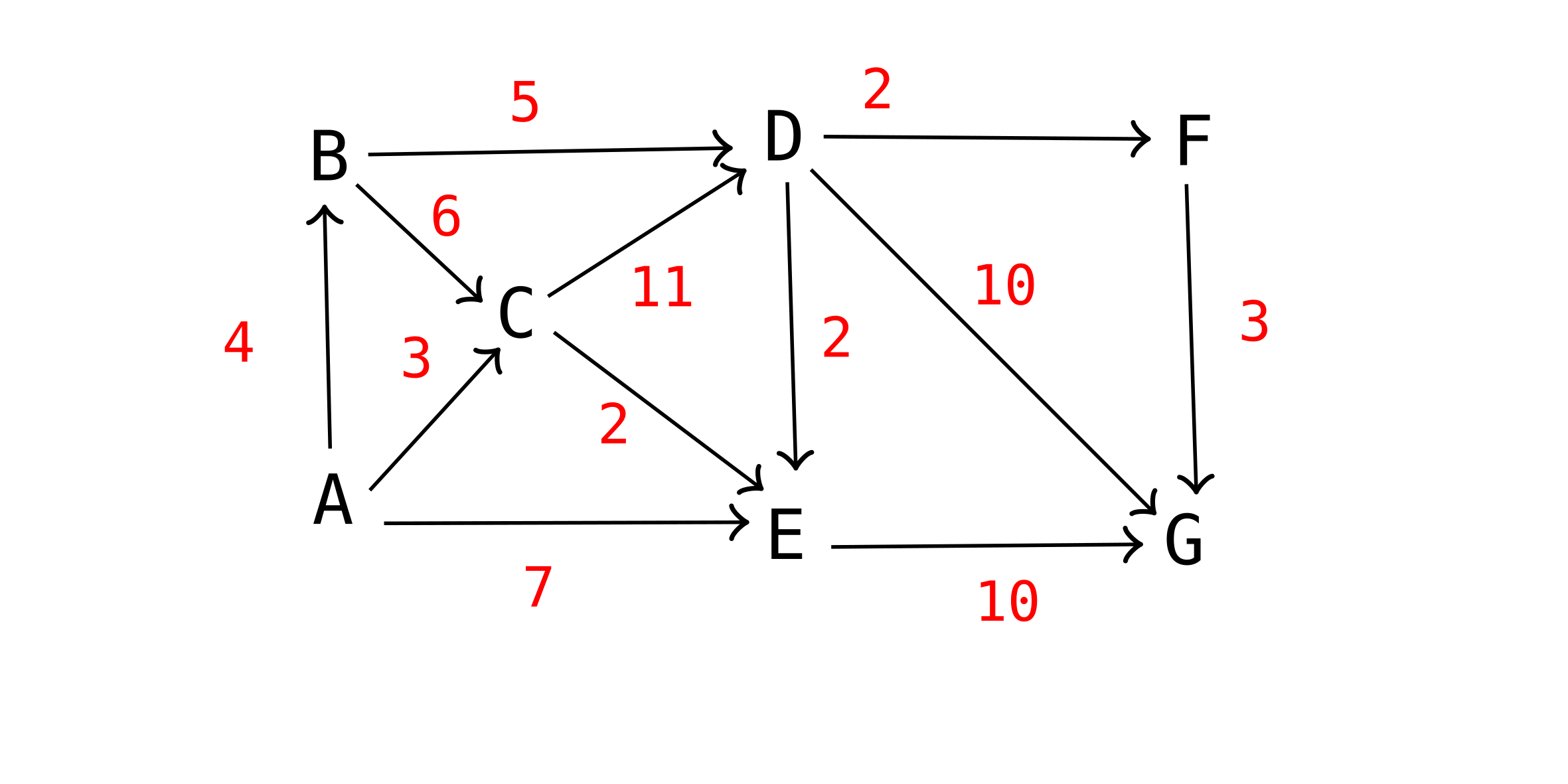
We want the cheapest path from a to g.
Dikstra’s Shortest Path
- Set the distances at each node to $\infty$
- Set the start node’s distance to 0
- If there are any unvisited nodes left, select the next node and remove from unvisited. Call it
v. - Look at all of the edges coming out of
v. For each edge, do the following:- Compute D(v) (distance to get to v) + weight(v, n) = c (the cost)
- If
cis less than D(n), then there is a cheaper way to get ton(throughv). Update D(n) to bec.
- Repeat step 3, as long as there are unvisited nodes
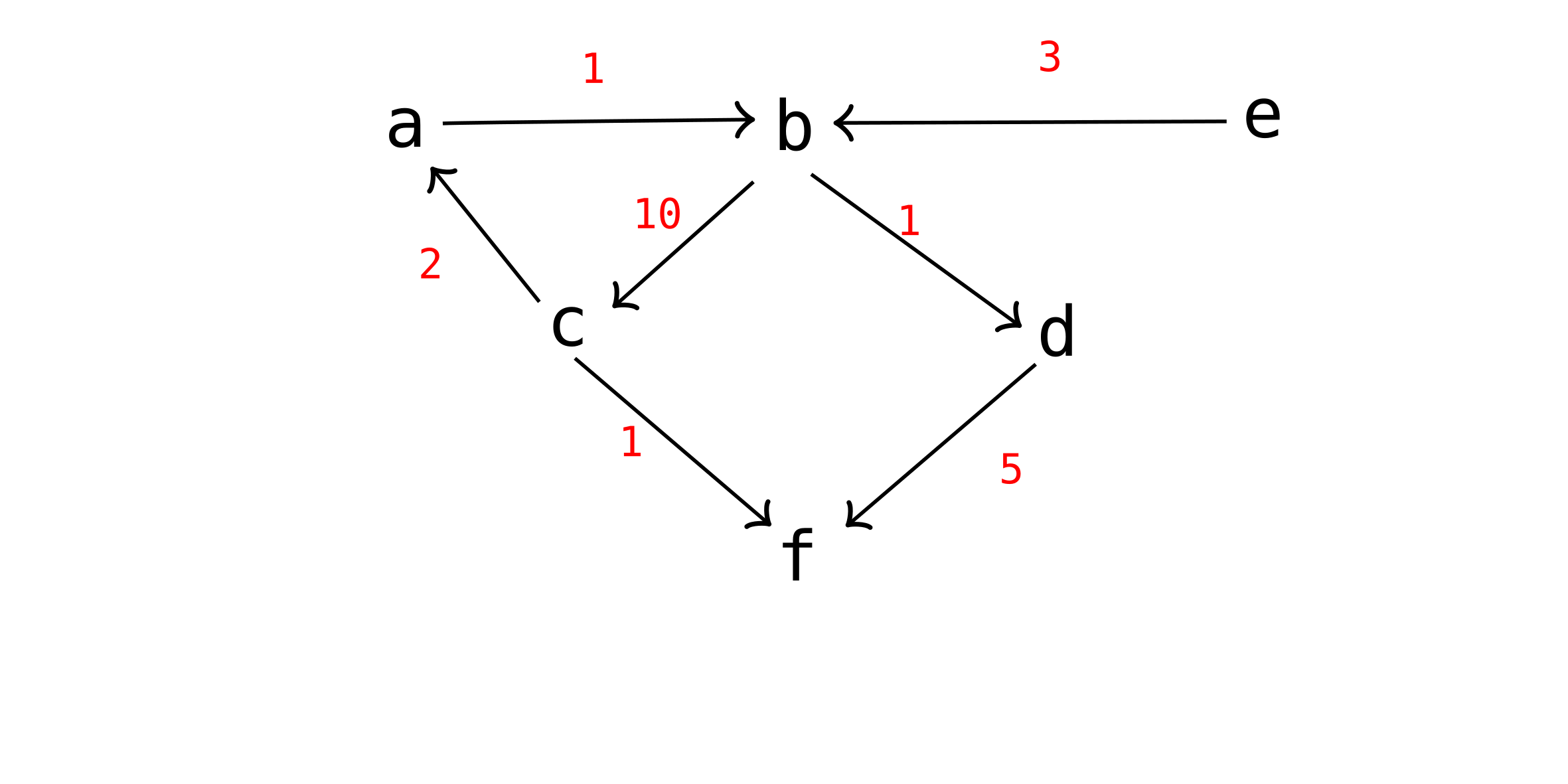
// In graph class
// Find the cost of the cheapest path between the two given vertices
int shortestPath(Vertex source, Vertex target) {
ArrayList<Vertex> unvisited = new ArrayList<Vertex>();
HashMap<Vertex, Integer> distances = new HashMap<Vertex, Integer>();
HashMap<Vertex, Vertex> predecessors = new HashMap<Vertex, Vertex>();
unvisited.add(source);
distances.put(source, 0);
while(unvisited.size() > 0) {
Vertex v = unvisted.remove(0);
// You can also use a priority queue here
for (Edge e : v.outEdges) {
if (distances.get(e.to) == null || distances.get(e.to) > distances.get(v) + e.weight) {
distances.put(e.to, distances.get(v) + e.weight);
predecessors.put(e.to, v);
unvisited.add(e.to);
}
}
}
if (distances.get(target) == null) {
return -1;
} else {
return distances.get(target);
}
}
// Find the cheapest path between the two given vertices
ArrayList<Vertex> shortestPath(Vertex source, Vertex target) {
ArrayList<Vertex> unvisited = new ArrayList<Vertex>();
HashMap<Vertex, Integer> distances = new HashMap<Vertex, Integer>();
HashMap<Vertex, Vertex> predecessors = new HashMap<Vertex, Vertex>();
unvisited.add(source);
distances.put(source, 0);
while(unvisited.size() > 0) {
Vertex v = unvisted.remove(0);
// You can also use a priority queue here
for (Edge e : v.outEdges) {
if (distances.get(e.to) == null || distances.get(e.to) > distances.get(v) + e.weight) {
distances.put(e.to, distances.get(v) + e.weight);
predecessors.put(e.to, v);
unvisited.add(e.to);
}
}
}
ArrayList<Vertex> path = new ArrayList<Vertex>();
Vertex step = target;
if (predecessors.get(step) == null) {
return path;
}
path.add(step);
while (step != source) {
step = predecessors.get(step);
path.add(0, predecessors.get(step));
}
return path;
}
Recap
What are the languages we’ve seen so far?
Racket (up to ISL):
- Functional language
- Didn’t have to explicit in types. Therefore it is dynamically typed
Java:
- Object-oriented with classes
- Statically typed (have to declare types)
JavaScript:
- Object-oriented without classes
- Dynamically typed
Python:
- Objects with classes
- Dynamically typed
JavaScript
Doesn’t have anything to do with Java.
Less object-oriented than Java.
A lot more forgiving. This is good for web development
Operates like DrRacket’s interactive window
35 // Returns 35
true // Returns true
"hello" + 25 //Returns "hello25"
42 + "hello" // Returns "42hello"
"hello" + true // Returns "hellotrue"
"hello" + false // Returns "hellofalse"
[1, 2, 3] // Creates an Array
[1, 2, 3].length // 3
function f(x) {return x+2;}
f(2) // 4
Objects operate like dictionaries
var obj = {"x": 4, "a": "hello"}
obj.x // 4
obj.a // "hello"
Functions
function CatMaker(name) {this.name = name; this.sound = "meow"}
// This looks like a constructor
var fluffly = new CatMaker("fluffy")
fluffy // is type CatMaker
fluffy.name // "fluffy"
fluffy.sound // "meow"
// Create an object just like Fluffy but the only thing that's different is name
// __proto__ means gets everything else from fluffy
var fluffler = {name: "fluffier", __proto__: fluffy}
// It is now linked to Fluffy -- inheritance
fluffier.sound // "meow"
fluffy.sound = "purr"
fluffier.sound // "purr"
fluffier.snack = "tuna"
fluffy.snack // undefined -- doesn't go both ways
Object-orientation
Features of an object-oriented language
- Objects
- Fields/properties
- Methods
- Arguments
- Inheritance
- Constructors
- Dynamic dispatch
this(an object needs to know about itself)- Overriding methods
Building an object-oriented language in ISL
;; An Object is what it has
;; An Object is a [List-of PropVal]
;; A PropVal is a (list Name Value)
;; A Name is Symbol
;; A Value is a Number
(define mypos1 (list (list 'x 3) (list 'y 4)))
(define mypos2 (list (list 'x 6) (list 'y 8)))
;; access the property of a given Object
(define (dot obj prop)
(cond [(empty? obj) (error "prop is not defined")]
[else (if (symbol=? (first (first obj)) prop)
(second (first obj))
(dot (rest obj) prop))]))
(check-expect (dot mypos1 'x) 3)
(check-expect (dot mypos2 'y) 8)
Interfaces
- Tell what an object can do – not what it has
;; Change our definition of Object
;; An Object is what it does
;; An Object is [Itself Name Params -> Value]
;; A Params is a [List-of Value]
;; parents of all of the objects
(define object
(lambda (prop args) (error prop "Property is not defined")))
;; In here, you can also have methods that every object would have
;; such as toString
(define mypos1
(lambda (prop)
(cond [(symbol=? 'x prop) 3]
[(symbol=? 'y prop) 4]
[else (error prop "Property is not defined")])))
(define mypos1
(lambda (prop)
(cond [(symbol=? 'x prop) 6]
[(symbol=? 'y prop) 8]
[else (error prop "Property is not defined")])))
;; Produce the property of the given object
(define (dot obj prop args)
(obj obj prop args))
(check-expect (dot mypos1 'x) 3)
(check-expect (dot mypos2 'y) 8)
; We should have a constructor
;; constructs a 2d position
(define (make-pos x y)
(local [(define super object)]
(lambda (this prop args)
(cond [(symbol=? 'x prop) x]
[(symbol=? 'dist-to-0 prop)
(sqrt (+ (sqr x) (sqr y)))]
[(symbol=? 'y prop) y]
[(symbol=? 'closer-than prop)
(local [(define that (first args))]
(< (dot this 'dist-to-0 '())
(dot that 'dist-to-0 '())))]
[else (dot super prop args)]))))
;; constructs a 3d position
;; Represents inherintence
(define (make-pos-3d x y z)
(local [(define super (make-posn x y))
(lambda (this prop args)
(cond [(symbol=? 'z prop) z]
; Overriding
[(symbol=? 'dist-to-0 prop) (sqrt (+ (sqr x) (sqr y) (sqr z)))]
[else (dot (super this prop args))]))))
;; This will use the 'dist-to-0 method from the super class (i.e. make-pos)
(define my3dpos (make-pos-3d 3 4 12))
(define cmypos1 (make-pos 3 4))
(define cmypos2 (make-pos 3 8))
;; The tests will still pass
(check-expect (dot cmypos1 'x '()) 3)
(check-expect (dot cmypos2 'y '()) 8)
(check-error (dot cmypos1 'z '()) "z: Property is not defined")
(check-expect (dot my3dpos 'z '()) 12)
(check-expect (dot cmypos1 'dist-to-0 '()) 5)
(check-expect (dot cmypos2 'dist-to-0 '()) 10)
(check-expect (dot my3dpos 'dist-to-0 '()) 13)
(check-expect (dot mypos1 'closer-than (list mypos2)) #true)
(check-expect (dot mypos2 'closer-than (list my3dpos)) #true)
(check-expect (dot my3dpos 'closer-than (list mypos2)) #false)
Getting Ready for OOD (Object Oriented Design)
Recall IShape from Lecture 4.
The homeworks are bigger. Organize your code so it’s easier to read.
- Don’t have all of your code in one file
- Every class and interface should be in its own file
When you get to a lot of classes (i.e. there have been projects with 60+ classes). To manage this, we use Packages. So in our example, we would have a Shape Package which holds the IShape, Square, and Circle files. Then put CartPt in a Utils package.
We now need to make these interfaces and classes (and their constructors) Public (makes it visible to other things in other packages). And fields-of-fields don’t work so you need to either delegate or create getters.
We also make all of our fields private so that other things can’t access them.
// In Circle class
private CartPt center;
private int radius;
private String color;
We will also be moving to JUnit
- Add JUnit 4 to your path
import java.junit.Test;
// in ~public~ examples class
@Test
public void testCircleBigger() {
assertEquals(false, this.c1.biggerThan(this.c2));
assertEquals(true, this.c2.biggerThan(this.c1));
assertEquals(false, this.c1.biggerThan(this.s1));
assertEquals(false, this.c1.biggerThan(this.c2));
assertEquals(true, this.c1.biggerThan(this.s3));
// or:
assertFalse(this.c1.biggerThan(this.c2));
// You can also add messages to display if it goes wrong
assertTrue("c2 should be bigger than c1", this.c2.biggerThan(this.c1));
assertFalse(this.c1.biggerThan(this.s1));
assertFalse(this.c1.biggerThan(this.c2));
assterTrue(this.c1.biggerThan(this.s3));
}
For checkInexact, we also use assertEquals. For example:
// The last argument tells to use inexact comparison
assertEquals(this.s1.area(), 900.0, 0.01);
What about comparing objects? assertEquals uses .equals() so it defaults to intentional equality. Therefore, we need to override .equals().
// in Circle class
public boolean equals(Object o) {
if (o instanceof Circle) {
return (this.radius == ((Circle) o).radius)
} else {
return false;
}
}
// Always override hashCode as well
public int hashCode() {
return this.radius * 31;
}
// in Examples class
@Test
public void testCircleGrow() {
// assertEquals uses .equals()
assertEquals(this.c1.grow(20), this.c2);
}
Because these examples are just testing a boolean, we can use assertTrue or assertFalse.
You then run this as a JUnit test.
What We Learned
Data:
- Classes vs interfaces
- Interfaces tell classes what they should do
- Represent behavior without implementation
- Makes programs more flexible Abstract Classes:
- Common behavior, common fields (prevents code duplication)
- Subclasses
- make it more specific
- Add behavior to a library class
- Special case of a super class
Linked lists, direct access, trees, maps
Generics
- Type parameters, abstract types
Efficiency and complexity:
- Differences in constants, n log(n), polynomial, exponential
Datatypes:
| Datatypes | Fundies 1 | Fundies 2 |
|---|---|---|
| Compound | structs |
classes |
| Lists | lists |
indexes, direct access, mutable |
| Trees | Trees | IAT, BST, Heaps |
| Graphs | Graphs | Cyclic |
| Maps | did not see | hashmaps |
Abstracting:
| Abstracting and Sharing Code | Fundies 1 | Fundies 2 |
|---|---|---|
| Over data | helper functions | helper methods |
| Over behavior | functions as arguments | function objects |
| Over behavior for union data | functions as arguments | visitors |
| Over types | did not see | generics |
Testing:
| Testing | Fundies 1 | Fundies 2 |
|---|---|---|
| Designing test cases | Yes | Yes |
| Testing for Correctness | Yes | Yes |
| Testing under mutation | No | Yes |
Working with mutation:
- Argue for termination
- Test properly - test fixtures
- Understand how data is passes around, it’s stored, saved
- Aliasing
Why OOD?
Designing software is not easy.
You will need to be able to deal with complexity and flexibility
Central concepts:
- Information hiding
- Interfaces
- Closed to modification, open to extension
Topics for OOD:
- What are objects all about?
- Interface polymorphism (interfaces don’t tell you what you need for the fields)
- Always use the more general type for implementation
Interface polymorphism
- It can be reassigned to other objects in the interface
IShape c1 = new Circle(...);
c1 = new Rectangle(...);
List<Integer>
// ArrayList
// LinkedList
// etc
Map<String, Integer>
// HashMap
// etc
- Data abstraction and encapsulation