CS1800 Discrete Structures
Module 2 - Statement Representation
Circuits and Logic
- OR
- ADD
- XOR
- XNOR
- NAND
Half Adder Circuit
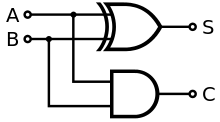
S Is the sum and c is the carry. Uses xnor for the sum because 0 xnor 0 = 0, 1 xnor 0 = 1, and 1 xnor 1 = 0 (where the carry is).
Ripple Adder
What if you want a third input? You have to expand the Half Adder
Boolean Algebra
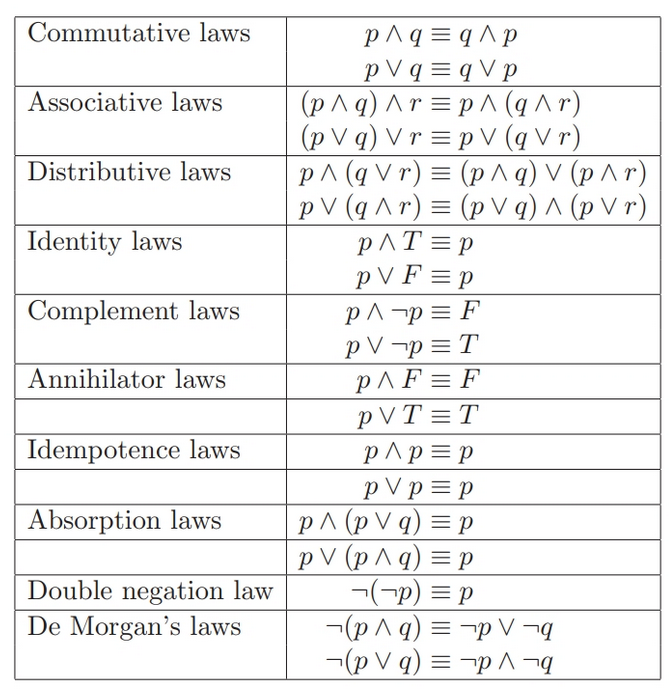

Boolean Equivalence
$(A \wedge \neg B) \vee (A \vee B) \equiv A$
Distributive Law: $((A \wedge \neg B) \vee A) \wedge ((A \wedge \neg B) \vee B)$
Commutative Law: $(A \vee (A \wedge \neg B)) \wedge ((A \vee B) \wedge (B \vee \neg B))$
Absorption Law and Known Always True: $A \wedge (A \vee B)$
Absorption: $A$
Implications, Inverses and Contrapositives
Conditionals/Implications
- If
pthenq
Example:
p: Ben left the house after 8am
q: Ben arrived at work after 9am
If Ben left after 8am, then Ben arrived after 9pm
$p \to q$ (we use double arrow notation $\implies$)
“If p then q”
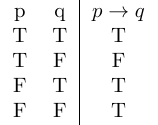
What if we flipped the truth table?

This proves that
\[\neg (p \to q) \equiv p \wedge \neg q\] \[p \implies q \equiv \neg(p \land \neg q) \equiv \neg p \lor q\]Contrapositives
$p \to q \equiv \neg q \to \neg p$
If Ben arrived before 9, he must’ve left before 8
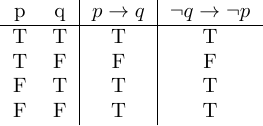
Converse of $p \to q$ is $q \to p$
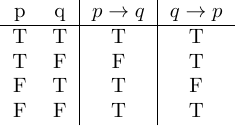
If Ben arrives after 9, then Ben left after 8
Inverse $\neg p \to \neg q$
(Contrapositive of the Converse)
Existential Qualifiers
Quantities
- None
- Some
- All
It rained every first day of the month last string (March, April, May)
On every first day of the month, it rained
On every x, it rained
$p(x)$= it rained on $x$ →on every $x$, $p(x)$
for all first days of the month, it rained
- For all $x$, it rained
- for all, $x$, $p(x)$
Denotated as:
\[\forall x, p(x)\]$x$ is the first day of the month
$x \in$ first days of the month
$\forall$ - Universial Quantifiers
- On every
- For all
- For every
- For each
- All of
Example
$Q(x)$ : $x$ has green leaves, $x$ is a tree
$\forall x, Q(x)$ : Every tree has green leaves
- NOT True
Some trees have red leaves → There is a tree with red leaves (only have to prove one)
$R(x)$ : $x$ has red leaves
\[\exists x, R(x)\]There exists a tree with red leaves
Example:
$\forall x, R(x)$ - All trees have red leaves
Negate: Exhibit a tree with leaves that aren’t real. Some trees don’t have red leaves
Therefore:
$\forall x, R(x)$
Negate: $\exists x, \neg R(x)$
Example: There are some trees that have purple leaves.
Every tree doesn’t have purple leaves
$\exists x, purple(x)$
Negate: $\forall x, \neg purple(x)$
Summary:
$\neg \forall x, p(x) \equiv \exists x, \neg p(x)$
$\neg \exists x, R(x) \to \forall x, \neg R(x)$
None: $\forall x \neg p(x)$
All : $\forall$
Some: $\exists$
Module 3 - Collection Representation
Lesson 1 - Set Representation
Set of locations that Northeastern has a campus in (each one of them is called an element):
- London
- Portland
- …
- Boston
NOTE: Sets cannot have duplicates
Notation
NU_CAMPUS = {London, Portland, …, Boston}
$\in$ - an element of
Ex. London $\in$ NU_CAMPUS
Infinite Sets
In order to represent infinite sets (ex. multiples of 5), we need to use set builder notation
Multiple of 5:
| { x | x = 5 * n, n ≤ 1} |
This example isn’t too clear because the ncan be any number like 1.3, not just natrual numbers.
Numbers
- Natrual - $\N$
- Integers - $\Z$
- Rationals - $\mathbb{Q}$
- Real - $\R$
Therefore the multiple of 5 example should look like this:
| { x | x = 5 * n, n $\in \N$} or { 5n | n $\in \N$} |
The first one is perferred because it represents computer programming languages
General Notation
| { x | the rules governing membership} |
Lesson 2: Subsets, The Empty Set and The Power Set
Recall:
NU_CAMPUS = {London, Portland, …, Boston}
NU_US_CAMPUSES = {Boston, Seattle, …}
Subsets - $\subseteq$
NU_US_CAMPUSES $\subseteq$ NU_CAMPUS
Another example: Fives = { x | x = 5 * n, n $\in \N$}
| Tens = { x | x = 10 * n, n $\in \N$} |
Tens $\subseteq$ Fives
General Notation
If and only if - $\iff$
Ex:
A $\subseteq$ B $\iff$ $\forall$ x $\in$ A, x $\in$ B
If not in a subset:
A $\nsubseteq$ B $\iff$$\exists$ x $\in$ A, x $\notin$ B
Proper Subset - $\subset$
C $\subset$ D $\iff$$\forall$ x $\in$ C, x $\in$ D and $\exists$ y $\in$ D, y $\in$ C
E $\subseteq$ F and F $\subseteq$ E $\iff$E $\equiv$ F (very helpful for proofs)
The Empty Set
- Represented with {} or $\emptyset$
- Is a subset of every other set
The Power Set
- The power set is a set of all possible subsets of any given set
Example:
IC = {chocolate, strawberry, vanilla}
$\wp (IC)$ = { {}, {chocolate, strawberry, vanilla}, {chocolate}, {strawberry}, {vanilla}, {chocolate, strawberry}, …}
Every set is a subset of itself
How many elements are in $\wp (IC)$?
- IC - 3 elements
- $\wp (IC)$ - 8 elements
Notice that $8 = 2^{3}$
We can make this into a general form:
- A - n elements
- $\wp (A)$ - $2^{n}$ elements
Lesson 3: Operations on Sets
- Complement of a set
- Union
- Intersection
- Difference
- Cartesian Product
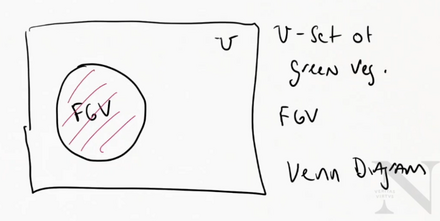
Favorite Green Vegetables (FGV) - there is an implied context. It is Ben’s favorite things in the universe green vegetables
Universe - $\mho$
FGV = {cucumber, peas, lettuce, broccoli}
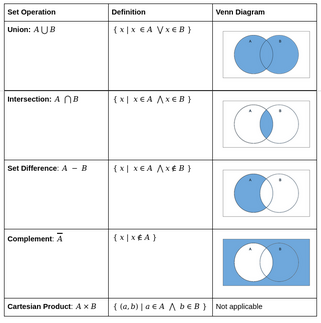
Venn Diagram Representations of Sets
Complement
Complement of FGV
- All green vegetables not in that set
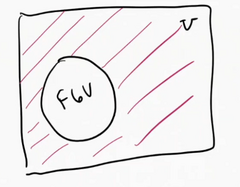
The complement of a set A, is written $\bar{A}$
$\bar{A}$ is the set of all elements in a universe that aren’t in A
| Formation Definition: $\bar{A} = {x | x \notin A, x \in \mho}$ |
NOTE: The $x \in \mho$ is optional and most often left out
FGV = {cucumber, peas, lettuce, broccoli}
MGV = {cucumber, lettuce, asparagus}
Union
Addition of sets
FGV $\cup$ MGV = {cucumber, lettuce, asparagus}
$A \cup B = B \cup A$
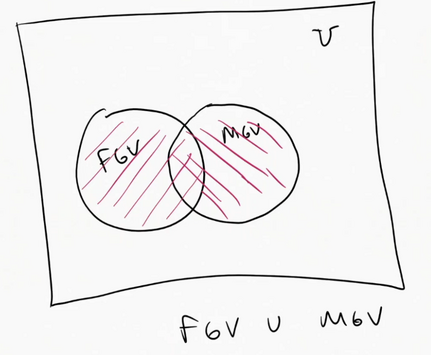
The union of a set A with a set B written, $A \cup B$, is th set of all elements in A and all elements in B
Formal Definition:
| $A \cup B = {x | x\in A \vee x \in B}$ |
Intersection
All of the elements in common
$FGV \cap MGV = {cucumber, lettuce}$
$A \cap B = B \cap A$
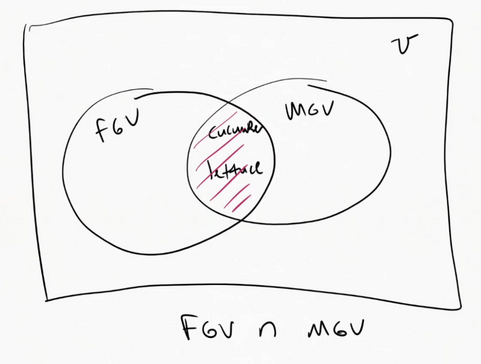
The intersection of a set A with a set B is the set of all elements that are in both A and B
Formal Definition:
| $A \cap B = {x | x \in A \wedge x \in B }$ |
Unions and intersections of more than two sets:
| $A \cup B \cup C = {x | x \in A \vee x \in B \vee x \in C }$ |
| $A \cap B \cap C = {x | x \in A \wedge x \in B \wedge x \in C }$ |
Formal Explanation:
$\bigcup\limits_{i=1}^{n} A_{i} = A_{1} \cup A_{2} \cup A_{3} … \cup A_{n}$
$\bigcap\limits_{i=1}^{n} A_{i} = A_{1} \cap A {2} \cap A{3} … \cap A_{n}$
Difference
What’s in one set and not the other
- Ordered operation! $\therefore A - B \neq B - A$
Recall:
FGV = {cucumber, peas, lettuce, broccoli}
MGV = {cucumber, lettuce, asparagus}
$FGV - MGV = { peas,brocolli}$
Sometimes it’s written $FGV / MGV$
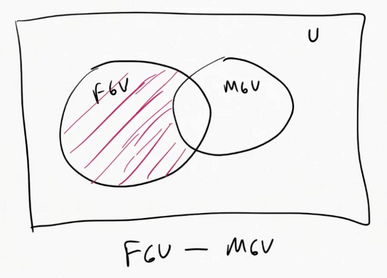
The difference between set A and B, written $A-B$, is the set of all elements in A that not in B
Formal Definition:
| $A - B = {x | x\in A \wedge x \notin B }$ |
Cartesian Product
All possible pairs
Recall the Cartesian plane which represents all possible pairs of x and y positions
$GV = {cucumber, peas}$
$berry = {blue, straw, black }$
$GV \times berry = {(cucumber, blue), (cucumber, straw), (cucumber, black), (peas, blue), (peas, straw), (peas, black)}$
Parenthesis mean pair
Definition:
The Cartesian product of set A with set B, written $A \times B$, is the set of all possible pairs from A with the elements in B.
| $A \times B = {(x,y) | x \in A \wedge y \in B}$ |
This is useful for pairing things in databases
Symmetric Difference
Everything but the intersection
$A \vartriangle B = (A - B) \cup (B -A)$
Lesson 5 - Binary Strings
Consider the universe:
$u = [vegtables, fruits, grains, protein, dairy]$
Length 5
If we have the set:
$s = {vegtables, protein}$
This set corresponds to the 1st and 4th elements in the given universe so we can denote it as:
$10010$
It’s 5 bits because the universe is length 5. Notice how only the 1st and 4th digit (from the left) is 1.
Lesson 6 - Writing Proofs
Proof - A mathematical reason that something is true
- Arguing something
Prove that $A - B \equiv A \cap \bar{B}$
Belief Phase
- Use the Venn diagrams to convince yourself that the statement is true
Explain the statements to their formal definitions:
| $A - B = {x | x \in A \wedge x \notin B }$ |
| $A \cap \bar{B} = {y | y \in A \wedge y \in \bar{B}}$ |
They already look very similar
Prove Idea
A rough skeleton of the formal proof. This is called a direct proof.
- How do we show set equivalence?
Set Equivalence Laws
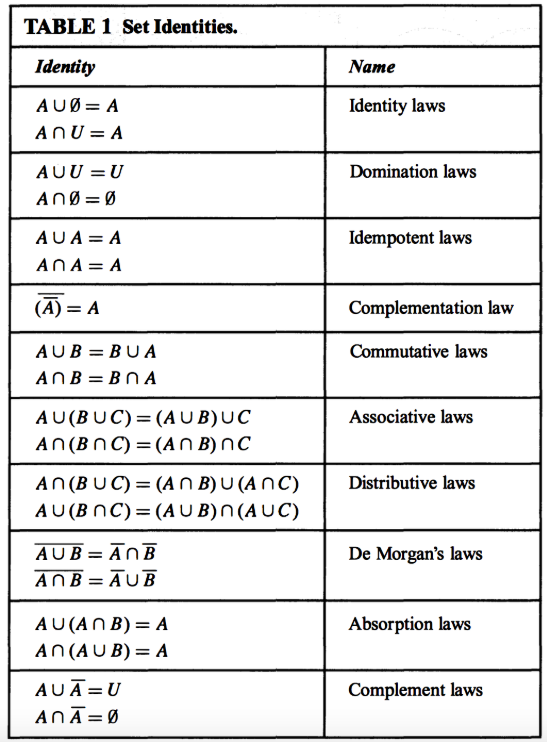
In order to prove this, we need to first prove this:
$A - B \subseteq A \cap \bar{B}$ and
$A \cap \bar{B} \subseteq A - B$
$x \in A - B \implies x \in A \wedge x \notin B \implies x \in A \wedge x \in \bar{B}$
$x \in A \cap \bar{B} \implies x \in A \wedge x \in \bar{B} \implies x \in A \wedge x \notin B$
The Actual Proof
THM: A - B \equiv A \cap \bar{B}
Proof:
To show that the set A - B is equivalent to the set A \cap \bar{B} we will
show that A - B \subseteq A \cap \bar{B} and A \cap \bar{B} \subseteq A - B.
First we will show A - B \subseteq A \cap \bar{B}. Consider the definition
of A - B, A - B = \{x|x \in A \wedge x \notin B \} since x \in A \wedge x \notin
B, we know htat x \in A \wedge x \in \bar{B} by the definition of set complement
so x \in A \cap \bar{B}. Now to show A \cap \bar{B} \subseteq A - B we again
consider the definition A \cap \bar{B} which is the set of all x, x \in A
\wedge x \in \cap{B} but since x \in \bar{B} is the same as x \notin B by
definition, we know x \in A \wege x \notin B which is the same as x \in A - B.
So when x \in A \cap \bar{B} \implies x \in A - B. So we have A - B \subseteq A
\wedge \bar{B} and A \wedge \bar{B} \subseteq A - B so A - B \equiv A \wedge
\bar{B}. \boxtimes
You end formal proofs with either $\boxtimes$ or $Q.E.D$
Summary
2346
Sets
Sets are collections of unique objects, meaning there are no duplicates. We can write them either in list notation or set builder notation.
$S = {0,1,2,3}$
$x \in A$: x in an element of A
$A \equiv B$: A is equivalent to B if both sets have the exact same elements
$A \subseteq B$: A is a subset of B if all elements in A are also in B.
$A \subset B$: A is a proper subset of B if A is a subset of B but A is not equivalent to B.
Special Sets
We learned of a number of special sets.
$\empty$ is the empty set, written as ${}$in list notation. Note that for all sets A, $\empty \subseteq A$.
$\mathcal{P}(S)$ is the power set of S, or all subsets of S.
$\mathbb{Z}$ is the set of all integers
$\mathbb{Q}$ is the set of rationals, or all fractions.
$\mathbb{R}$ is the set of reals, which are rationals and all irrational numbers like $\pi$.
$U$ is the universe and contains all objects.
Set Operations
Just like boolean statements, we can create new sets using set operations. We can also visualize these sets with Venn Diagrams.
Proving Equivalence of Sets
We can prove two sets A, B are equivalent using the set equivalence laws or by proving A, B are subsets of each other.
Recall $A \equiv B \iff A \subseteq B \land B \subseteq A$
By definition of AB, we can show ABby showing for all objects x, if xA, then xB. So our proofs look as follows:
- Announce we will prove $A \equiv B$ by showing $A \subseteq B$ and $B \subseteq A$.
- Show $A \subseteq B$ by showing if $x \in A$, then $x \in B$
- Then show $B \subseteq A$ by showing if $x \in B$ then $x \in A$.
- Conclude we have indeed shown $A \equiv B$.
Module 4 - Set Cardinality
Lesson 1 - Counting Unions
Counting Sets
$nucampus = {London, Portland, Boston}$
| Set cardinality - $ | nucampus | $ |
- The number of elements
GV = {cucumber, kale, asparagus, peas}
Berries = {Black, straw, raspberry, blue berry}
| $ | GV \cup Berries | $= | {cucumber, kale, asparagus, peas, black, straw, rasp, blue} = 8 |
| $ | GV \cup B | = | GV | + | B | $ |
- Is this always true? NO!
- It’s not if you have overlap, because you would count the overlap twice
Remove duplicates:
Inclusion/Exclusion Principle
2 Sets General Form:
| $ | A \cup B | = | A | + | B | - | A \cap B | $ |
What about for 3 sets?
- You have to once more get rid of the overlap (which could be counted an additional time than with 2 sets)
3 Sets General Form:
| $ | A \cup B \cup C | = | A | + | B | + | C | - | A \cap B | - | A \cap C | - | B \cap C | + | A \cap B \cap C | $ |
- You need to add the shared elements of all 3 again (you cut it out too many times)
4 Sets General Form:
| $ | A \cup B \cup C \cup D | = | A | + | B | + | C | + | D | - | A \cap B | - | A \cap C | - | B \cap D | - | C \cap D | + | A \cap B \cap C | + | A \cap B \cap D | + | A \cap C \cap D | + | B \cap C \cap D | - | A \cap B \cap C \cap D | $ |
Lesson 2: Counting Cartesian Products
WestCoast = {Vancoover, Seattle, San Fran, Fan Jose}
EastCoast = {Portland, Charlotte, Boston}
LT = {London, Toronto}
Need one person from each region
FwC = {Bethany, Ian, Jodi}
FeC = {Lany, Maria}
FLT = {Nate, Paul, Samantha}
1 Person to join from each region
How Many Different Combinations?
FwC x FeC x FLT = {(Bethany, Laney, Nate), (Bethany, Maria, Nate)…}
Let’s visualize this in a tree:
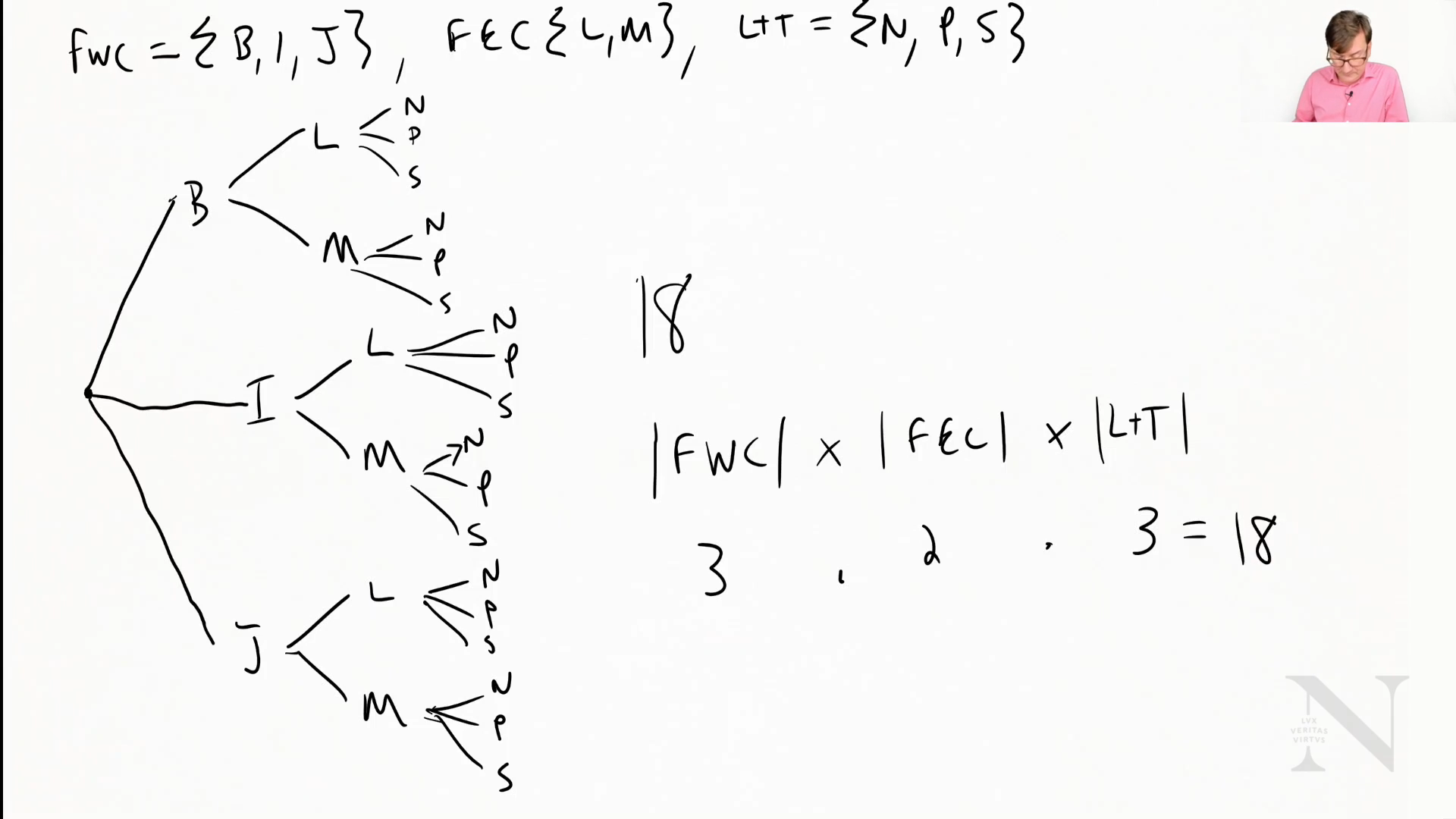
How Many Possible 4 Digit Pin Numbers Are There?
Because we multiply how choices we have by the amount of the times we have to make a choice, we get
| Digits = {0,1,2,3,4,5,6,7,8,9} $\therefore$ | Digits | = 10 |
10 * 10 * 10 * 10
Lesson 3: Pigeonhole Principle
Example 1:
7 Teams that are going to have students assigned to
8 Students in the class
What can I say happens when I assign students to a team?
No matter what, one team has at least 2 students
Example 2:
7 Teams
22 Students
No matter the placement/assignment, if all students are on some team then there is 1 team that has at least 4 students
Example 3:
25 Professors
6 TAs
Rule:
- Every professor has exactly 1 TA
What can I say about the number of professors per TA?
Then 1 TA is assigned to 5 professors
Pigeon Hole Principle - General Definition
If you have k+1 objects in k bins, at least one bin has more than 1 object
General Formula
If you have n objects to pack into k bins, then at least one bin has at least $\lceil \frac{n}{k} \rceil$ objects
- $\lceil n \rceil$ is a ceiling which means that you round up
- $\lfloor n \rfloor$ is a floor which means that you round down
Example:
25 professors
6 TAs
Every professor has exactly 1 TA
One TA with $\frac{25}{6} = 4 \frac{1}{6}$
$\therefore$ one TA has at least 5 professors if every professor has 1 TA
Example 2:
25 professors
6 TA’s
Rules:
- Every professor has a TA
- No TA has more than 5 professors
At least 3 TA’s are assigned to 4 or more professors
WHY?
If we have 25 professors that need to be assigned to 6 TAs and every professor must be assigned to TA AND no TA is assigned to more than 5 professors then at least 3 TA’s are assigned to 4 or more professors.
A - 25 professors are assigned 6 TA’s and each professor has 1 TA and no TA has more than 5 professors
B - At least 3 TA’s are assigned to 4 or more professors
$A \implies B$
Negation : $A \land \neg B$
Proof By Contradiction
Proof by contradiction. Assume not, we have 25 professors assigned to 6 TAs such that every professor is assigned to exactly one TA and no TA has more than 5 professors. We also have by our assumption that fewer than 3 TA’s have 4 or more professors. Then we have at most 2 TAs with 4 or more professors. Consider the case when 2 are assigned 4 and all others are smaller. Then we have 17 professors to assign to 4 TA’s. By the pigeonhole principle we know at least 1 has $\lceil \frac{17}{4}\rceil = \lceil4.25 \rceil = 5$ leaving at least 3 with more than 4. Causing a contradiction $\Rightarrow \Leftarrow$
Module 5 - Combinatorics and Permutations
Summary
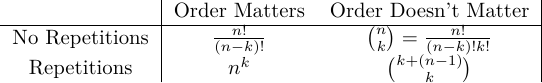
Recitation Notes
Lesson 1: Permutations (order matters and no repetitions)
How many ways can we order n objects?
A = {a,b,c}
Ex.
- abc
- acb
- bac
- bca
- cba
- cab
6 Ways!
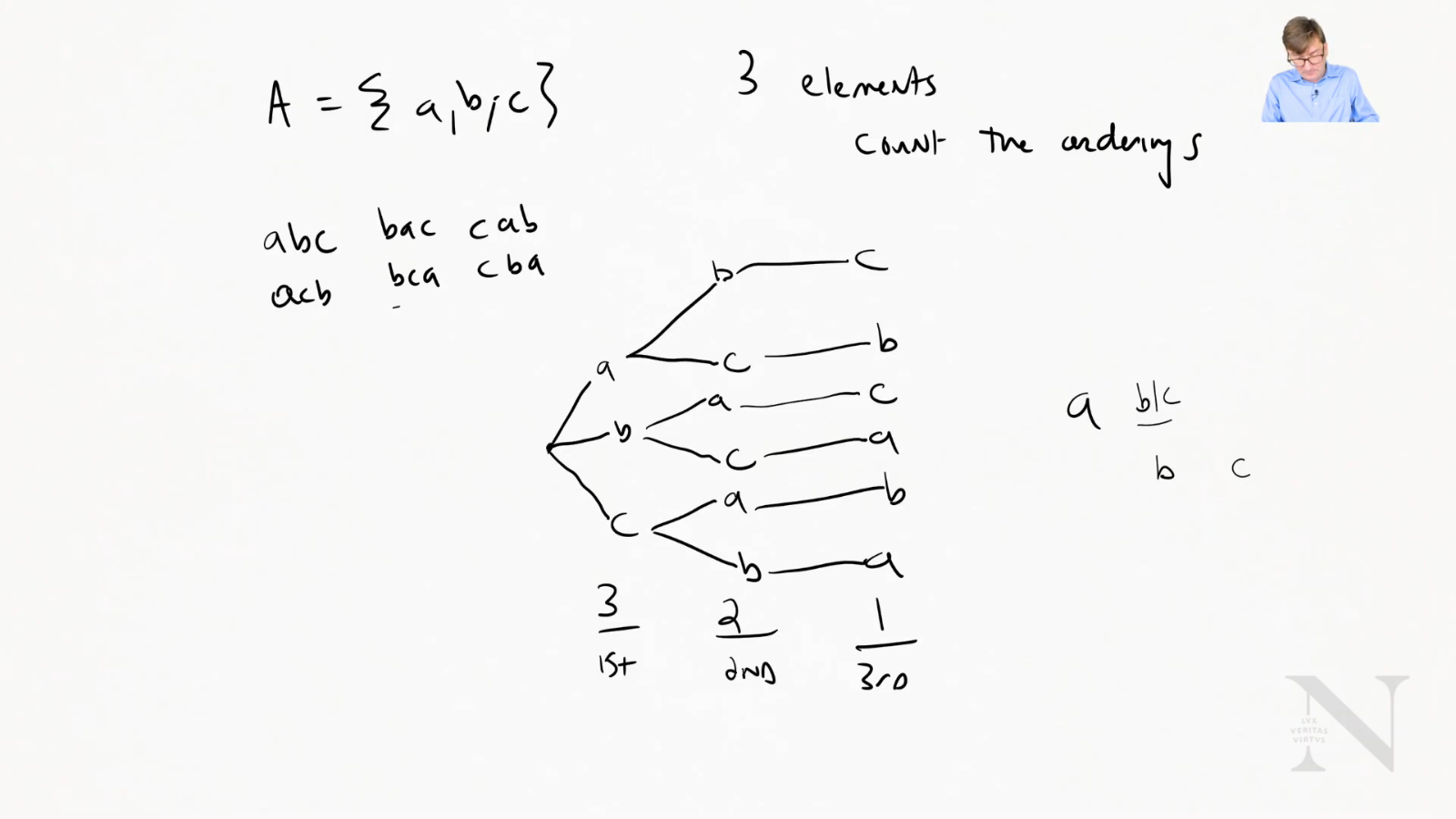
General Formula
3 elements - 321
4 elements - 432*1
$\therefore n!$
Sidenote: $\sum$ for multiplication is $\prod$ therefore $n! =\prod_{i=n}^{1} i$
Example
How can we choose k elements from a set of n when order matters?
D = {0,1,2,3,4,5,6,7,8,9}
| D | = 10 |
Pick 4 elements
- Order matters
- No repetition
1st choice : 10 possibilities
2nd choice : 9 possibilities
3rd choice : 8 possibilities
4 choice : 7 possibilities
1098*7
Remember: We stopped at k, so it’s no entire factorial. We need to cut off the rest of it
$\frac{n!}{(n-k)!}$ or $p(n,k)$
Lesson 2: Combinations (Order doesn’t matter and no repetition)
No repetitions
- The default with sets! Assume this!
ex. Choose 2 elements from a set of 4
A = {a,b,c,d}
Recall: order matters would be $\frac{4!}{(4-2)!} = 12$
However $ab=ba$. In this example, that would mean that we cut the options in half
Written as ${4}\choose{2}$ or $c(4,2)$
- Pronounced “4 choose 2”
General Definition:
${n}\choose{k}$$= \frac{n!}{(n-k)!k!}$
k! is added because we overshot by how many times we can order k elements
Examples
Let’s consider we have 9 people, we want to know the number of possible teams we can make of size 5.
${9}\choose{5}$$= \frac{9!}{(9-5)!5!}$
Variant:
9 people, teams of size 5. But 2 people, Logan and Andrew must together if picked.
Two cases
- Logan and Andrew are picked
- ${7 \choose 3}$
- No Logan + No Andrew
- ${7 \choose 5}$
${7 \choose 3} + {7 \choose 5} =$
Variant:
9 people, need team of 5, but Ben can’t work with Nate.
3 Cases
- Ben is on + Nate is out
- ${7 \choose 4}$
- Nate is on + Ben is out
- ${7 \choose 4}$
- Ben is out + Nate is out
- ${7 \choose 5}$
${7 \choose 4} + {7 \choose 4} + {7 \choose 5} =$
Logical Evaluation:
$\neg Ben \lor \neg Nate$
Negate: $Ben \land Nate$
Things that can’t happen:
- Both Ben and Nate are on
- ${7 \choose 3}$
Difference Method
${9 \choose 5} - {7 \choose 3} = 91$
Teams with Types
12 People
- 5 Faculty
- 7 Students
Teams of size 5
How many teams have 3 faculty members and 2 students?
${5 \choose 3} \cdot {7 \choose 2} = 210$
How many teams of size 5 contain at most 1 faculty?
2 Cases
- 0 faculty + 5 students
- ${7 \choose 5} \cdot {5 \choose 0}$
- 1 faculty + 4 students
- ${7 \choose 4} \cdot {5 \choose 1}$
${7 \choose 5} \cdot {5 \choose 0} + {7 \choose 4} \cdot {5 \choose 1}$
How many teams have at least 1 faculty members?
5 cases
- 1 fac + 4 students
- ${5 \choose 1} \cdot {7 \choose 4}$
- 2 fac + 3 students
- ${5 \choose 2} \cdot {7 \choose 3}$
- 3 fac + 2 students
- ${5 \choose 3} \cdot {7 \choose 2}$
- 4 fac + 1 student
- ${5 \choose 4} \cdot {7 \choose 1}$
- 5 fac + 0 students
- ${5 \choose 5} \cdot {7 \choose 0}$
${5 \choose 1} \cdot {7 \choose 4} + {5 \choose 2} \cdot {7 \choose 3} + {5 \choose 3} \cdot {7 \choose 2} + {5 \choose 4} \cdot {7 \choose 1} + {5 \choose 5} \cdot {7 \choose 0}$
Lesson 3: Counting with Repetitions when Order Matters
ex. 4 Digit pin
Digits = {0,1,2,3,4,5,6,7,8,9}
1st choice - 10 options
2st choice - 10 options
3st choice - 10 options
4st choice - 10 options
101010*10
$n^k$
Lesson 4: Balls and Bins: Counting With Repetitions When Order Doesn’t Matter
ex. Ordering pizza
4 pizza choices
- Cheese
- Pepperoni
- Veggie
- Meat Lovers
How many ways from this set can I get 3 pizzas?
- Create ‘bins’ with dividers
-
ex P C M V (‘1’ denotes a divider) - If you have a ‘ball’ in a bin, denote it with a 0 and the dividers are 1’s
- ex. 2 pepperonis, 1 cheese = 001011 (looks like binary)
- With 4 categories, you need 3 bars (which means 3 1’s)
- 3 pizzas to pick (which means 3 0’s)
How many binary numbers have 3 0’s and 3 1’s (6 bit)
- 6 bits long and you need to pick a location for the 3 1’s
- ${6 \choose 3}$
ex 2. 10 pizzas, 4 types
- 13 bits
- 3 ‘bars’ (1’s)
- 10 items (0’s)
${13 \choose 3}$
Or we could also ask where the 10 0’s are which would be
${13 \choose 10}$ (it’s the same answer)
General Formula
n - categories (n-1 1’s)
k - things to pick (k 0’s)
$(k+(n-1)) \choose k$

Module 6 - Probability
Summary

Lesson 1: Overview of Probability
Represents uncertainty
- Makes guesses
Lesson 2 Part 1: Events, Experiments, Sample Space and Probabilities
An event is something that might happen
- ex. flipping heads
An experiment or observation is a situation with one or more possible outcomes
- ex. flipping a coin (2 outcomes)
A probability is a real number in the range [0,1] (inclusive)
- 0 - Will not happen
- 0.5 - 50/50 chance
- 1 - Guaranteed to happen
$Pr(A)$ - Probability of A
$Pr(heads) = 0.5$ or $Pr(C=H) =0.5$
- Where C is a random variable and H is what we’re interested in
Dice Example
S = {1,2,3,4,5,6}
| $Pr(event) = \frac{ | E | }{ | S | }$ |
Either 5 or 6:
E = {5,6}
$Pr(\text{roll 5 or 6}) = \frac{1}{3}$
Coin Example
S = {H,T}
E = {E}
$Pr(heads)=0.5$
Two Dice Example
S = {(1,1),(1,2)….,(6,6)}
| $ | S | = 6\times6= 36$ |
What is $pr(\text{doubles})$?
E = {(1,1), (2,2) …}
| $Pr(\text{doubles}) = \frac{ | E | }{ | S | } = \frac{1}{6}$ |
Sum to 6:
E = {(1,5), (2,4) …}
$Pr(\text{roll a 6}) = \frac{5}{36}$
Flipping 4 Coins
| $ | S | = 2^{4} = 16$ |
Example: Exactly 2 heads
| $ | E | = {4 \choose 2} = 6$ |
- We can use our combinations knowledge here
$Pr(\text{2 heads}) = \frac{3}{8}$
Lesson 2 Part 2: Fallacies to Avoid
- Two outcomes does NOT mean equal chance
Inclusion-Exclusion Principle
$Pr(E_{1} \cup E_{2}) = Pr[E_1] + Pr[E_2] - Pr[E_1 \cap E_2]$
Lesson 2 Part 3: Sampling with and Without Replacement
- Without replacement
- Cannot draw an item again
- With replacement
- Can draw an item again
Example: Urns and balls
20 balls
- 18 are red
- 2 are green
With Replacement
S = {red1, red2, green1…}
Valid Draw: {r1,r1,g1}
Draw 2 Balls:
| $ | S | \times | S | \times | S | = 20\times 20\times 20 = 8,000$ |
$Pr(\text{0 green balls}) = \frac{18^3}{8,000} = 0.729$
$Pr(\text{3 green balls}) = \frac{2^3}{8,000} = 0.001$
Without Replacement
Valid Draw: {r1,r2,g1}
Sample Size Space: $C(20,3) = 1140$ ←Outcomes
$Pr(\text{0 green}) = \frac{C(18,3)}{1,140} = 0.716$
Axons of Probability
- Range [0,1]
- $Pr(A) + Pr(\neg A) = 1$ (union of events)
- $Pr(A\cup B) = Pr(A) + P(B) - P(A\cap B)$
Lesson 3: Independence and Conditional Probability
Events are independent if and only if $Pr(A\land B) = Pr(A) \times Pr(B)$
Example: At least one double in 3 rolls → Independence
$1-Pr(\text{no doubles on 3 rolls})$
Example:
| $Pr(\text{sum of die1 and die2 is 7 | die1 is 6})$ |
-
NOTE: means “given”
When die1 is a 6: {(6,1),(6,2)…}
- 6 outcomes
When sum is 7 and die1 is a 6: {(6,1)}
- 1 outcome
| $Pr(\text{die1 + die2 = 7 | die is a 6}) = \frac{1}{6}$ |
General Formulas - Dependence
| $Pr(A | B) = \frac{Pr(A\land B)}{Pr(B)}$ |
| $Pr(A | B) = \frac{ | (A\cap B) | }{ | B | }$ (holds by definition) |
General Formulas - Independence
If and only if A and B are dependent: $Pr(A\land B) = Pr(A) \times P(B)$
| Independence holds if and only if $P(A | B) = Pr(A)$ |
Example: Critical Bugs in Code
$Pr(\text{Bugs}) = Pr (\text{Bugs}\land\text{SB}) + Pr(\text{Bugs}\land\neg\text{SB})$
| $= Pr(\text{Bugs} | \text{SB})\times Pr(\text{SB}) + Pr(\text{Bugs} | \neg\text{SB}) \times Pr(\neg\text{SB})$ |
= 0.12
Lesson 4 Part 1: Mathematical Expectation
Expected Value
- Value you should get if you average over many trials
The expectation of a random variable (r.v.) X is $E[X] = \sum_x Pr(X=x) \times x$
Example:
D = outcome of a 6-sided die
$E[D] = \frac{1}{6}\times 1 + \frac{1}{6} \times 2 + \frac{1}{6} + 3 … \frac{1}{6} \times 6 = 3.5$
Example:
L = outcome of the lottery with 1 in 10 million chance of winning, $2 million payout
$E[L] = 2,000,000 (\frac{1}{10,000,000}) + 0\times\frac{9,999,999}{10,000,000} = $0.20$
Linearity of Expectation
Given rv (random variables) x, y and z=x+y then
$E[z] = E[x]+E[y]$
Example: Let z = sum of 2 six-sided dice. Let x and y be the first and 2nd rolls
$E[z] = E[x] + E[y] = 3.5 + 3.5 = 7$
Look out for this in exams!
Lesson 5: Bayes’ Rule
How to combine:
- Prior degree of belief
-
Evidence
- A model of how likely it is that each hypothesis would produce the available evidence
| $Pr(\text{hypothesis | evidence}) \propto Pr(\text{hypothesis}) \times Pr(\text{evidence | hypothesis})$ |
More precise:
| $Pr(\text{hypothesis | evidence}) = \frac{Pr(\text{hypothesis}) \times Pr(\text{evidence | hypothesis})}{Pr(\text{evidence})}$ |
- We, however, don’t need to precise answer when comparing two probabilities
General Formula
| $Pr(\text{A | B}) = \frac{Pr(A) \times Pr(B | A)}{Pr(B)}$ |
Bayes’ Rule follows from the definition conditional probability
Derivation
| $Pr(A\land B) = Pr(A | B) \times Pr(B) = Pr(B | A) \times Pr(A)$ |
| $Pr(A | B) = \frac{Pr(B | A) \times Pr(A)}{Pr(B)}$ |
Example: If I have a bag with 6-sided die and 20-sided die and I pull one out at random and roll a 6. Is it more likely to be a 6 or 20 sided die?
| $Pr(\text{6 | 6-sided-die}) = \frac{1}{6}$ |
| $Pr(\text{6 | 20-sided-die}) = \frac{1}{20}$ |
| $Pr(\text{6-sided-die | 6}) \propto Pr(\text{6 | 6-sided}) \times Pr(\text{6-sided}) = \frac{1}{12}$ |
| $Pr(\text{20-sided-die | 6}) \propto Pr(\text{6 | 20-sided}) \times Pr(\text{20-sided}) = \frac{1}{40}$ |
It is more likely for it to be a 6-sided die
Modify the prior:
- Bag contains 4 20-sided and 2 6-sided
$Pr(\text{6-sided}) = \frac{1}{3}$
$Pr(\text{20-sided}) = \frac{2}{3}$
| $Pr(\text{6-sided-die | 6}) \propto Pr(\text{6 | 6-sided}) \times Pr(\text{6-sided}) = \frac{1}{18}$ |
| $Pr(\text{20-sided-die | 6}) \propto Pr(\text{6 | 20-sided}) \times Pr(\text{20-sided}) = \frac{1}{30}$ |
Still more likely for it to be a 6-sided die
Lesson 6: Variance
Variance: How spread out a distribution is. How far are the samples to the mean on average?
$E[x-E[x]] = 0$ (because the negatives and positives negate each other by definition)
Definition: For a r.v. X, $var(x) = E[(x-E[x]^2)]$ or $var(x) = E[x^2] - E[x]^2$
The standard deviation of x is $\sqrt{var(x)}$
Module 7 - Sequences, Series, and Induction
Lesson 1: Sequences
Order matters
ex. 3, 10, 17, 24, 31, 38
- Each element is called a term
Notation
- Counting starts at 1
- $a_1 = \text{1st term} =3$
- $a_2 = \text{2nd term} =10$
- etc.
Sequence
- A function between a subset natural numbers to a set of numbers
- 3, 10, 17, 24, 31, 38, … (the … means that it goes on forever)
- Notice in this example, there is 7 between each number
Arithmetic Sequence
- Grows by a fixed amount
Getting an Arbitrary Term:
ex. 3, 10, 17, 24, 31, 38, …
- Start at 3 and add 7 (x-1) times
- 3 + 7 (x-1)
- ex. get the 23rd term: 3 + (23-1) * 7
General Form:
$t(n) = a_1 + (n-1)d$
- $a_1$ is the starting term
- $d$ is the growth factor
Geometric Sequence
1, 5, 25, 125, 625, 3125, …
- You multiply by 5 each time
$t(n) = 1 \times5^{n-1}$
General Form:
$t(n) = a_1\times r^{n-1}$
- $a_1$ is the first term
- $r$ is the multiplicative factor
Quadratic Sequence
ex. 13, 23, 37, 55, 77
- 23-13 = 10
- 37-23 = 14
- 55-37 = 18
- 77-55 = 22
But what if we look at the differences as a sequence?
10, 14, 18, 22, …
- Has a growth factor of 4
In this case, 4 would be the second difference
Quadratic Sequence: **when the 2nd difference is a constant
General Form:
$t(n) = an^{2} + bn + c$
- Recall: this is the quadratic formula
ex. 13, 23, 37, 55, 77
What is the nth term for this?
$t(1) = 13 = a+b+c$
$t(2) = 23 = a*2^{2} + 2b + c = 4a+2b+c$
$t(3) = 37 = a3^2 + b3 +c = 9a+3b+c$
System of Linear Equations
-
System of Linear Equations
13, 23, 37, 55, 77
a+b+c = 13
4a + 2b + c = 23
9a + 3b + c = 37
9a + 3b + c = 37 + -4a - 2b - c = -23— ————————
5a + b = 14 4a + 2b + c = 23 + -a - b - c = -13— ————————
3a + b = 10 5a + b = 14 + -3a - b = -10— —————-
a = 2
Plug in values and you get:
$t(n) = 2n^2 + 4n +7$
Lesson 2: Series
Summing up terms:
$\sum_{i=1}^{5} a_i$ ←Sum up the first 5 terms
General Form:
$\sum_{i=1}^{n} a_i$
Ex.
1+2+3+4+5 = s
- 5+4+3+2+1 = s
— ———————
6+6+6+6+6 = 2s
General Form: Arithmetic Series
$\sum_{i=1}^{n} a_i = \frac{(n+1)n}{2}$
$\sum_{i=1}^{n} a_i = \frac{(a+(a+(n-1)d))n}{2}$
General Form: Geometric Series
Example: $3+\frac{3}{2}+\frac{3}{4}+\frac{3}{8}$
- r = $\frac{1}{2}$
- $n_1 = 3$
$\frac{s}{2} = \frac{3}{2} + \frac{3}{4} + \frac{3}{8} + \frac{3}{16}$
- If you subtract this by $3+\frac{3}{2} + \frac{3}{4} + \frac{3}{8}$ , it results in just the first and last term
$s-r*s = 1-r^n$
$s(1-r) = 1-r^n$
$\therefore s = \frac{a-r^n}{ar}$
Lesson 3: Proof By Induction
Example:
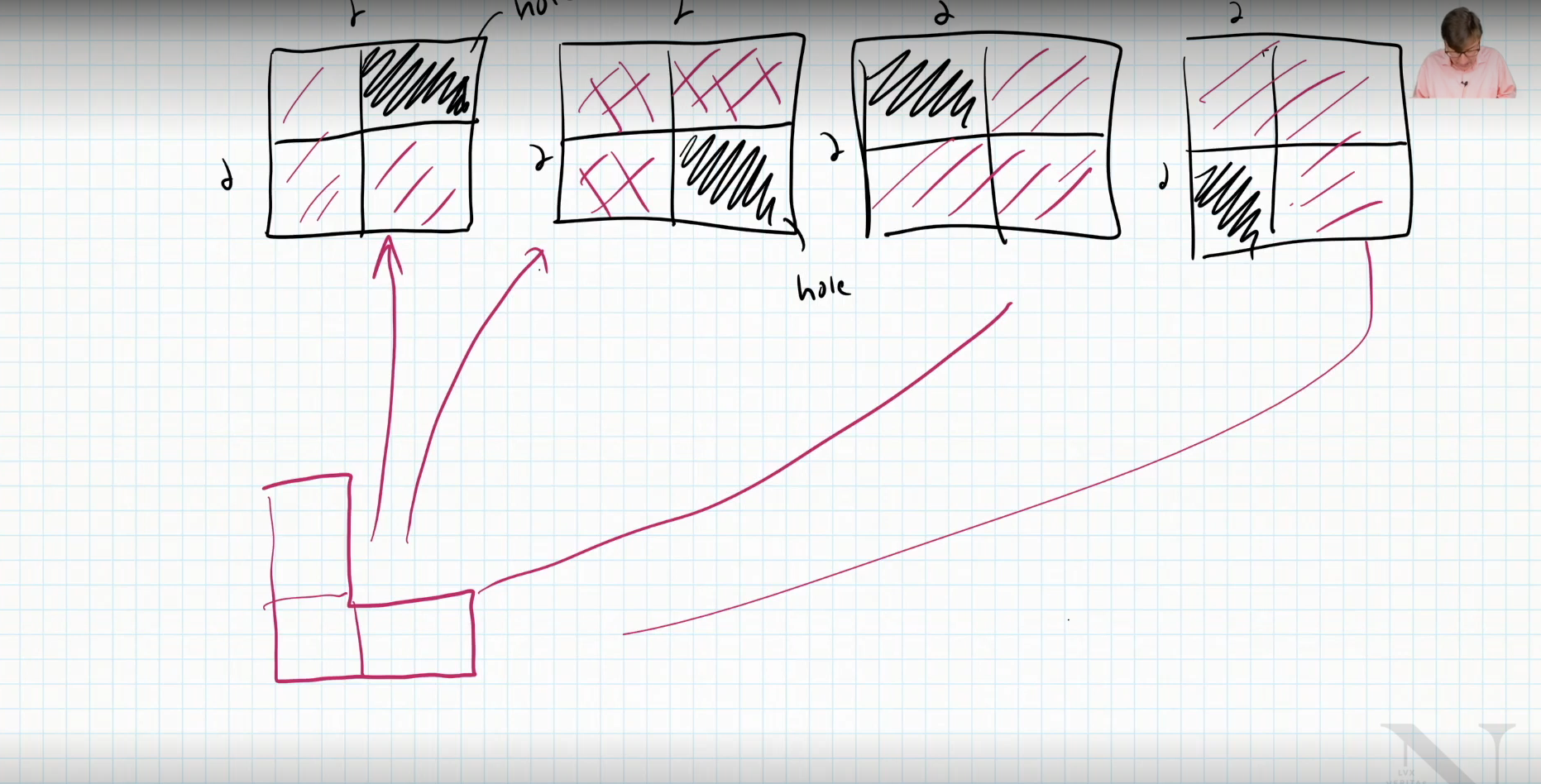
We proves that we can fit the L shaped piece into any 2x2 grid
What about 4x4?
- Yes, because we can split it up into 4 2x2 grids
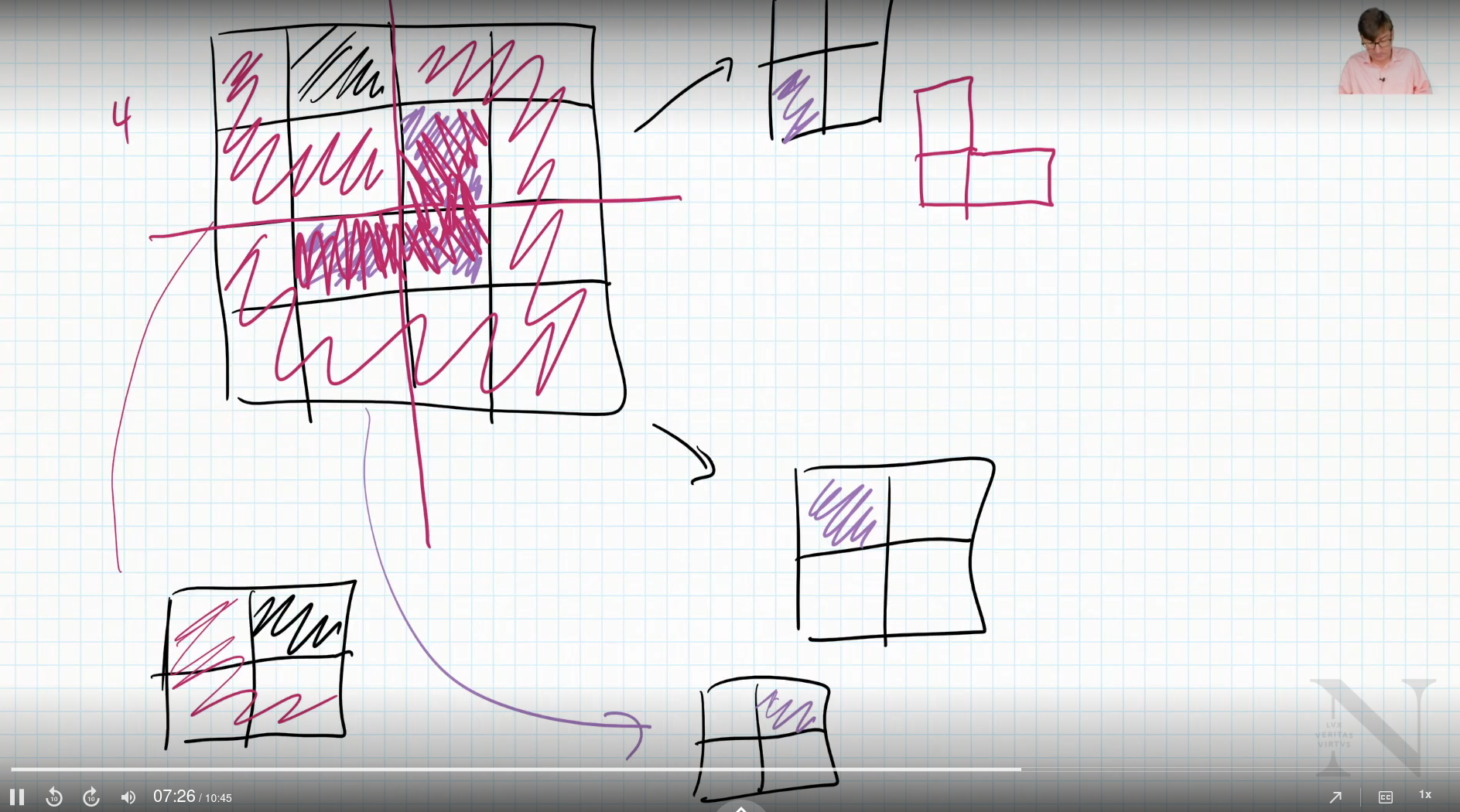
What about 8x8?
- Yes, because we can divide it into 4 4x4 grids
We are essentially building up a foundation
Example 2:
3 cent coin
5 cent coin
- Can we make any amount of change greater or equal to 8 cents?
Assume we have figured out how to make k cents worth of change using 3 cent and 5 cent coins. Can we make k+1 cents?
Case 1:
- No 5 cent coins
- In this case, take 3 3 cent coins away and add 5 cents
- k→k+1
Case 2:
- At least 1 5 cent coin
- In this case, remove 5 cent coin and add 2 3 cent coins
- k→ k+1
Proof by induction
Definition:
$P$ is some property defined over the integers and $a$ is some fixed integer and
- $P(a)$ is true (base case)
- $\forall k\in \mathbb{Z}, n \leq a, P(N)$ (inductive step)
This applies $\forall n \in \mathbb{Z} , n \geq a, P(n)$
Example:
- $P(n)$ - n cents can be made with 3 cent coins and 5 cent coins, $n\geq 8$
Proof by Induction
Consider the base case when n=8, we know that 8 can be made with 1 3 cent coin and 1 5 cent coin. Now consider the inductive hypothesis for an arbitrary k, k≥8. We can make k cents using 3 cent and 5 cent coins. Consider two cases. Case 1 in our k cents. The number of 5 cent coins is zero. Then remove 3 3 cent coins to make k-9 cents. Now add 2 5 cent coins to make k+1 coins. Case 2. We have at least 1 5 cent coin. Remove it to make k-5 cents. Now add two 3 cent coins to make k+1 cents. Since we know P(8) to be true and P(k) implies P(K+1) then P(n) is true for all $n\in \mathbb{Z}, n\geq 8$. Q.E.D.
Example:
$\sum_{i=1}^{n} i = 1+2+3…+n = \frac{n(n+1)}{n}$
Prove this by induction
- Base case
- Inductive step
Proof by Induction
Consider the base case when n=1 then we know $\frac{1(1+1)}{1} = 1$ which is the series with one term. Let’s assume for some $k$ $1+2+3…k = \frac{k(k+1)}{2}$ by our inductive hypothesis. Consider $1+2+3 …+k+(k+1)$which is $\frac{k(k+1)}{2} + (k+1)$ by our inductive hypothesis.
$\frac{k(k+1)}{2} = \frac{(k+2)(k+1)}{2}$
So we have $1+2+3…+k+(k+1) = \frac{(k+2)(k+1)}{2}$ as desired. So it is true for all n. Q.E.D.
Lesson 4: Strong Induction
Strong Mathematical Induction
$P(n)$ property defined over the integers with a, b fixed integers, a≤b. Base P(a), P(a+1), P(a+2), … P(b) are all true. Inductive $\forall k \geq b$ if P(i) is true $\forall i, a\leq i\leq k$ then P(k+1) is true. This implies $\forall n, n\geq a, P(n)$ is true.
Consider the Sequence:
$a_0 = 0,\ a_1=4,\ a_k = 6 \times a_{k-1} - 5 \times a_{k-2}$
$\therefore a_{2} = 6\times 4 - 5 \times 0 = 24$
$a_3 = 6\times 24 - 5 \times 4 = 124$
Claim $a_n = 5^n - 1$
- This needs strong induction
$P(n) = a_k = 6\times a_{k-1} - 5 \times a_{k-2}$
$a_n = 5^n -1$
Proof by Strong Induction
Consider the base case $P(0),\ P(1),\ P(2)$
$P(0) = a_0=0=5^0 -1 = 1-1 =0$
$P(1) = 4 = 5^1-1$
$P(2) = 24 = 5^2 - 1$
Consider the case when n is 0, we know that $5^0-1 = 0$, which is $a_0$ as defined. We know $a_{k+1}$is $6\times a_k - 5\times a_{k+1}$ by definition. Inductive hypothesis is that P(i) is true for all 0≤i≤k, $a_i = 5^1 -1.$ Consider $a_{k+1} = 6\times(a_k)-5 \times a_{k-1}$ which is $6(5^k -1) - 5(5^{k-1}-1)$ (string induction). Therefore $a_{k+1} = 5^{k+1} -1$. $\forall n, a_n = 5^n -1$. Q.E.D.
Lesson 5: Recurrences
Looking at recursion.
Substitution Method:
Ex.
T(0) = 5 (base case)
T(n) = T(n-1) + n (next step)
How can we define T(n) without T?
- Recurrence relation
T(0) = 5
T(n) = T(n-1) + n
T(1) = T(0) + 1
T(3) = T(1) + 2 = T(0) 1 + 2
T(4) = T(2) + 3 = T(0) 1 + 2 + 3
T(5) = T(3) + 4 = T(0) 1 + 2 + 3 + 4
T(n) = T(0) + 1 + 2 + 3 …
$T(n) = T(0) + \frac{n(n+1)}{2} = 5 + \frac{n(n+1)}{2}$
Example 2:
T(1) = 1
T(n) = n + 2 * T(n/2)
$T(\frac{n}{2}) = \frac{n}{2} + 2\times T(\frac{n}{4})$
$T(n) = n+ 2( \frac{n}{2} + 2\times T(\frac{n}{4}))$
$T(\frac{n}{4}) = \frac{n}{4}+ 2\times T(\frac{n}{8})$
$T(\frac{n}{8}) = \frac{n}{8} + 2\times T(\frac{n}{16})$
$T(n) = n+2(\frac{n}{2} + 2(\frac{n}{4} + 2(\frac{n}{8} + 2\times T(\frac{n}{16}))))$
$T(n) = n+n+n+… 2^k\times T(\frac{n}{k})$
$T(n) = kn +2^k\times T(\frac{n}{k})$
Goal:
- No T’s on the right hand side
$T(1) = 1$ so what value of k does $T(\frac{n}{2^k}) = T(1)$
$\frac{n}{2^k} = 1$
$n = 2^k$
$\therefore k = log_2(n)$
$T(n) = n\times log_2 (n) + n$
Module 8 - Growth of Functions with Sorting
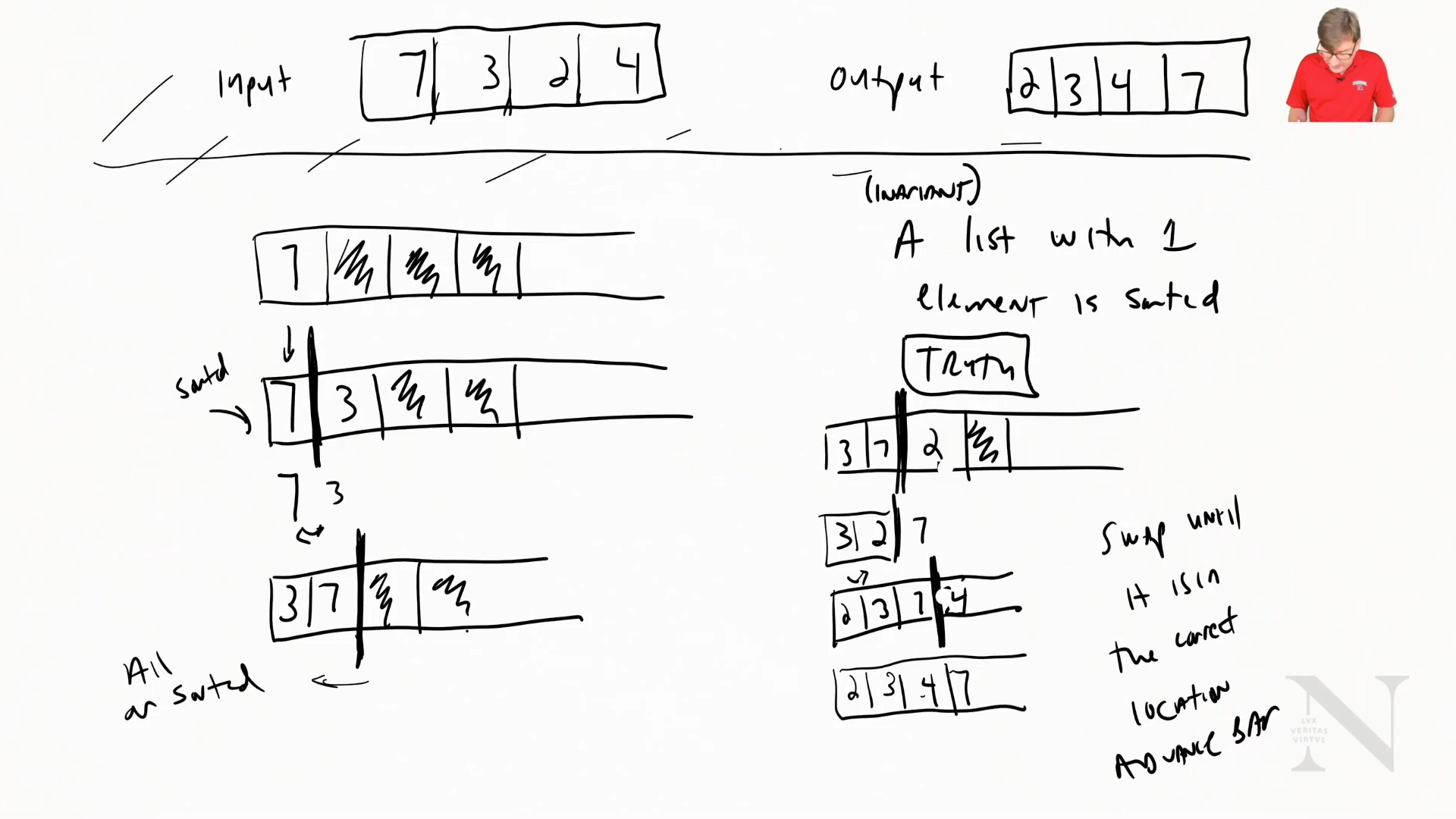
Lesson 1: Sorting a List of Number: Insertion Sort
We want to ask: How good are these sorting algorithms?
Input: 7,3,2,4 Output: 2,3,4,7
A list with one element is always sorted
This is an invariant which means that it is always true (never varies).
Insertion Sort:
- Swap until it is in the correct location
- Advance Bar
insertionSort(A)
for i from 1 to n-1:
current := A[i] // Current is one to insert
j := i-1 // Counter to end
while j>= 0 and A[j] > current:
swap(A[j], current)
j=j-1
How expensive is this?
Loop through every element -1
What doe sit do? Possible operations?
- Assignment
- Index into an array
- Subtraction
- Comparison
(These are called atomic operations)
A swap is 3 assignments
Atomic operations cost 1
- Any one thing that a computer does
We need to count the loop
- Worse case scenerio
for loop: n-1 iterations
while loop
- i=1 only 1 time
- i=2 most=2
- i=3 most=3
$\therefore$ Worst case: $\frac{(n-1)(n)}{2}$
Lesson 2: Sorting a List of Numbers: Merge Sort
Recall: a list of size 1 is already sorted
Merge Sort
- Take two lists and compare first element and remove the smaller one
Does long does this take?
- Worst case scenerio? (in terms of n)
2n comparisons to merge sorte lists
What we know:
- List of size 1 is sorted
- Merging list is “fast”
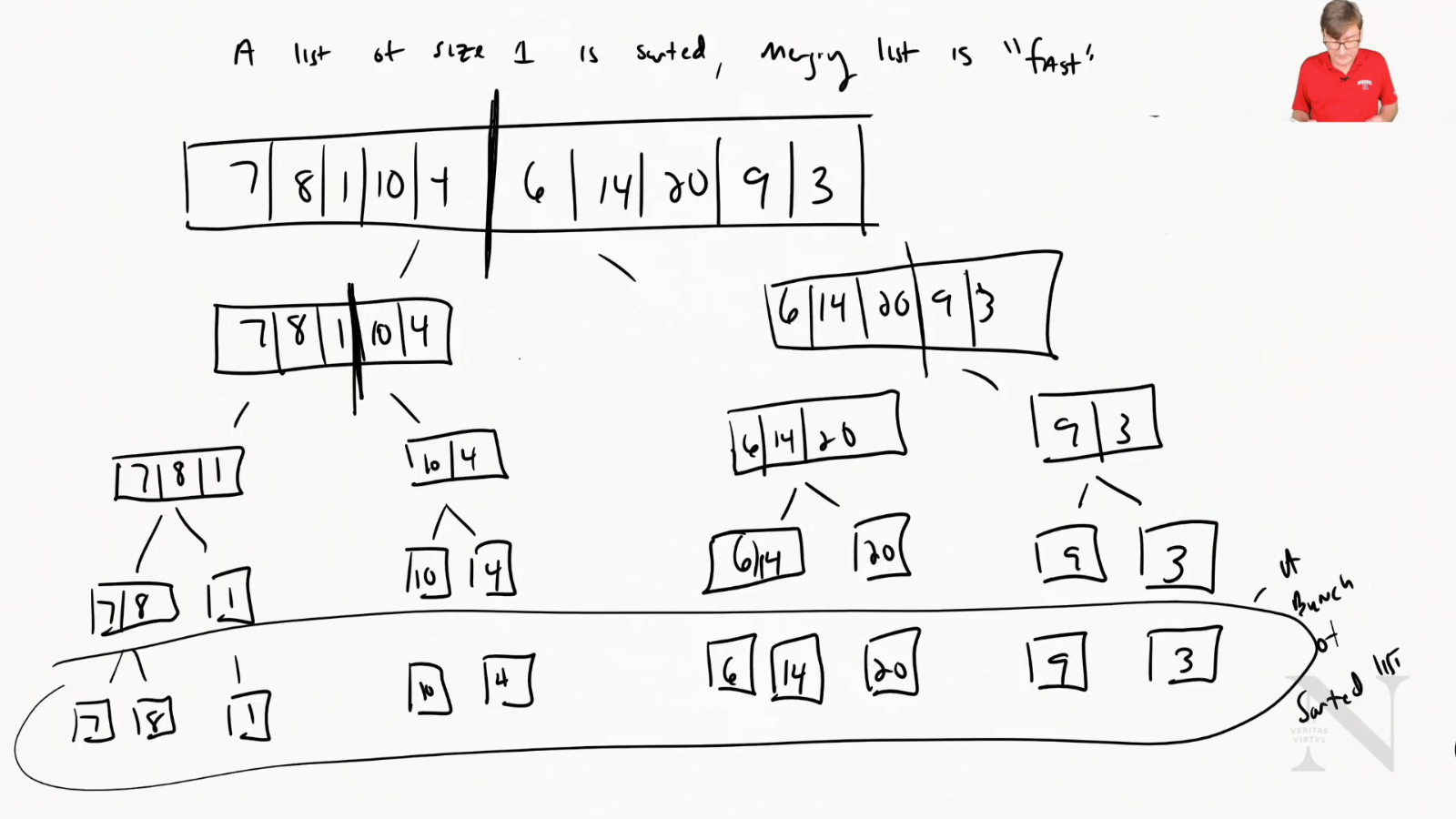
Now we can merge them quickly
Number of ways to have a number n is lg(n)
$\therefore \text{cost} = n\cdot lg(n)$
Code:
mergeSort(A, left, right)
if |A| > 1
middle = left + (right-left)/2
B = mergeSort(A, left, middle)
C = mergeSort(A, middle+1, right)
merge(B, C)
merge(A, B)
c = []
while (|A| > 0 and |B| > 0)
if (A[0] < B[0])
remove A[0] add to back of c
else
remove B[0] add to back of c
Is merge sort better than insertion sort? Yes!!
$\text{Merge Sort}: \approx n\cdot lg(n)$
$\text{Insertion Sort}: \frac{n(n-1)}{2} \approx n^2$
IMAGE:
![[Module 8 - Growth of Functions with Sorting/Screenshot_from_2020-12-01_21-04-43.png]]
Lesson 3: Asymptotic and Big O
Why can we say “about”?
We want to make algorithms efficent
We’re going ot focus on steps
- What is the growth rate of the change
Consider this code:
someFunc(A) //where |A| = n
n = |N| // Cost 2
while (n>0) //Cost 1
{
temp = x // Cost 2
x = y // Cost 1
y = temp // Cost 1
n = n - 1 // Cost 2
}
The total cost of this code is 7n+3
How different is 7n+3 and n when comparing function order?
- The gap is insignificant when we go to infinity
Big O Notiation
Classify function (group them) so we can compare them.
Let f(n) and g(n) be function mapping non-negative integers to real numbers.
f(n) is O(g(n)) if there exists a real constant c>0 and an integer $n_o >= 1$ such that $f(n) <= c\cdot g(n) \forall n >= n_o$
Claim: 7n+3 is O(n)
- They are the same class
Proof
Let c=8, then we konw that $7n+3<=8n$ for all $n>=3$. By the definition of Big O, 7n+3 is o(n).
Lesson 4: Ordering Functions
Big Omega
F(n) is $\Omega$(g(n)) if there exists a real constant c>0 and integer $n_o >=1$ such that $c\cdot g(n) <= f(n) \forall n >= n_o$
Big Theta
f(n) is $\Theta$(g(n)) if there exists constants $c_1>0,c_2>0\text{and} n_o >=1$ such that $c_1 \cdot g(n) <= f(n) <= c_2 \cdot g(n)$
$f(n) \text{is} O(g(n)) => f(n) <= g(n)$
$f(n) \text{is} \Omega(g(n)) => f(n) >= g(n)$
$f(n) \text{is} \Theta(g(n)) => f(n) = g(n)$
Little
f(n) is o(g(n)) if for all constants c>0, $\exists n_o > 0, f(n) < c\cdot g(n)\forall n >= n_o$
f(n) is $\omega(g(n))$ (little omega) if for all constants c>0, $\exists n_o >0, f(n) < c\cdot g(n) \forall n>= n_o$
f(n) is $\theta(g(n))$ (little theta) if for all constants c>0, $\exists n_o >0, c\cdot g(n) < f(n) \forall n>= n_o$
Size of Functions
In order of size:
constants, logs, polylogorithms, polynomials, exponential
Note: Exponential algorithms are not possible